- TI nspire
[TI-nspire] 지수 회귀 방정식, Exponential Regression
-
- 2024.10.24 - 19:42 2024.10.23 - 22:54 703 5
1. 실험 DATA
특정 미생물의 농도는 이론적으로 시간에 따라 다음 식과 같이 변한다고 한다.
$$ C = a \cdot \exp(-b \cdot t) = a \cdot e^{-b \cdot t}$$
실험에서 시간 \( t = 1 \)부터 \( t = 2.5 \)까지의 4개의 데이터 포인트에 대해 미생물 농도 \( C \) 값은 다음과 같다:
\[
\begin{array}{|c|c|}
\hline
t & C \\
\hline
1.0 & 6.05 \\
1.5 & 4.73 \\
2.0 & 3.69 \\
2.5 & 2.86 \\
\hline
\end{array}
\]
2. 회귀 방정식 (Regression)
주어진 식 \( C = a \cdot \exp(-b \cdot t) \)는 지수 함수 형태로, 지수적으로 감소하는 함수이기 때문에 이를 지수적 감소(exponential decay) 모델이라고 부르기도 합니다.
원래의 모형(공식)을 알고 있다면 그 모형과 가장 유사한 방식의 회귀 방정식을 선택하면 되고,
원래의 모형을 모르는 경우라면 데이터 값의 추세를 보고 결정해야 합니다.
위의 예에서는 (데이터 값이 적긴 하지만) 시간에 따라 자연적으로 감소하는 데이터의 형태를 보입니다.
예를 들어 방사성 붕괴나 미생물 성장/감소 등이 이러한 데이터 추세를 가집니다.
이러한 형태의 비선형 회귀 방정식을 지수 회귀 방정식(exponential regression)이라고 합니다.
실험 데이터를 바탕으로 지수 회귀 방정식의 \( a \)와 \( b \) 값을 추정하는 방법은 다음과 같은 단계를 따릅니다.
1. 양변에 자연 로그 취하기
주어진 식을 선형화하기 위해 양변에 자연 로그를 취합니다.
\[
\ln(C) = \ln(a) - b \cdot t
\]
즉, \( \ln(C) \)는 \( t \)에 대한 선형 함수가 됩니다:
\[
\ln(C) = -b \cdot t + \ln(a)
\]
이 식은 기울기가 \( -b \)이고, 절편이 \( \ln(a) \)인 직선 방정식입니다.
2. 데이터를 선형화
실험 데이터에서 \( t \)와 \( C \)의 값을 이용하여 \( \ln(C) \) 값을 계산합니다.
\[
\begin{array}{|c|c|c|}
\hline
t & C & \ln(C) \\
\hline
1.0 & 6.05 & \ln(6.05) = 1.800 \\
1.5 & 4.73 & \ln(4.73) = 1.554 \\
2.0 & 3.69 & \ln(3.69) = 1.306 \\
2.5 & 2.86 & \ln(2.86) = 1.051 \\
\hline
\end{array}
\]
3. 선형 회귀 분석
이제 \( \ln(C) \)와 \( t \)의 관계를 나타내는 선형 방정식의 기울기와 절편을 구하기 위해 선형 회귀 분석을 수행합니다. 선형 회귀는 다음과 같은 방정식을 사용합니다:
- 기울기 \( m \) (즉, \( -b \))는 다음과 같이 계산됩니다:
\[
m = \frac{n \sum t_i \ln(C_i) - \sum t_i \sum \ln(C_i)}{n \sum t_i^2 - (\sum t_i)^2}
\]
여기서:
- \( n = 4 \) (데이터 포인트의 개수)
- \( t_i \)와 \( \ln(C_i) \)는 주어진 데이터에서 가져옵니다.
데이터를 정리
\[
\begin{array}{|c|c|c|}
\hline
t_i & C_i & \ln(C_i) & t_i^2 & t_i \ln(C_i) \\
\hline
1.0 & 6.05 & 1.800 & 1.0 & 1.0 \cdot 1.800 = 1.800 \\
1.5 & 4.73 & 1.554 & 2.25 & 1.5 \cdot 1.554 = 2.331 \\
2.0 & 3.69 & 1.306 & 4.0 & 2.0 \cdot 1.306 = 2.612 \\
2.5 & 2.86 & 1.051 & 6.25 & 2.5 \cdot 1.051 = 2.628 \\
\hline
\end{array}
\]
각 합을 계산
이제 필요한 합들을 계산해보겠습니다:
1. \( \sum t_i = 1.0 + 1.5 + 2.0 + 2.5 = 7.0 \)
2. \( \sum \ln(C_i) = 1.800 + 1.554 + 1.306 + 1.051 = 5.711 \)
3. \( \sum t_i^2 = 1.0 + 2.25 + 4.0 + 6.25 = 13.5 \)
4. \( \sum t_i \ln(C_i) = 1.800 + 2.331 + 2.612 + 2.628 = 9.371 \)
기울기 \( m \) 계산
이제 이 값들을 공식에 대입해 \( m \)을 계산합니다.
\[
m = \dfrac{4 \cdot 9.371 - 7.0 \cdot 5.711}{4 \cdot 13.5 - 7.0^2} = -0.499
\]
- 절편 \( c \) 는 다음과 같이 계산됩니다:
\[
c = \frac{\sum \ln(C_i) - m \sum t_i}{n}
\]
여기에 이미 계산된 값을 대입해보겠습니다:
- \( \sum \ln(C_i) = 5.711 \)
- \( m = -0.499 \)
- \( \sum t_i = 7.0 \)
- \( n = 4 \)
$$ \text{절편 } c = \dfrac{5.711 - (-0.499 \times 7.0)}{4} = 2.301 $$
선형 회귀 방정식
$$ y = mx+c = -0.499 \cdot t + 2.301 $$
4. 지수 회귀 방정식으로 전환 : \( a \)와 \( b \) 구하기
선형 회귀 방정식에서 구한
기울기 \( m = -0.499\)이 \( -b \)이므로, 이를 이용해 \( b = 0.499\) 값을 구할 수 있고,
절편 \( c = ln(a \cdot e^{t})|_{t=0} = \ln(a) \)이므로, 이를 이용해 \( a \) 값을 구할 수 있습니다:
\( a \)는 이 값의 자연 로그 역함수이므로, \( a = \exp(2.301) \approx 9.98 \)입니다.
위 과정을 통해 최종적으로 지수 회귀 방정식을 구하였습니다.
$$ C = 9.98 \cdot \exp(-0.499 \cdot t) = 9.98 \cdot e^{-0.499 \cdot t} $$
3. TI-nspire 의 활용
기본 데이터 값의 입력 및 계산
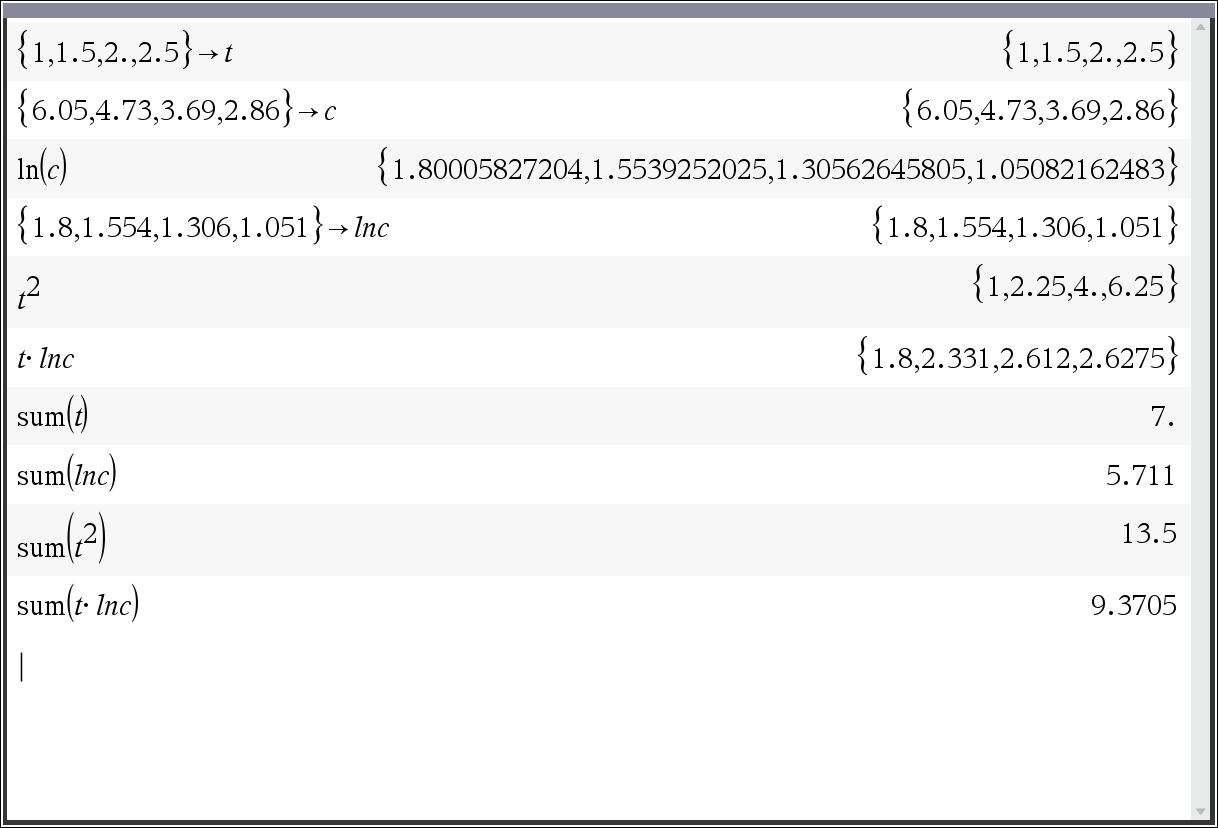
ln(c) 의 선형 회귀 계산
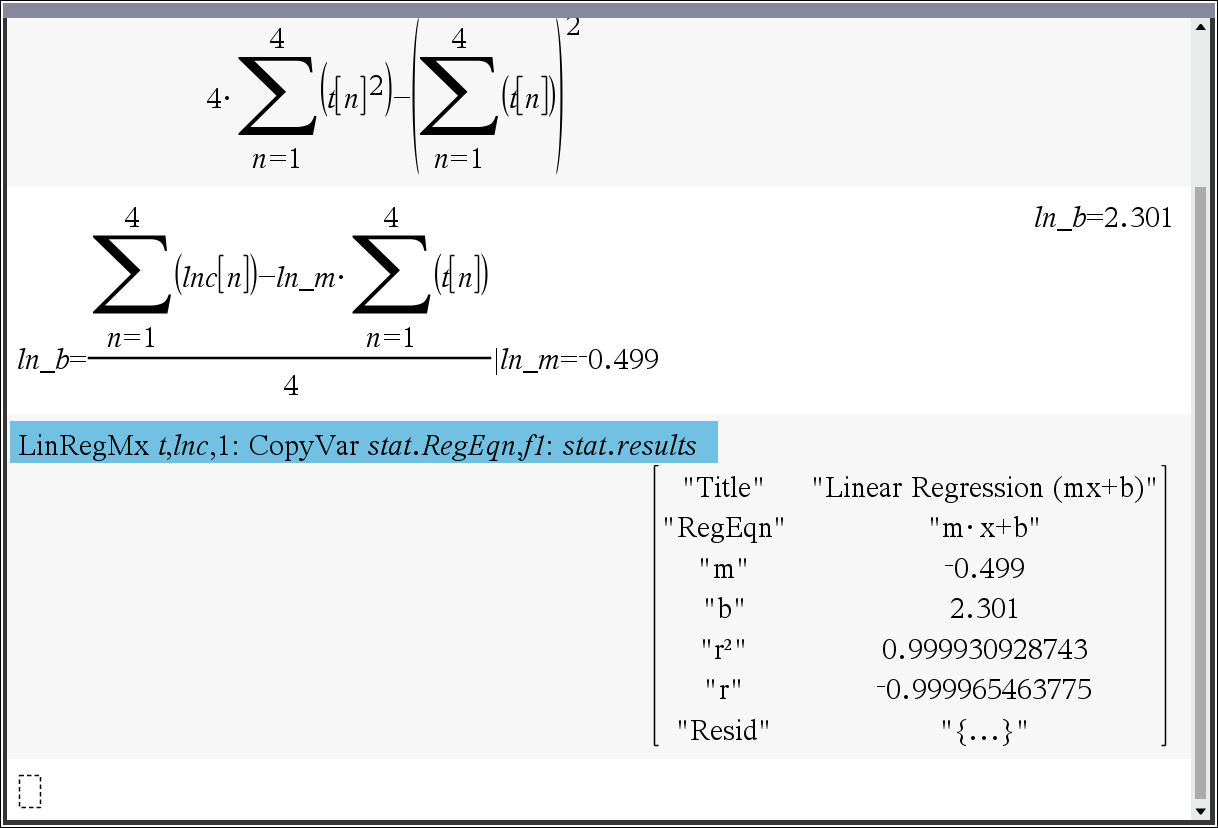
ㄴ ∑ 함수를 말고 sum() 함수에 list 변수를 넣어서 계산하면 간단합니다.
ㄴ 여기서는 단지 공식을 표현하기 위해 사용한 것 뿐입니다.
지수 회귀 직접 계산
: 공학용 계산기에는 지수 회귀 방정식 기능이 있기 때문에 앞서 ln(c)를 선형회귀하는 과정이 불필요합니다.
그런데
구해진 TI-nspire 의 지수 회귀 방정식은 $ y = a \cdot e^{-b \cdot t} $ 꼴이 아니고,
$ y = a \cdot b^{t} $ 꼴이기 때문에 마지막으로 한번 더 계산이 필요합니다.
ㄴ solve 또는 ln() 으로 간단하게 찾을 수 있습니다.
한번에 찾을 방법은
(현재 기본 기능만으로는) DataQuest 앱을 이용하는 방법 뿐입니다. : 댓글 참고
불편하면 프로그램(라이브러리)를 만들어야겠죠.
-
25
댓글5
-
세상의모든계산기
최소자승법(최소 제곱법, Least Squares Method)을 행렬로 푸는 방법은 다음과 같은 수식을 사용합니다:
\[
\hat{\beta} = (A^T A)^{-1} A^T y
\]여기서:
- \( A \)는 독립 변수 \( t \)의 행렬
- \( y \)는 종속 변수 \( \ln(C) \)의 벡터
- \( \hat{\beta} \)는 구하려는 계수 벡터로, 기울기 \( b \)와 절편 \( \ln(a) \)가 들어갑니다.1. 행렬 \( A \), \( y \) 정의
주어진 데이터에서 \( t \)와 \( \ln(C) \) 값을 이용하여 다음과 같이 행렬 \( A \)와 벡터 \( y \)를 정의할 수 있습니다:# 데이터:
\[
\begin{array}{|c|c|}
\hline
t & \ln(C) \\
\hline
1.0 & 1.800 \\
1.5 & 1.554 \\
2.0 & 1.306 \\
2.5 & 1.051 \\
\hline
\end{array}
\]행렬 \( A \)는 상수항(절편)을 포함하기 위해 \( 1 \)을 추가하여 다음과 같이 구성됩니다:
\[
A = \begin{pmatrix}
1 & 1.0 \\
1 & 1.5 \\
1 & 2.0 \\
1 & 2.5
\end{pmatrix}
\]벡터 \( y \)는 종속 변수인 \( \ln(C) \) 값을 사용하여 구성됩니다:
\[
y = \begin{pmatrix}
1.800 \\
1.554 \\
1.306 \\
1.051
\end{pmatrix}
\]2. \( A^T A \) 계산
행렬 \( A^T \)는 \( A \)의 전치 행렬이므로 다음과 같습니다:\[
A^T = \begin{pmatrix}
1 & 1 & 1 & 1 \\
1.0 & 1.5 & 2.0 & 2.5
\end{pmatrix}
\]이제 \( A^T A \)를 계산합니다:
\[
A^T A = \begin{pmatrix}
1 & 1 & 1 & 1 \\
1.0 & 1.5 & 2.0 & 2.5
\end{pmatrix}
\begin{pmatrix}
1 & 1.0 \\
1 & 1.5 \\
1 & 2.0 \\
1 & 2.5
\end{pmatrix}
\]\[
A^T A = \begin{pmatrix}
4 & 7.0 \\
7.0 & 13.5
\end{pmatrix}
\]3. \( A^T y \) 계산
다음으로 \( A^T y \)를 계산합니다:\[
A^T y = \begin{pmatrix}
1 & 1 & 1 & 1 \\
1.0 & 1.5 & 2.0 & 2.5
\end{pmatrix}
\begin{pmatrix}
1.800 \\
1.554 \\
1.306 \\
1.051
\end{pmatrix}
\]\[
A^T y = \begin{pmatrix}
1.800 + 1.554 + 1.306 + 1.051 \\
1.0 \cdot 1.800 + 1.5 \cdot 1.554 + 2.0 \cdot 1.306 + 2.5 \cdot 1.051
\end{pmatrix}
\]\[
A^T y = \begin{pmatrix}
5.711 \\
9.371
\end{pmatrix}
\]4. 계수 벡터 \( \hat{\beta} \) 계산
이제 계수 벡터 \( \hat{\beta} \)는 다음과 같이 구할 수 있습니다:\[
\hat{\beta} = (A^T A)^{-1} A^T y
\]먼저 \( A^T A \)의 역행렬을 구합니다:
\[
(A^T A)^{-1} = \frac{1}{(4 \cdot 13.5 - 7.0^2)} \begin{pmatrix} 13.5 & -7.0 \\ -7.0 & 4 \end{pmatrix}
\]\[
(A^T A)^{-1} = \frac{1}{5.0} \begin{pmatrix} 13.5 & -7.0 \\ -7.0 & 4 \end{pmatrix}
\]\[
(A^T A)^{-1} = \begin{pmatrix} 2.7 & -1.4 \\ -1.4 & 0.8 \end{pmatrix}
\]이제 역행렬과 \( A^T y \)를 곱하여 \( \hat{\beta} \)를 구합니다:
\[
\hat{\beta} = \begin{pmatrix} 2.7 & -1.4 \\ -1.4 & 0.8 \end{pmatrix} \begin{pmatrix} 5.711 \\ 9.371 \end{pmatrix}
\]\[
\hat{\beta} = \begin{pmatrix} (2.7 \cdot 5.711) + (-1.4 \cdot 9.371) \\ (-1.4 \cdot 5.711) + (0.8 \cdot 9.371) \end{pmatrix}
\]계산하면:
\[
\hat{\beta} = \begin{pmatrix} 15.4197 - 13.1194 \\ -7.9954 + 7.4968 \end{pmatrix}
\]\[
\hat{\beta} = \begin{pmatrix} 2.3003 \\ -0.4986 \end{pmatrix}
\]5. 결과
따라서, \( \hat{\beta} = \begin{pmatrix} 2.3003 \\ -0.4986 \end{pmatrix} \), 이는 다음을 의미합니다:
- 절편 \( \ln(a) \approx 2.3003 \), 따라서 \( a = \exp(2.3003) \approx 10.0 \)
- 기울기 \( b \approx 0.4986 \)이 방법을 통해 \( a \)와 \( b \) 값을 행렬 계산을 사용하여 구할 수 있습니다.
-
1
-
세상의모든계산기
fx-570 을 이용한 계산 방법
https://allcalc.org/51166
* fx-570 에는 e^X 꼴, A*B^X 꼴 둘 다 있어서 한번에 되는데...
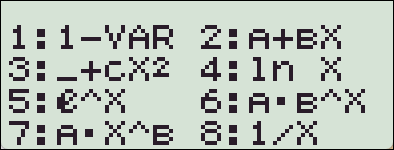
왜 TI-nspire 에는 왜 하나만 있지?
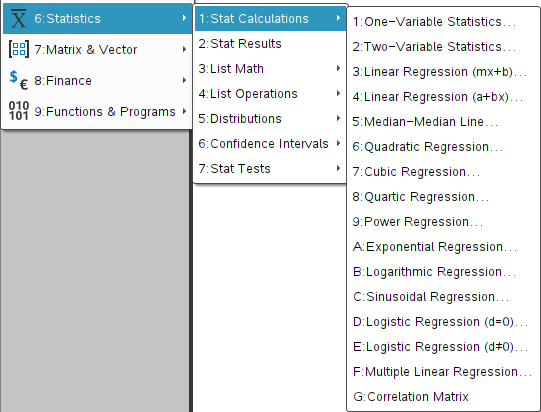
있는데 방법을 모르는 것 뿐인가?
-
1
세상의모든계산기
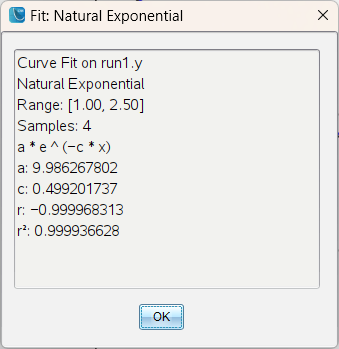
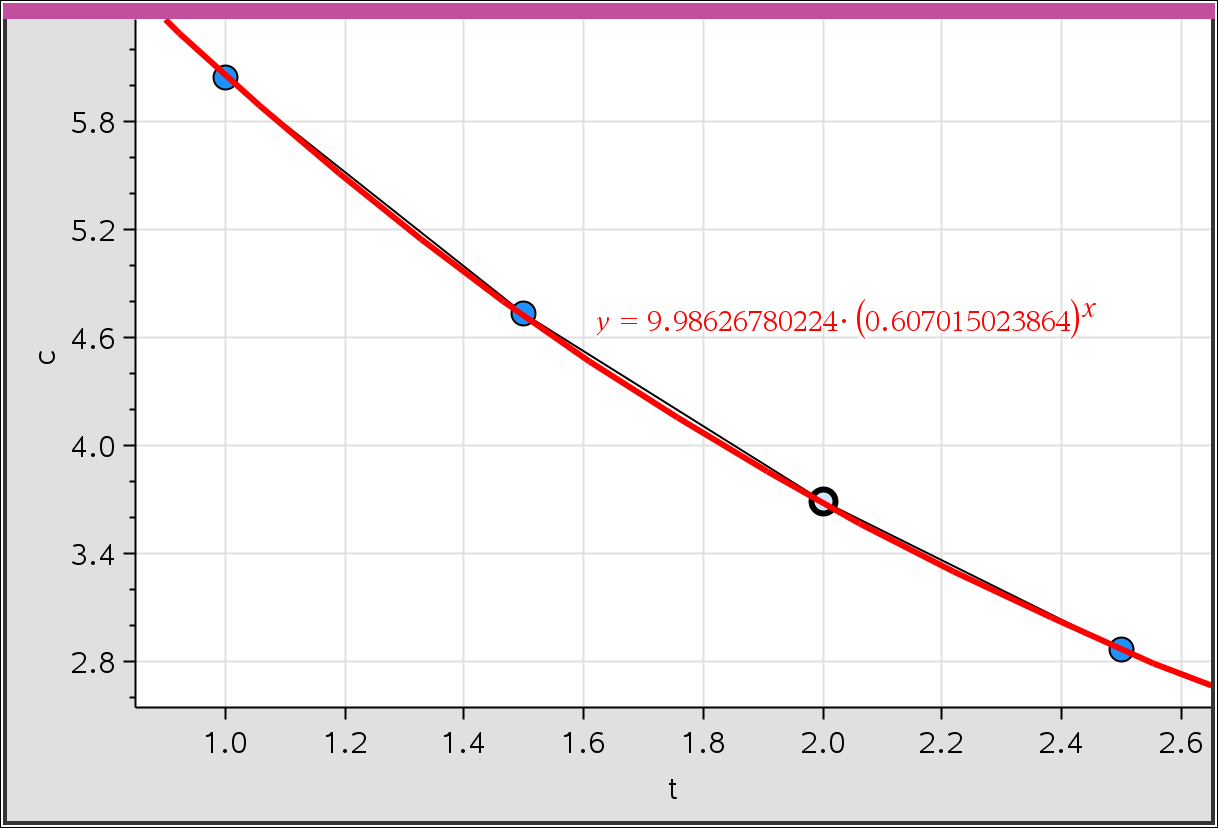
vernier DataQuest 앱에는 해당 기능이 있습니다. Natural exponential Regression
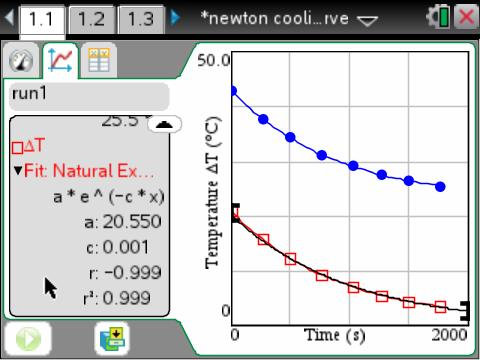
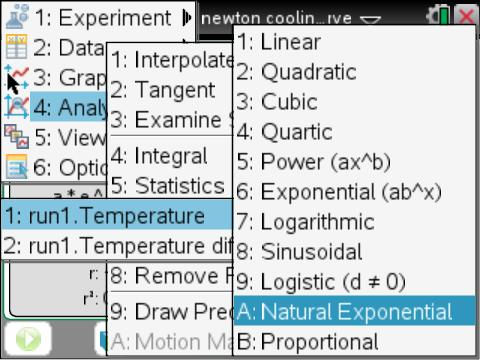
출처 : https://groups.google.com/g/tinspire/c/97sKKp8WVB0
보니까 직접 실험장치를 통해 얻은 데이터만 쓸 수 있는게 아니고,
계산기에 입력된 리스트값도 링크해서 쓸 수 있네요. Link from List
-
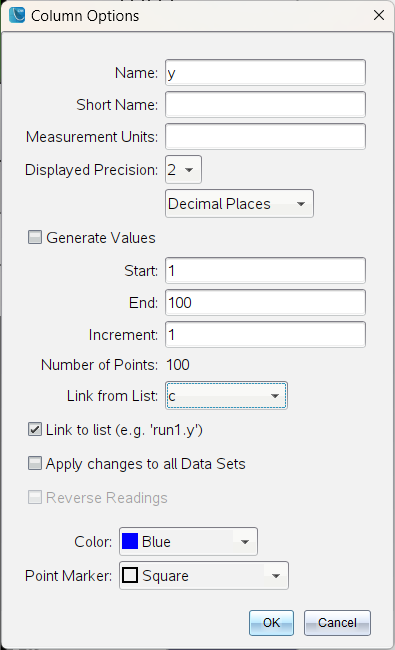
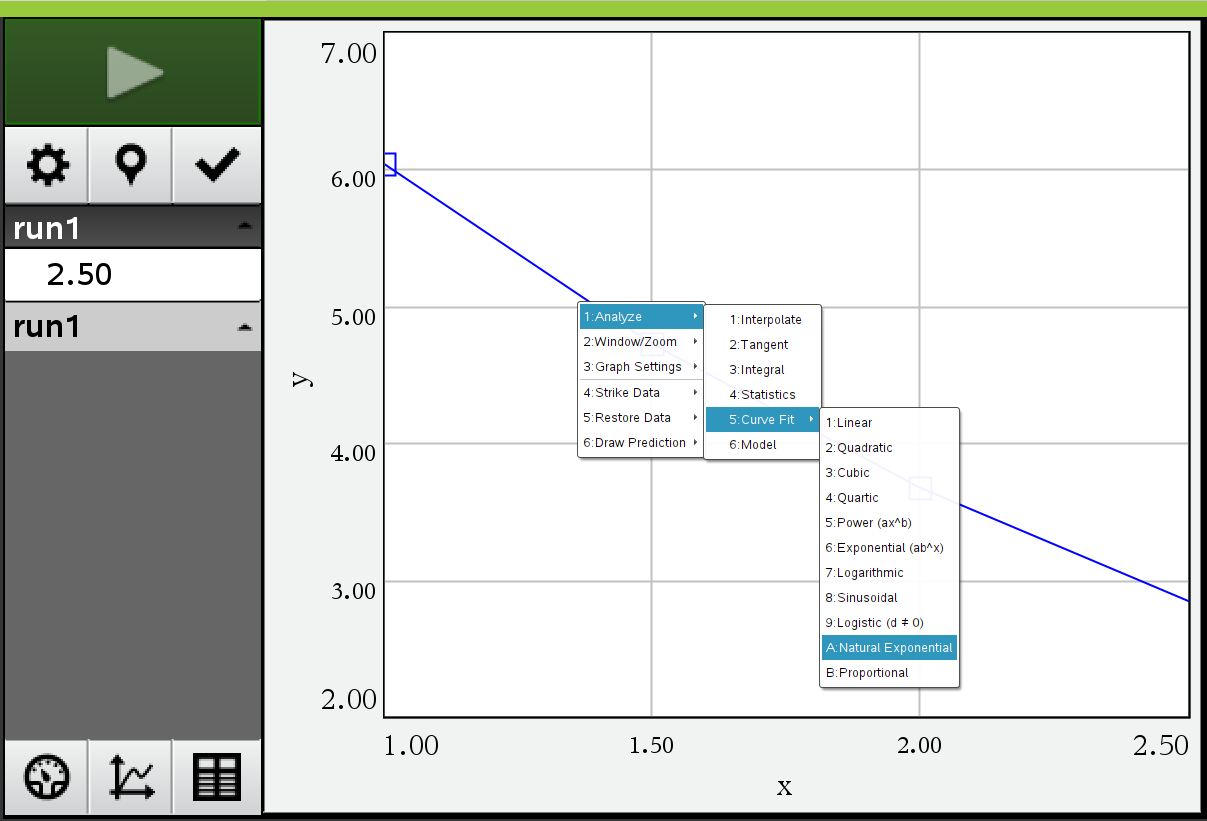
세상의모든계산기 님의 최근 댓글
V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04 1. 분모 먼저 계산 400 × 10000 = 100 × 6000 = GT 결과값 4,600,000 역수 처리 ÷÷== 결과값 0.00000021739 2. 분자 곱하기 ×3 00 00 00 ×4 00 ×1 00 00 최종 결과 = 2,608,695.65217 2026 02.04 해결 방법 1. t=-1 을 기준으로 그래프를 2개로 나누어 표현 ㄴ 근데 이것도 tstep을 맞추지 않으면 문제가 발생할 것기도 하고, 상관이 없을 것 같기도 하고... 모르겠네요. 2. t=-1 이 직접 계산되도록 tstep을 적절하게 조정 tstep=0.1 tstep=0.01 도 해 보고 싶지만, 구간 크기에 따라 최소 tstep 이 변하는지 여기서는 0.01로 설정해도 0.015로 바뀌어버립니다. 그래서 tstep=0.02 로 하는게 최대한 긴 그래프를 얻을 수 있습니다. 2026 02.02 불연속 그래프 ti-nspire는 수학자처럼 연속적인 선을 그리는 것이 아니라, 정해진 `tstep` 간격으로 점을 찍고 그 점들을 직선으로 연결하는 'connect-the-dots' 방식으로 그래프를 그립니다. 여기에 tstep 간격에 따라 특이점(분모=0)이 제외되어 문제가 나타난 것입니다. seq(−2+0.13*t,t,0,23) {−2.,−1.87,−1.74,−1.61,−1.48,−1.35,−1.22,−1.09,−0.96,−0.83,−0.7,−0.57,−0.44,−0.31,−0.18,−0.05,0.08,0.21,0.34,0.47,0.6,0.73,0.86,0.99} t=-1 에서 그래프를 찾지 않습니다. 그 좌우 값인 −1.09, −0.96 두 값의 그래프값을 찾고, Window 범위를 보고 적당히 (연속되도록) 이어서 그래프를 완성하는 방식입니다. 그래서 t=-1에서도 그래프 값이 존재하는 것입니다. 2026 02.02