- TI nspire
[TI-nspire] 경고 문구 설명 Warning : Domain of the result might be larger than the domain of the input.
1. TI-nspire의 경고 문구는?
TI-nspire 에서 계산을 하다보면
수식 앞에 삼각형(느낌표)표시  가 뜨면서 결과가 표시될 때가 종종 있습니다.
가 뜨면서 결과가 표시될 때가 종종 있습니다.
터치패드를 이용해 손가락(커서)을 띄우고 느낌표에 가져다 대면 상세 경고 문구를 확인할 수 있습니다.
https://education.ti.com/html/webhelp/eg_tinspire/en/Subsystems/EG_RefGuide/Content/M_RefGuide/RG_Warning_Codes_and_Messages.HTML
경고 코드는 위 링크에서 찾아볼 수 있는 것처럼 다양하지만, 우리가 계산기를 사용하면서 주로 보게되는 것은 몇가지 뿐입니다.
※ 경고문구가 이렇게 다양한 이유는 근본적으로는 CAS기능이 있기 때문이라고 볼 수 있습니다.
이 글에서는 가장 흔하게 나타나는 경고 문구 중 하나인
"Domain of the result might be larger than the domain of the input."에 대해 살펴 보겠습니다.
2. domain 이란?
"Domain"은 수학에서 함수가 정의되는 입력 값의 범위를 의미합니다.
수학시간에 들었던 용어로 바꾸면 "정의역" 이 됩니다.
ㄴ Domain의 사전적 정의 : an area of interest or an area over which a person has control. 일본말로는 "나와바리"?
도메인은 해 자체를 의미하는 것은 아니고, 특정 함수나 식에서 해가 될 수 있는 입력 값의 가능 범위를 뜻합니다.
예를 들어 분수함수 \( f(x) = \dfrac{1}{x} \) 에서 분모는 0이 될 수 없기 때문에, 함수의 도메인은 \( x \neq 0 \)인 모든 실수입니다.
3. 에러의 예시
1) 분모 ≠ 0
아주 간단한 예를 들어 보겠습니다. $ \dfrac{x}{x} = 1 $

좌측(Input) 은 x≠0 일 때만 정의되고, 결과값은 항상 1입니다.
우측(output) 은 x와 관계 없이 항상 1 입니다.
우측은 x≠0 조건이 없어지면서 도메인이 실수 전체(R) 로 확장되었기 때문에, 경고를 하는 것입니다.
Result domain 이 Input domain 보다 더 클 수 있다
= 결과값은 제약(조건)이 부족할 수 있다.
= 결과값을 그대로 이용하지 말고, 조건에 항상 신경을 써야 한다.
이렇게 이해하시면 될 듯 합니다.
다른 예 ) $ \frac{a}{b} \left\lvert\, a=\frac{c}{d}\right. \text { and } b=\frac{e}{f} $

Domain of Input (입력 정의역)
1. \(\dfrac{a}{b}\)의 정의역:
- \( b \neq 0 \) 이어야 합니다. \( b \)가 분모로 사용되기 때문입니다.
2. \(\dfrac{c}{d}\)의 정의역:
- \( d \neq 0 \) 이어야 합니다.
3. \( b = \dfrac{e}{f}\)의 정의역:
- \( f \neq 0 \) 이어야 합니다. \( f \)가 분모로 사용되기 때문입니다.
따라서, 주어진 입력 식에서 정의역은 다음과 같습니다:
\[
d \neq 0 \quad \text{and} \quad f \neq 0 \quad \text{and} \quad e \neq 0
\]
Domain of Result (결과 정의역)
계산기에서 제공한 결과는 \(\dfrac{c \cdot f}{d \cdot e}\)로, 정의역은 다음과 같습니다:
\[
d \cdot e \neq 0 \quad
\]
이는 다음과 같이 조건을 세분화할 수 있습니다:
1. \( d \neq 0 \): 분모에 \( d \)가 있으므로 필요합니다.
2. \( e \neq 0 \): 분모에 \( e \)가 있으므로 필요합니다.
Input 정의역과 Result 정의역 비교
Input 정의역: \( d \neq 0 \), \( f \neq 0 \), \( e \neq 0 \)
Result 정의역: \( d \neq 0 \), \( e \neq 0 \) (조건 \( f \neq 0 \) 이 사라지면서 범위가 확장)
변수 간의 종속성을 유지한다면 \( f \neq 0 \) 역시도 domain 조건에 포함되어야 하겠으나,
계산기 결과식에는 그러한 종속성 조건이 따라붙지 않기 때문에,
사용자가 주의하지 않고 결과식만을 가져다가 이용한다면 f=0 라는 불가능한 조건을 사용하면서 최종 결과에 문제를 발생시킬 수 있습니다.
2) 함수가 가진 본래의 정의역이 있는 경우
https://allcalc.org/32601
$ \sin \left( \sin ^{-1}\left( \theta \right) \right) =\theta $
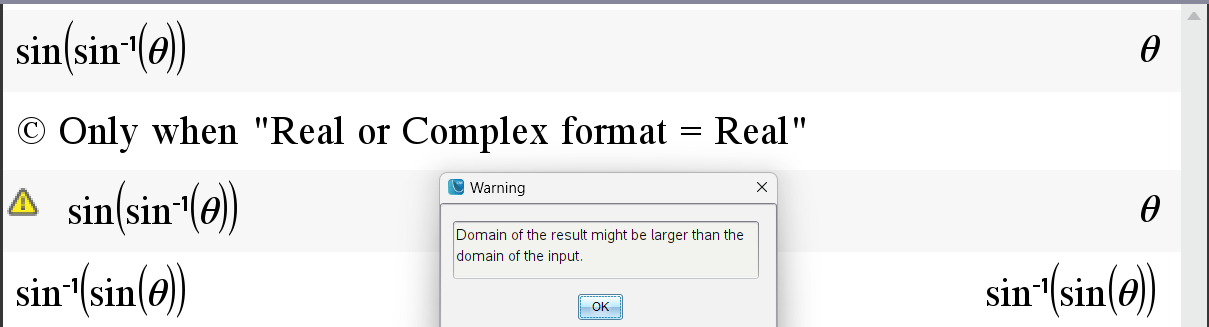
서로 역함수 관계인 두 함수를 연속으로 사용하면, 서로 상쇄되기 때문에 처음의 인수인 θ 가 그대로 튀어나오는게 맞죠.
하지만 입력쪽의 arcsin 함수는 정의역 구간이 따로 정의되어 있습니다. $ -\dfrac{\pi }{2}\leqq x\leqq \dfrac{\pi }{2} $
출력쪽의 θ에는 그러한 정의역 구간이 사라지면서 실수(R) 전체로 확장되었기 때문에 경고를 주는 것입니다.
3) 루트가 포함된 결과에서
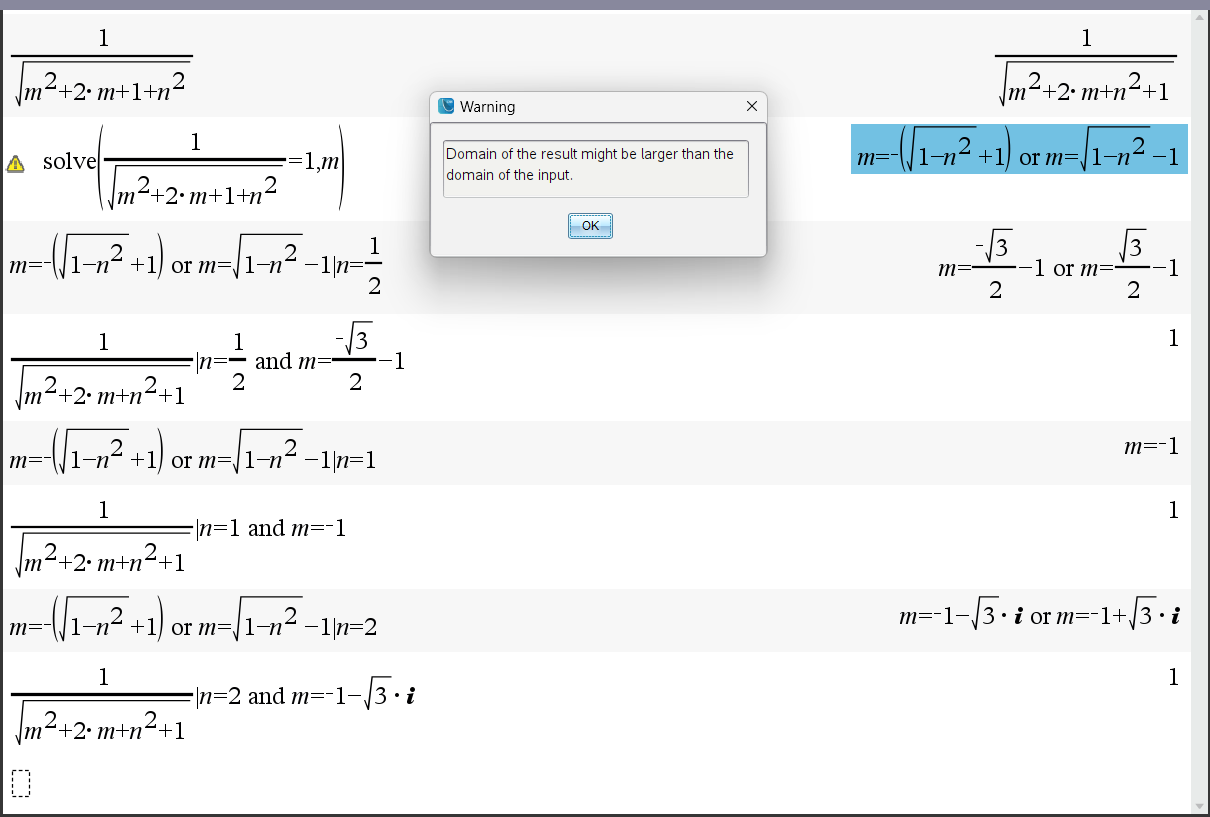
두번째 solve( ) 결과로 찾아진 수식에서 경고가 뜬 것은
|n|>1 일 때 m이 복소수가 되기 때문입니다. 즉 결과값의 Domain 이 복소수 도메인 (\(\mathbb{C}\)) 로 확장되었음을 알 수 있습니다.
이것이 원래 의도한 것일 수도 있지만, 의도하지 않은 것일 수도 있기 때문에 경고를 주는 것입니다.
4) 복소수 변수 지정 vs 미지정

여기서 확인할 수 있는 것
- "수식에 해가 존재하는가? 존재하지 않는가?" 에 관계 없이, 변수를 복소수로 지정(x_)하지 않으면 경고가 발생
- 분모≠0 인 조건 때문에 경고가 발생했다고 보긴 어렵습니다. Input / Output 모두 그 조건에 의해 제약되는 범위는 x≠0 로 같기 때문입니다.
그럼 왜 경고가 나온 걸까요?
Input 쪽의 x는 실수 도메인 (\(\mathbb{R}\)) 으로 인식되었고, Output 쪽의 x는 (비록 같은 모양이지만) 복소수 도메인 (\(\mathbb{C}\)) 으로 확장되어 인식되었기 때문입니다.
앞에서 살펴본대로 사용자가 모르고 사용하는 것을 경고하는 것이구요.
x_ 를 지정함으로서 "도메인이 복소수인거 알고있어!" 라고 하면 경고를 하지 않는 것이죠.
댓글1
-
세상의모든계산기
TI-Nspire의 경고 문구가 다양한 이유는 CAS(Computer Algebra System) 기능이 내장되어 있기 때문입니다.
CAS는 수학적 계산과 관련된 다양한 상황을 처리할 수 있는 강력한 도구로, 아래와 같은 방식으로 경고 문구와 관련이 있습니다.
1. 복잡한 계산 처리
CAS는 비선형 방정식, 미분, 적분, 함수의 해를 찾는 등의 복잡한 계산을 수행할 수 있습니다. 이러한 과정에서 발생할 수 있는 다양한 문제를 인지하고, 이를 사용자에게 경고하기 위해 다양한 메시지를 제공합니다.예를 들어, "Operation might introduce false solutions"와 같은 경고는 사용자가 입력한 식이 정확한 해를 찾지 못할 가능성을 시사합니다.
2. 해의 신뢰성 검증
CAS는 복잡한 해를 도출할 때, 해당 해가 신뢰할 수 있는지 여부를 평가합니다."Questionable solution" 또는 "Questionable accuracy"와 같은 메시지는 결과의 정확성이나 신뢰성이 불확실할 때 발생합니다.
이는 사용자가 결과를 그래픽적으로 확인하도록 유도하여, 결과의 올바름을 스스로 검증할 수 있게 합니다.
3. 도메인 검증
CAS는 입력값과 결과값의 도메인을 명확히 분석합니다.예를 들어, "Domain of the result might be smaller than the domain of the input"과 같은 경고는 입력값이 정의된 범위에서 결과값이 유효하지 않을 수 있음을 알립니다.
이는 사용자가 특정 입력에 대해 결과를 사용할 때 주의해야 함을 의미합니다.
4. 해의 다양성 인지
CAS는 여러 해가 존재할 수 있는 경우를 인식하여 경고합니다."More solutions may exist"와 같은 메시지는 사용자가 결과를 도출할 때 더 많은 해가 있을 수 있음을 알려줍니다.
이는 사용자가 해의 존재 범위를 명확히 이해하고, 추가적인 해를 찾도록 유도하는 역할을 합니다.
5. 정확도와 근사값 처리
CAS는 수치적 계산에서 발생할 수 있는 오차와 근사값을 관리합니다."Result obtained using approximate arithmetic"와 같은 경고는 계산이 근사값을 사용하여 이루어졌음을 알려주어, 사용자가 그 결과에 대해 주의를 기울이도록 합니다.
6. 특정 조건 인식
CAS는 다양한 조건과 제약을 이해하고 이를 바탕으로 경고를 발행합니다.예를 들어, "Input contains an undefined parameter" 경고는 입력값에 정의되지 않은 변수가 포함되어 결과가 유효하지 않을 수 있음을 나타냅니다. 이는 사용자가 명확한 조건을 명시하도록 유도합니다.
7. 상대적인 연산 조건
CAS는 연산이 특정 조건을 만족해야 함을 인지하고, 조건을 충족하지 않을 경우 경고를 발생시킵니다.예를 들어, "Operation requires and returns 64 bit value"는 특정 연산이 64비트 값의 처리를 요구할 때 발생하는 경고입니다.
이와 같이 TI-Nspire의 경고 문구는 CAS 기능이 수학적 계산을 수행하면서 발생할 수 있는 다양한 문제를 사용자가 미리 인지하고 대응할 수 있도록 도와주는 역할을 합니다.
이를 통해 사용자는 보다 신뢰할 수 있는 계산 결과를 얻고, 잠재적인 오류를 예방할 수 있습니다.


세상의모든계산기 님의 최근 댓글
[fx-570 ES] 과학 상수를 이용한 계산에서 에러 발생 상황 https://kin.naver.com/qna/detail.naver?d1id=11&dirId=1118&docId=492235162&page=1&answerNo=1 vs 2026 03.01 과학상수를 이용한 계산 중 자릿수 한계로 인한 에러 발생 가능성 https://allcalc.org:443/board_calculators/6925#comment_57029 2026 03.01 기본 어댑터 MODEL : AD0301-1202500GB INPUT : 100~240V, 50~60Hz, 0.8A Max OUTPUT : 12.0V, 2.5A, 30.0W ㄴ 측정시 플러그 외경/내경 : 5.5mm / 2mm 2026 02.15 엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10 엑셀 / 행의 최대 개수, 열의 최대 개수, 셀의 최대 개수 엑셀의 행 개수 제한은 파일 형식에 따라 다르며, 최신 .xlsx 파일 형식은 시트당 최대 1,048,576행까지 지원하지만, 구형 .xls 파일은 65,536행으로 제한됩니다. 따라서 대용량 데이터를 다룰 때는 반드시 최신 파일 형식(.)으로 저장해야 하며, 행과 열의 총 수는 1,048,576행 x 16,384열이 최대입니다. 주요 행 개수 제한 사항: 최신 파일 형식 (.xlsx, .xlsm, .xlsb 등): 시트당 1,048,576행 (2^20). 구형 파일 형식 (.xls): 시트당 65,536행 (2^16). 그 외 알아두면 좋은 점: 최대 행 수: 1,048,576행 (100만여개) 최대 열 수: 16,384열 (XFD) 대용량 데이터 처리: 65,536행을 초과하는 데이터를 다루려면 반드시 .xlsx 형식으로 저장하고 사용해야 합니다. 문제 해결: 데이터가 많아 엑셀이 멈추거나 오류가 발생하면, 불필요한 빈 행을 정리하거나 Inquire 추가 기능을 활용하여 파일을 최적화할 수 있습니다. 2026 02.10