샤프 계산기(EL-W506T, EL-5500X 등) 정적분 계산시 오차 주의 - 정적분 정밀도 높이기
1. 미스터리: 같은 문제, 두 개의 다른 답
공학용 계산기는 복잡한 수학 문제를 해결하는 강력한 도구입니다. 하지만 때로는 우리를 당황하게 만들기도 합니다.
특정 Sharp 공학용 계산기 모델에서 다음 정적분 문제를 계산했을 때, 설정 하나 차이로 전혀 다른 두 결과가 나오는 현상이 발견되었습니다.
문제: ∫(1 / ((1-x)(2-x))) dx 를 0부터 0.999까지 적분하시오.
- 기본 설정으로 계산한 결과:
6.747063684
- 계산식 마지막에
,1000을 추가하여 수동 설정으로 계산한 결과:6.217014664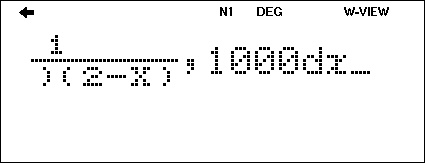

어째서 이런 큰 차이가 발생했을까요? 이 글에서는 그 원인을 파헤치고, 계산기를 더 정확하게 사용하는 방법을 안내합니다.
2. 원인 분석: 공학용 계산기는 어떻게 정적분을(넓이를) 구하는가?
가. 진짜 정답: 해석적 방법 = 사람이 하는 방법 = CAS 계산기가 하는 방법
오차를 알기 위해선 먼저 '참값'을 알아야 합니다. 이 문제는 부분분수 분해를 통해 수학적으로 정확하게 풀 수 있습니다.
1 / ((1-x)(2-x))는 1/(1-x) - 1/(2-x)와 같습니다. 이를 적분하면 ln|(2-x)/(1-x)|가 되며, 0부터 0.999까지 정적분한 참값은 ln(500.5) 입니다.
고정밀도 계산기로 구한 참값은 약 6.2156075987... 입니다.
나. 계산기의 방식: 수치 적분과 '구간'
계산기는 사람처럼 수식을 푸는 것이 아니라, 수치 적분이라는 근사적인 방법으로 넓이를 구합니다.
마치 곡선 아래 영역을 수많은 잘게 썬 '피자 조각(구간)'으로 나누고, 각 조각의 넓이를 더하는 것과 같습니다.
Sharp 계산기는 별도 설정이 없으면 이 조각의 개수, 즉 구간(subinterval)을 100개로 하여 계산합니다. (*설명서 참고)
다. 무엇이 오차를 만들었나?
이제 모든 조각이 맞춰졌습니다. 계산 결과를 표로 비교해 보겠습니다.
| 계산 방식 | 구간(Subinterval) 수 | 결과값 | 참값과의 차이 (오차) |
|---|---|---|---|
| 참값 (ln(500.5)) | - | 6.215607... | - |
| Sharp (기본 설정) | 100 | 6.747063... | 약 +0.531 (매우 큰 오차) |
| Sharp (수동 설정) | 1000 | 6.217014... | 약 +0.0014 (오차 대폭 감소) |
오차의 핵심 원인은 적분하려는 함수 f(x)가 x=1에서 분모가 0이 되어 값이 무한대로 치솟는 '수직 점근선'을 가지기 때문입니다.
적분 구간의 끝인 0.999는 이 위험 지점 바로 옆입니다.
- 100 구간 (실패): 구간의 폭이 너무 넓어서,
x=0.99에서x=0.999사이의 폭발적인 값의 증가를 제대로 감지하지 못하고 건너뛰어 버립니다. 결국 엉뚱한 넓이를 계산하게 됩니다. - 1000 구간 (성공): 구간을 10배 더 잘게 쪼개자, 계산기는
x=1근처의 가파른 변화를 훨씬 촘촘하게 추적할 수 있게 되었습니다. 그 결과 훨씬 더 정확한 근사값을 얻은 것입니다.
3. Sharp 계산기 정밀 계산을 위한 실용 가이드
이러한 함정을 피하고 Sharp 계산기를 더 신뢰성 있게 사용하기 위한 단계별 가이드입니다.
1단계: 함수를 의심하라 (그래프 형태 예측)
계산 전에 함수를 살펴보세요. 분모가 0이 되는 지점, 즉 '점근선'이 있는지 확인하는 것이 첫걸음입니다.
2단계: 적분 구간을 확인하라 (위험 지역 근처인가?)
점근선이 적분 구간 안이나 아주 가까이에 있다면, 계산기의 기본 설정이 오차를 일으킬 확률이 매우 높다는 경고 신호입니다.
3단계: 수동으로 정밀도를 강제하라 (,n 활용)
위험이 감지되면, 계산식 뒤에 ,n을 추가하여 구간 개수를 직접 지정하세요. n은 구간의 수입니다.
사용법: ∫(함수, 시작값, 끝값, 구간 개수)
예시: ∫(1/((1-X)(2-X)), 0, 0.999, 1000)
*중요한 계산이라면 처음부터 1000 이상의 값을 지정하는 것이 안전합니다.

하지만 숫자가 커질수록 이렇게 BUSY 한 화면을 계속 쳐다보는 '끈기' 내지 한참 있다가 쳐다볼 '여유'가 필요합니다.
4단계 (선택): 결과를 교차 검증하라
n=1000일 때와 n=2000일 때의 결과를 비교하여, 값이 거의 변하지 않는다면 결과가 안정되었다고 믿을 수 있습니다.
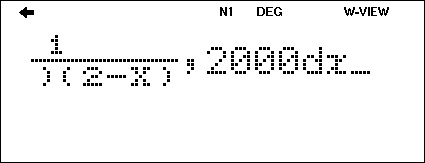

6.2170에서 6.2157 로 바뀌었으니 안정되었다고 볼 수도 있겠고, 요구하는 정밀도에 따라서 아직 멀었다고 볼 수도 있겠습니다.
4. 결론: 도구를 이해하고 지배하기
이번 사례는 공학용 계산기가 만능이 아니라 정해진 알고리즘에 따라 작동하는 도구임을 명확히 보여줍니다.
특히 Sharp 계산기는 사용자에게 '구간 개수'라는 정밀도 제어 레버를 직접 제공하며,
기본 subinterval 을 100으로 매우 작게 기본설정하여, 시간적 이득을 취하는 것을 선택하였습니다.
하지만 그 반대 급부로서 기본 오차 가능성을 크게 만들었죠.
우리는 계산기의 잠재적인 함정을 피해갈 수도 있고, 함정에 걸려버릴 수도 있습니다.
복잡한 계산일수록 계산기의 한계를 인식하고 적극적으로 사고할 필요가 있다고 하겠습니다.
아니면... 그걸 대신해줄 다른 계산기로 넘어가셔야...
댓글2
-
세상의모든계산기
다른 계산기의 경우와 비교
1. TI-nspire CAS
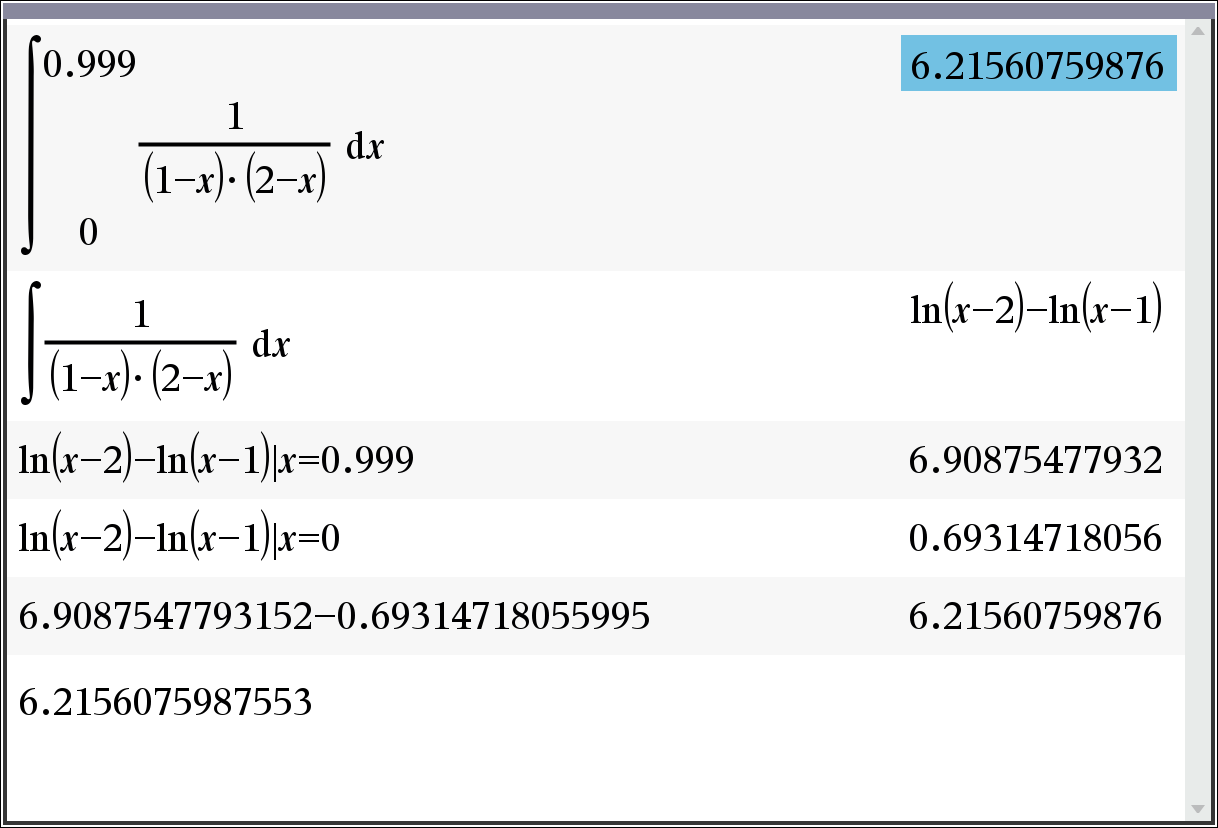
ㄴ CAS 계산기는 가능한 경우 부정적분을 먼저하고, 그 값에 구간을 대입해 최종값을 얻습니다.
ㄴ 부정적분이 불가능할 때는 수치해석적 방법을 시도합니다.
2. CASIO fx-991 ES Plus
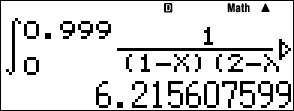
ㄴ CASIO 계산기의 경우, 적분할 함수에 따라 시간이 달라지는 것으로 알고 있는데, 정밀도를 확보할 별도의 알고리즘을 채택하고 있는 것이 아닐까 생각되네요.


세상의모든계산기 님의 최근 댓글
감사합니다. 주말 잘 보내세요. 2026 03.06 [fx-570 ES] 과학 상수를 이용한 계산에서 에러 발생 상황 https://kin.naver.com/qna/detail.naver?d1id=11&dirId=1118&docId=492235162&page=1&answerNo=1 vs 2026 03.01 과학상수를 이용한 계산 중 자릿수 한계로 인한 에러 발생 가능성 https://allcalc.org:443/board_calculators/6925#comment_57029 2026 03.01 기본 어댑터 MODEL : AD0301-1202500GB INPUT : 100~240V, 50~60Hz, 0.8A Max OUTPUT : 12.0V, 2.5A, 30.0W ㄴ 측정시 플러그 외경/내경 : 5.5mm / 2mm 2026 02.15 엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10