- TI nspire
[TI-nspire CAS] [Program] pfe, 다항식 부분분수화 프로그램 (실수단위, 복소수단위)
1. 프로그램 소개
Partial Fraction Expansion Program
for TI-Nspire CAS ver 0.1 (2015-11-17)
by allcalc.org
http://www.allcalc.org/10272
---
Define LibPub pfe(ex)=
Prgm
:
:© Set mode to Exact
:setMode(5,1)
:
:© Set mode to float6
:setMode(1,5)
:
:© Var for PFE Level
:Local level
:1→level
:
:© Determine alphabet var for inputted expression
:Local var,ds,s_denom
:string(getDenom(ex))→s_denom
:For ds,1,dim(s_denom)
: If 96<ord(mid(s_denom,ds,1))<123 Then
: expr(mid(s_denom,ds,1))→var
: Goto esc_var
: EndIf
:EndFor
:
:Disp "Use Var as ""x"" or ""s"" or ""t"" at the beginning"
:Goto end
:
:Lbl esc_var
:
:© Allocate vars for numerator,denominator,quotient,remainder
:Local ex_num,ex_denom,ex_quotient,ex_remainder
:© exact(ex)→ex
:ex_num:=getNum(ex)
:ex_denom:=getDenom(ex)
:ex_quotient:=exact(polyQuotient(ex_num,ex_denom))
:ex_remainder:=polyRemainder(ex_num,ex_denom)
:If string(exact(ex_quotient))="0" Then
: Disp "Polynomial is : ",ex
:Else
: Disp "PolyRemainder : ",ex_remainder
: Disp "Denominator : ",ex_denom
: Disp "--- --- --- ---"
:EndIf
:
:© Get Multiple Roots
:Local roots,roots_m,roots_p,roots_c,roots_r,temp_multivar
:zeros(ex_denom,var)→roots
:ex_denom|var=9999000000.→temp_multivar
:getType(temp_multivar)→temp_multivar
:If temp_multivar="NUM" Then
: polyRoots(ex_denom,var)→roots_p
:Else
: roots→roots_p
:EndIf
:
:newList(dim(roots))→roots_m
:{}→roots_c
:{}→pfe.result
:{}→pfe.resultc
:Local i
:For i,1,dim(roots)
: countIf(roots_p,roots[i])→roots_m[i]
:EndFor
:
:© Calculate coefficient for each roots
:Local j,k,temp_pd,temp_ex
:((ex_remainder)/(ex_denom))→temp_ex
:For j,1,dim(roots)
: For k,1,roots_m[j]
:(factor(((ex_num)/(ex_denom))*(var-roots[j])^(roots_m[j]),var),var,k-1)→roots_r
:
:(var-roots[j])^(roots_m[j]-k+1)→temp_pd
: augment(roots_c,{propFrac(((roots_r)/((k-1)!)))|var=roots[j]})→roots_c
: augment(pfe.result,{((roots_c[dim(roots_c)])/(temp_pd))})→pfe.result
: temp_ex-((roots_c[dim(roots_c)])/(temp_pd))→temp_ex
: EndFor
:EndFor
:
:© Check for complex roots
:If string(factor(temp_ex))≠"0" Then
: If left(string(getNum(temp_ex)),6)="1.−13" Then
: Disp "It may be Approximate Result."
: 1→level
: Goto level_approx
: EndIf
:
:© Request Level of PFE (Real or Complex)
: Request "Select PFE Level 1=Real, 2=Complex",level,0
: If string(level)≠"2" Then
: 1→level
: EndIf
:
: If level=1 Then
: augment(pfe.result,{temp_ex})→pfe.result
: Else
: Disp "PFE to Complex Number Level"
: Local exc_num,exc_denom
: exc_num:=getNum(temp_ex)
: exc_denom:=getDenom(temp_ex)
:
: Local croots,croots_c,croots_r
: cPolyRoots(exc_denom,var)→croots
: newList(dim(croots))→croots_c
: newList(dim(croots))→croots_r
:
: Local l
: For l,1,dim(croots)
: cFactor(cFactor(((exc_num)/(exc_denom)),var)*(var-croots[l]),abc987)→croots_r[l]
: cFactor(croots_r[l],abc987)|var=croots[l]→croots_c[l]
: If abs(croots_c[l])>9.−11 Then
: cFactor(augment(pfe.resultc,{((croots_c[l])/(factor(var-croots[l])))}))→pfe.resultc
: EndIf
: EndFor
:
: EndIf
:EndIf
:
:Lbl level_approx
:
:© Display result as matrix form
:If string(ex_quotient)≠"0" Then
:{ex_quotient}→pfe.resultq
: Disp factor(list▶mat(pfe.resultq))
:EndIf
:
:If dim(pfe.result)≠0 Then
: Disp factor(list▶mat(pfe.result))
:EndIf
:
:If level=2 Then
: Disp factor(list▶mat(pfe.resultc))
:EndIf
:
:If temp_multivar="EXPR" Then
: Disp "PFE once more!"
: pfe(ex_quotient)
:EndIf
:Lbl end
:EndPrgm
- 입력 예
pfe(exprs)
: 변수는 알파벳 소문자 어떤 것이라도 가능합니다. 다만, 분모의 왼쪽으로부터 처음으로 발견되어야만 합니다.
실수근에 대하여는 묻지 않고 부분분수로 강제로 나눕니다.
분모에 복소수근이 있는 경우에는, 복소수 차원으로 부분분수시킬 것인지를 프로그램이 물어볼 것입니다.
- 결과의 저장
- pfe.result (기본값, 실수범위 부분분수 결과)
- pfe.resultc (복소범위 분해 결과)
- pfe.resultq (분자/분모의 몫(quotient)이 있는 경우)
2. 사용 예제

└ 실수 수준의 부분분수화는 기본 내장함수인 expand() 를 사용하는 것이 편리합니다.

└ 계수가 소숫점 형태이거나 근사값으로 부분분수화가 진행되는 경우, expand() 에서 부분분수화가 제대로 되지 않는 때가 있습니다. 이 때는 pfe() 프로그램이 도움이 될 수 있습니다.

└ 1:Real Number 수준에서 진행한 경우. expand()와 차이가 나지 않음

└ 2:Complex Number 수준으로 진행한 경우
3. 주의사항
- 허수근에 대한 다차식이 있는 경우에는 문제가 발생함
 expand() 로 해결
expand() 로 해결 - 상수가 아닌 미지수 근에 대해서는 문제가 발생할 가능성이 큼
 expand() 로 해결
expand() 로 해결 - 프로그램 작성 초기버전이라서 기타 문제 발생 가능성이 있습니다. 제보 바랍니다.
분모나 분자에 소수점이 있는 경우 결과가 근사값 형태로 표시될 수 있습니다.
(특별한 사정이 있지 않은 이상)
분모분자에 적당한 수를 곱해 exact 계산 형태로 바꾸시는 걸 추천합니다.
└ 입력식에 소숫점이 있는 경우 (0.5)

└ 분모 분자에 10을 곱하여 입력한 경우. (10 대신 2를 곱해도 같은 결과)
※ 이것은 expand() 함수에서도 마찬가지로 적용됩니다.
댓글16
-
1
세상의모든계산기
복소범위 부분분수화한 결과가 R1+R2+R3+C1+C2 꼴이면
- pfe.result=R1+R2+R3
- pfe.resultc=C1+C2
의 결과를 얻습니다.
실수까지만 보인다고 하시니 pfe.result 를 말씀하시는 것 같네요.
그게 아니고 pfe.resultc 를 그냥 호출하신 경우라면, 계산기의 고유한 특징으로 인하여 변수에 저장된 값에 상관없이 결과를 화면에 표시할 때는 무조건 분모를 유리화합니다.

따라서 유리화하지 않고 그대로 다시 보기 위해서는 factor(pfe.resultc) 로 불러내야 합니다.
[추가] 변수 s를 s_로 변경하는 방법도 가능하네요.
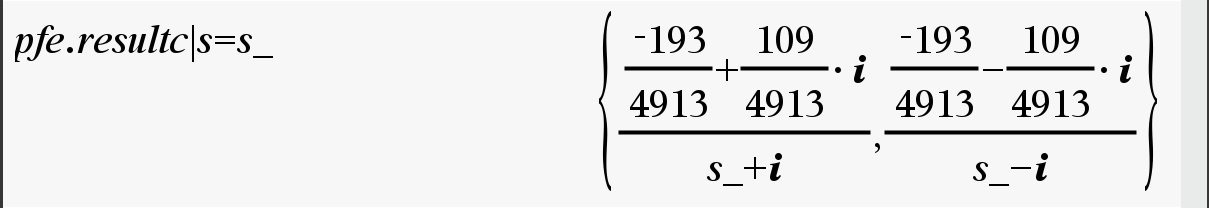
- 2
-
2
세상의모든계산기
factor()를 사용하지 않고, 변수를 s 대신 s_ 로 대치
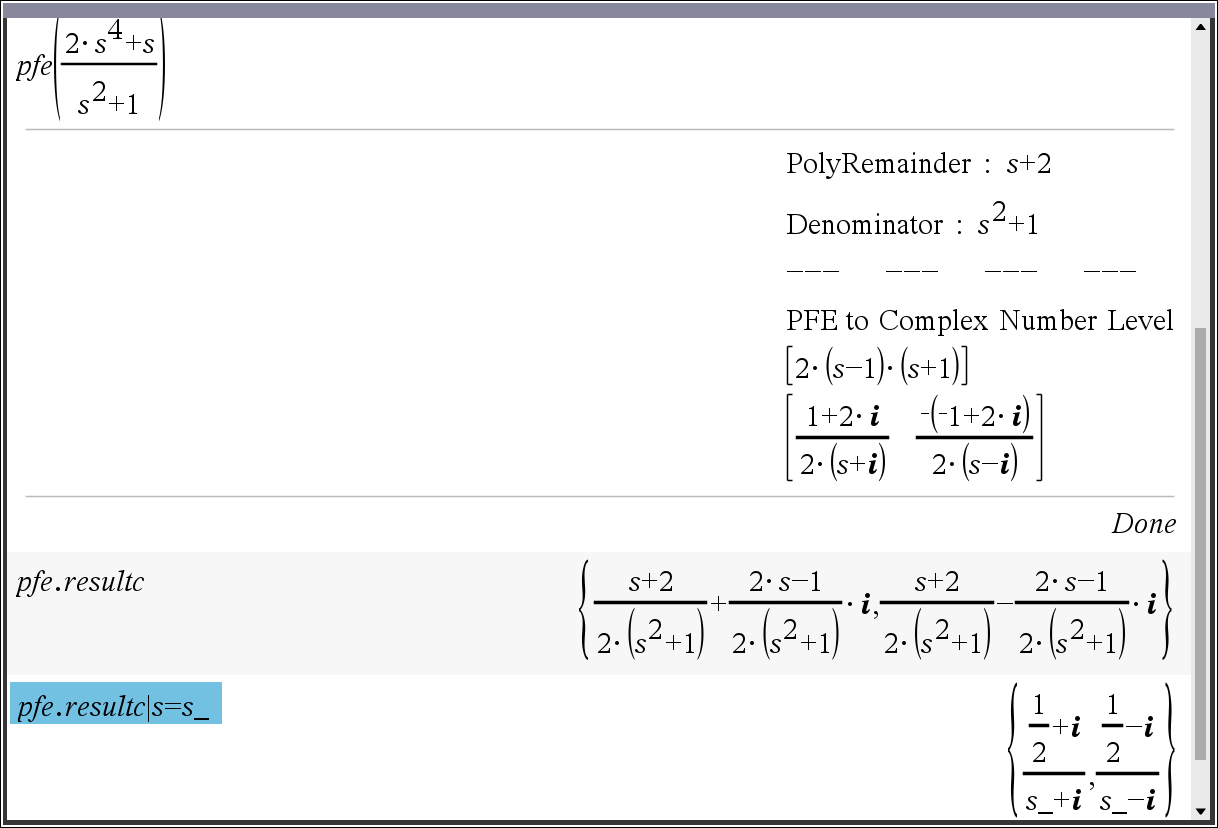
프로그램을 수정해서 변수를 모두 s_로 바꾸는게 나을런지?
복소수 결과 pfe.resultc 만 s_ 로 바꾸는게 나을런지?
-
세상의모든계산기
간혹 버그가 발생하네요.

저렇게 2.1E-12 와 같이 작은 숫자가 곱해진 부분은 버그일 가능성을 의심해보시는게 좋겠습니다.
* 프로그램을 고칠 가능성은 현재로선 낮습니다. -_-'
- 1
-
ytg0602
프로그램을 쓰던 중에 오류가 생겨서 댓글 달아봅니다. 매트랩 홈페이지에서 부분 분수 전개에 대한 예제에 대한 식으로 한번 프로그램을 써봤는데요.
각각 해당 식들을 입력하고 복소수 레벨에서 실행시키면 에러 메시지가 A conditional statement did not resolve to TRUE or FALSE라는 메시지가 뜹니다. level 누를 때 2로 눌렀던 걸로 기억합니다. 보니까 조건식에서 에러가 나는 것 같은데 혹시 버그인지 제가 사용법을 몰라서 못 쓰는 건지 궁금합니다.
해당 매트랩 홈페이지 주소는 https://kr.mathworks.com/help/matlab/ref/residue.html입니다.
그리고 해당 식들은 (2*s^3+s^2)/(s^3+s^2+1)과 (2*s^4+s)/(s^2+1)입니다. -
1
세상의모든계산기
첫번째 예제는 ERROR가 나는 상황이고,
두번째 예제는 문제가 없는 듯 합니다.
버그가 맞구요.
뭔가 잘못된 건 확실한데...디버깅하는 것이
저에게는 0에서 다시 시작하는 것과 같기 때문에 손이 가질 않네요. - 2
- 1
-
세상의모든계산기2023.04.11 - 18:35 #38678오픈 AI에 코드를 보여주니
LibPub pfe()는 Casio 계산기에서 지원하는 프로그래밍 언어로 작성된 프로그램입니다. 주어진 유리 함수의 PFD(partial fraction decomposition)를 찾기 위해 설계된 사용자 정의 함수로 미적분학 및 대수학에서 유용한 기법입니다. 프로그램은 먼저 계산기를 Exact 모드와 float6 모드로 설정합니다. 그런 다음 사용자에게 분수 형식의 유리수 함수를 입력하라는 메시지가 표시됩니다. 그런 다음 프로그램은 "x", "s" 또는 "t" 식에 사용된 변수를 식별합니다. 사용된 변수가 이 세 가지 중 하나가 아니면 프로그램은 오류 메시지를 표시합니다. 다음으로, 프로그램은 분모에 의한 분자의 다항식 나눗셈의 몫과 나머지를 찾습니다. 몫이 0이면 프로그램은 원래 다항식을 표시합니다. 그렇지 않으면 나머지와 분모를 표시합니다. 그런 다음 프로그램은 분모의 여러 근을 찾고 각 근에 대한 계수를 계산합니다. 복소수가 있는 경우 PFD 수준(실수 또는 복소수)을 선택하라는 메시지가 표시됩니다. 실제인 경우 프로그램은 결과를 행렬로 표시합니다. 복소수인 경우 프로그램은 복소수 근을 찾아 해당 계수를 계산하고 결과를 행렬로 표시합니다. 전반적으로 LibPub pfe()는 많은 수학적 문제를 해결하는 데 필수적인 유리 함수의 부분 분수 분해를 찾는 강력한 도구입니다. -
1
세상의모든계산기2023.04.11 - 18:36 #38681개선할 점은 없냐 물어보니...
귀하의 프로그램은 잘 작성되고 포괄적인 것 같습니다. 그러나 개선을 위한 몇 가지 제안을 제공할 수 있습니다.
오류 처리 추가: 프로그램은 사용자가 유효한 입력을 입력했다고 가정합니다. 사용자가 잘못된 입력을 입력하는 경우 프로그램 충돌을 방지하기 위해 오류 처리를 추가하는 것이 도움이 될 것입니다.
가독성 향상: 주석을 추가하고 긴 코드 줄을 여러 줄로 나누어 코드의 가독성을 높일 수 있습니다.
설명이 포함된 변수 이름 추가: 일부 변수 이름은 짧고 설명이 많지 않습니다. 더 설명적인 변수 이름을 사용하면 코드를 더 쉽게 이해할 수 있습니다.
사용자가 변수 이름을 입력하도록 허용: 사용자에게 특정 변수 이름을 사용하도록 요청하는 대신 사용하려는 변수 이름을 입력하도록 허용할 수 있습니다.
더 많은 옵션 추가: 프로그램은 현재 다항식의 부분 분수 확장 계산만 지원합니다. 함수의 라플라스 변환 계산과 같은 더 많은 옵션을 추가하는 것을 고려할 수 있습니다. - 1
-
1
세상의모든계산기
Exact float6 Disp "Enter rational function in the form of a/b(x)" Prompt a,b,x If x="x" or x="s" or x="t" Then q:=a/b // 몫 계산 r:=a-q*b // 나머지 계산 If q=0 Then Disp "The original polynomial is:" Disp r Else Disp "The quotient is:" Disp q Disp "The remainder is:" Disp r EndIf roots:=poly_roots(b,x) coeffs:=List(0,dim(roots)) For i,root In roots Do If Im(root)=0 Then // 근이 실수인 경우 coeff:=limit(a/b/(x-root),x,root) Else // 근이 복소수인 경우 Disp "Select PFD level for complex roots of", root Menu "PFD Level", ["Real", "Complex"] If Ans=1 Then // PFD level: Real coeff:=limit(a/b/(x-root),x,root) Else // PFD level: Complex coeff_real:=limit(a/b/(x-Re(root)),x,Re(root)) coeff_imag:=limit(a/b/(x-Im(root)),x,Im(root)) coeff:=Matrix([[coeff_real,coeff_imag],[-coeff_imag,coeff_real]]) EndIf EndIf coeffs[i]:=coeff EndFor If dim(roots)=0 Then Disp "No roots found." Else Disp "Coefficients:" Disp coeffs EndIf Else Disp "Error: Invalid variable used" Stop EndIf설명만 입력하고 ti nspire 용으로 만들어 달랬더니 위와 같이 만들어줬습니다.
대충 ti basic 하고 비슷은 한데, 못쓰는 명령어도 짬뽕되어 있고 그렇네요.


세상의모든계산기 님의 최근 댓글
3×3 이상인 행렬의 행렬식 determinant https://allcalc.org/50536 2025 12.30 답에 이상한 숫자 14.2857142857가 들어간 것은 조건식에 소숫점(.) 이 들어가 있기 때문에 발생한 현상이구요. 100÷7 = 14.285714285714285714285714285714 소숫점 없이 분수로 식이 주어졌을 때와 결과적으로는 동일합니다. 2025 12.30 그럼 해가 무한히 많은지 아닌지 어떻게 아느냐? 고등학교 수학 교과과정에 나오는 행렬의 판별식(d, determinant)을 이용하면 알 수 있습니다. ㄴ 고교과정에서는 2x2 행렬만 다루던가요? 연립방정식의 계수들로 행렬을 만들고 그 행렬식(determinant)을 계산하여야 합니다. 행렬식이 d≠0 이면 유일한 해가 존재하고, d=0 이면 해가 없거나 무수히 많습니다. * 정상적인 경우 (`2y + 8z = 115`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 8 | 행렬식 값 = 1(0 - (-7)) - 1(8 - 0) = 7 - 8 = -1 (0이 아니므로 유일한 해 존재) * 문제가 된 경우 (`2y + 7z = 100`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 7 | 행렬식 값 = 1(0 - (-7)) - 1(7 - 0) = 7 - 7 = 0 (0이므로 유일한 해가 존재하지 않음) 2025 12.30 좀 더 수학적으로 말씀드리면 (AI Gemini 참고) 수학적 핵심 원리: 선형 독립성(Linear Independence) 3원 1차 연립방정식에서 미지수 x, y, z에 대한 단 하나의 해(a unique solution)가 존재하기 위한 필수 조건은 주어진 세 개의 방정식이 서로 선형 독립(linearly independent) 관계에 있어야 한다는 것입니다. * 선형 독립 (Linearly Independent): 어떤 방정식도 다른 방정식들의 조합(상수배를 더하거나 빼는 등)으로 만들어질 수 없는 상태입니다. 기하학적으로 이는 3개의 평면(각 방정식은 3D 공간의 평면을 나타냄)이 단 한 개의 점(해)에서 만나는 것을 의미합니다. * 선형 종속 (Linearly Dependent): 하나 이상의 방정식이 다른 방정식들의 조합으로 표현될 수 있는 상태입니다. 이 경우, 새로운 정보를 제공하지 못하는 '잉여' 방정식이 존재하는 것입니다. 기하학적으로 이는 3개의 평면이 하나의 선에서 만나거나(무수히 많은 해), 완전히 겹치거나, 혹은 평행하여 만나지 않는(해가 없음) 상태를 의미합니다. 질문자님의 사례는 '선형 종속'이 되어 무수히 많은 해가 발생하는 경우입니다. 2025 12.30 질문하신 연립 방정식은 미지수가 3개이고 모두 1차인 3원 1차 연립방정식입니다. 이상적으로 문제가 없다면 {x,y,z} 에 대한 좌표가 하나 나오게 됩니다. 원하는 답 {52.5, -2.5, 15} 그런데 두개 조건(식)을 그대로 두고 나머지 하나를 변형하다 보니 원하는 답이 나오지 않는 상황이 발생하였다고 질문하신 상황입니다. 3개의 조건식이 주어진 3원 1차 연립방정식은 조건을 변형해서 하나의 변수를 제거할 수 있습니다. 그러면 2개의 조건식으로 주어지는 2원 1차 연립방정식으로 변형할 수 있습니다. (알아보기 더 쉬워서 변형하는 겁니다) 변경하지 않은 조건의 식(con1) 을 이용해 하나의 y & z 1차 방정식을 유도할 수 있는데요. 나머지 방정식이 con1에서 유도된 방정식과 동일해지면 하나의 답이 구해지지 않는 것입니다. 계산기(ti-nspire)는 {x,y,z} 의 답이 하나가 아니고 무수히 많음을 c1 을 이용해서 표현해 준 것입니다. linear_independence_cond12.tns 2025 12.30