- TI nspire
[TI-nspire] FormulaPro - 전기 공학 문제 풀이용 툴
원본 출처 : https://tiplanet.org/forum/archives_voir.php?id=6034
github : https://github.com/adriweb/EEPro-for-Nspire
설명서 pdf (영문) : https://education.ti.com/-/media/C024C65A3D5247D083021DCDA3E73369
ㄴ 프로그램이 간략하게 소개되었을 뿐 큰 도움이 되진 않으니,
ㄴ 자세한 설명이 필요한 경우 TI-89/92 용 오리지널 프로그램인 EEPro 설명서(pdf)를 읽어보시는게 좋습니다.
ㄴ https://education.ti.com/en-ph/guidebook/details/en/95B2DF8D3F5A47DE88257AE45C2EA867/89eepro
소개글 한국어 AI 번역 (ChatGPT)
FormulaPro란?
FormulaPro는 TI-Nspire 계산기를 위한 프로그램으로, 전기 공학 문제를 해결하는 EEPro(TI-89/92용)의 일부를 TI-Nspire용으로 이식한 프로젝트입니다. FormulaPro는 무료이자 오픈 소스(LGPL 라이선스)이며, Lua 스크립트로 작성된 TI-Nspire 문서(OS 3.x 이상 지원)입니다.
주요 기능:
1. 모든 TI-Nspire 모델 및 소프트웨어에서 작동하며 창 크기 자동 조정 지원.
2. 마우스와 키보드를 모두 지원.
3. 사용자 정의 방정식 세트를 생성 가능(변수 및 단위 연결).
4. 방정식 자동 해결(사용자가 값을 입력하면 자동으로 풀이).
5. 다양한 단위/하위 단위 선택 가능(예: Hz/kHz/MHz, °C/°F/K 등).
6. 사용된 방정식을 시각적으로 표시("Pretty Print" 모드 지원).
사용 방법:
1. TI-Nspire OS 3.0 이상 필요(3.2 이상 권장).
2. 기본 제공되는 데이터베이스(EEPro 일부) 사용 또는 [온라인 데이터베이스 생성기](https://tiplanet.org/scripts/FormulaProGenerator/)를 이용해 데이터베이스 생성 가능.
3. 생성한 `.tns` 파일을 계산기에 전송 후 열기.
4. 카테고리 및 하위 카테고리를 선택 후 데이터를 입력하면 자동 풀이.
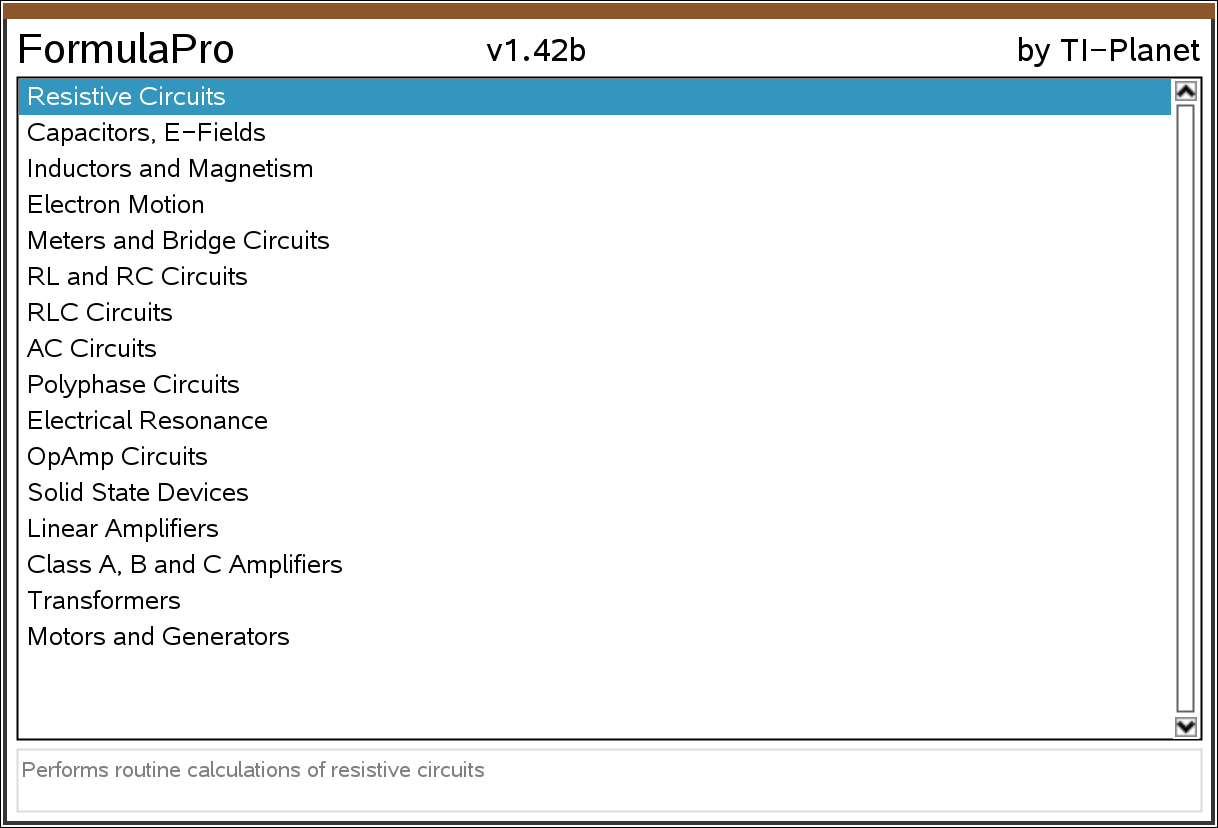
메뉴
Resistive Cirtuits : Performs routine calculations of resistive circuits
Capacitors, E-Fields : Compute electric fields properties and capacitance of various types of structures
Inductors and Magnetism : Calculate electrical and magnetic properties of physical elements
Electron Motion : Investigate the trajectories of electrons under the influence of electric and magnetic fields
Meter and Bridge Circuits : This Category covers a variety of topics on meters, commonly used bridge and attenuator circuits
RL and RC Circuits : Compute the natural and transient properties of simple RL and RC circuits
RLC Circuits : Compute the impedence, admittance, natural response and transient behavior of RLC circuits
AC Circuits : Calculate properties of AC circuits
Polyphase Circuits
Electrical Resonance
OpAmp Circuits
Solid State Devices
Linear Amplifiers
Class A, B, and C Amplifiers
Transformers
Motors and Generators
향후 계획 (FormulaPro 2.0):
- TI-Nspire 내에서 데이터베이스 편집 가능.
- 더 강력한 방정식 풀이 알고리즘.
- 스마트 검색(단위만 입력하면 자동으로 관련 방정식 찾기).
- 카테고리별 이미지 추가(회로도, 설명 등).
- Vernier 센서를 통해 데이터 직접 입력.
- 다국어 지원.
- 결과 그래프화.
FormulaPro는 EEPro의 모든 기능을 포함하고, 이를 뛰어넘는 기능을 목표로 합니다.
추가 정보 및 버그 보고:
- FormulaPro 팀: [tiplanet.org](http://tiplanet.org), [inspired-lua.org](http://www.inspired-lua.org)


세상의모든계산기 님의 최근 댓글
3×3 이상인 행렬의 행렬식 determinant https://allcalc.org/50536 2025 12.30 답에 이상한 숫자 14.2857142857가 들어간 것은 조건식에 소숫점(.) 이 들어가 있기 때문에 발생한 현상이구요. 100÷7 = 14.285714285714285714285714285714 소숫점 없이 분수로 식이 주어졌을 때와 결과적으로는 동일합니다. 2025 12.30 그럼 해가 무한히 많은지 아닌지 어떻게 아느냐? 고등학교 수학 교과과정에 나오는 행렬의 판별식(d, determinant)을 이용하면 알 수 있습니다. ㄴ 고교과정에서는 2x2 행렬만 다루던가요? 연립방정식의 계수들로 행렬을 만들고 그 행렬식(determinant)을 계산하여야 합니다. 행렬식이 d≠0 이면 유일한 해가 존재하고, d=0 이면 해가 없거나 무수히 많습니다. * 정상적인 경우 (`2y + 8z = 115`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 8 | 행렬식 값 = 1(0 - (-7)) - 1(8 - 0) = 7 - 8 = -1 (0이 아니므로 유일한 해 존재) * 문제가 된 경우 (`2y + 7z = 100`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 7 | 행렬식 값 = 1(0 - (-7)) - 1(7 - 0) = 7 - 7 = 0 (0이므로 유일한 해가 존재하지 않음) 2025 12.30 좀 더 수학적으로 말씀드리면 (AI Gemini 참고) 수학적 핵심 원리: 선형 독립성(Linear Independence) 3원 1차 연립방정식에서 미지수 x, y, z에 대한 단 하나의 해(a unique solution)가 존재하기 위한 필수 조건은 주어진 세 개의 방정식이 서로 선형 독립(linearly independent) 관계에 있어야 한다는 것입니다. * 선형 독립 (Linearly Independent): 어떤 방정식도 다른 방정식들의 조합(상수배를 더하거나 빼는 등)으로 만들어질 수 없는 상태입니다. 기하학적으로 이는 3개의 평면(각 방정식은 3D 공간의 평면을 나타냄)이 단 한 개의 점(해)에서 만나는 것을 의미합니다. * 선형 종속 (Linearly Dependent): 하나 이상의 방정식이 다른 방정식들의 조합으로 표현될 수 있는 상태입니다. 이 경우, 새로운 정보를 제공하지 못하는 '잉여' 방정식이 존재하는 것입니다. 기하학적으로 이는 3개의 평면이 하나의 선에서 만나거나(무수히 많은 해), 완전히 겹치거나, 혹은 평행하여 만나지 않는(해가 없음) 상태를 의미합니다. 질문자님의 사례는 '선형 종속'이 되어 무수히 많은 해가 발생하는 경우입니다. 2025 12.30 질문하신 연립 방정식은 미지수가 3개이고 모두 1차인 3원 1차 연립방정식입니다. 이상적으로 문제가 없다면 {x,y,z} 에 대한 좌표가 하나 나오게 됩니다. 원하는 답 {52.5, -2.5, 15} 그런데 두개 조건(식)을 그대로 두고 나머지 하나를 변형하다 보니 원하는 답이 나오지 않는 상황이 발생하였다고 질문하신 상황입니다. 3개의 조건식이 주어진 3원 1차 연립방정식은 조건을 변형해서 하나의 변수를 제거할 수 있습니다. 그러면 2개의 조건식으로 주어지는 2원 1차 연립방정식으로 변형할 수 있습니다. (알아보기 더 쉬워서 변형하는 겁니다) 변경하지 않은 조건의 식(con1) 을 이용해 하나의 y & z 1차 방정식을 유도할 수 있는데요. 나머지 방정식이 con1에서 유도된 방정식과 동일해지면 하나의 답이 구해지지 않는 것입니다. 계산기(ti-nspire)는 {x,y,z} 의 답이 하나가 아니고 무수히 많음을 c1 을 이용해서 표현해 준 것입니다. linear_independence_cond12.tns 2025 12.30