- TI nspire
[TI-nspire] 행렬 LU 분해 = LU Decomposition = LU fatorization
-
- 2025.04.20 - 15:35 2015.11.02 - 15:55 6719 7
1. LU 분해란?
행렬 A 를 Lower 행렬과 Upper 행렬의 곱으로 분해하는 것을 의미합니다.
A = L×U 를 만족하는 행렬 L과 행렬 U를 찾는 과정이라고 할 수 있습니다.
2. TI-nspire 에서의 LU 명령어
분명 책에서는 A를 그냥 L*U 로 분해하라고 했는데...
nspire 에서는 P*A = L*U 꼴로 지맘대로 변형하여 분해하기 때문에 답안지와 다른 풀이를 보여줄 수도 있습니다.
원하는 L × U = A
nspire 에서 바뀌어버린 1행과 2행
LU Matrix,lMatrix,uMatrix,pMatrix[,Tol]
ㄴ permutation matrix 를 보면 1행과 2행이 바뀐 상황
3. 
팁 : 행이 섞이지 않게 만드는 방법
행렬을 LU 꼴로 분해하기 위해 반드시 P(Permutation)를 곱해서 행의 순서를 바꾸어야만 하는 경우도 있습니다만, 바꾸지 않고도 L*U 분해를 할 수 있음에도 TI 계산기에서 P를 이용해 행의 순서를 바꾸는 경우가 있습니다.
P를 활용한 LU분해도 틀린 답은 아니지만... 우리가 원하는 형태의 답은 아닐 수 있기 때문에 (필수적이지 않은!) Permutation 을 피해서, L*U 분해하는 방법을 찾아보겠습니다.
먼저 "TI의 LU명령에서 행이 바뀌는 원인"을 알아야 합니다. TI-nspire 에서는 LU 명령시에 계수의 절대값을 비교하여 큰 순서로 재배치합니다. (반드시 Permutation 이 일어나야 하는 경우도 결합하여 실행됩니다)
* 1행 기준은 아니고, 2행 기준으로 하기도 하고... 그렇네요.
따라서, 행이 바뀌지 않기를 바란다면 특정 행의 요소 전부에 어떤 값을 곱하여 1열의 계수 절대값을 (원하는 순서대로) 내림차순으로 만들어야 합니다.
위의 예에서는 1행 1열의 계수와 2행 1열의 계수가 각각 2와 4로서 2행*1열의 절대값이 더 큰 상태입니다. 따라서 1행 전체를 3이상의 수를 곱하여 주면 크기순으로 정리가 됩니다. 그 다음에 LU 명령으로 분해하고 ⇒ 분해된 L'과 U'를 다시 적당히 가공하면 우리가 원하는 답이 도출됩니다.
<과정 1>
A행렬의 1행만을 10배로 만드는 행렬을 M 행렬이라고 하면, M × A = L' × U' 꼴로 분해
ㄴ 일단 순서가 바뀌지 않게 하는 것은 성공함.
<과정 2>
<과정1>은 M × A = L' × U' 꼴로 분해되었으니, 
이를 A = L×U 로 재가공
A = (M-1 × L' × M) × (M-1 × U')
L = M-1 × L' × M
U = M-1 × U'
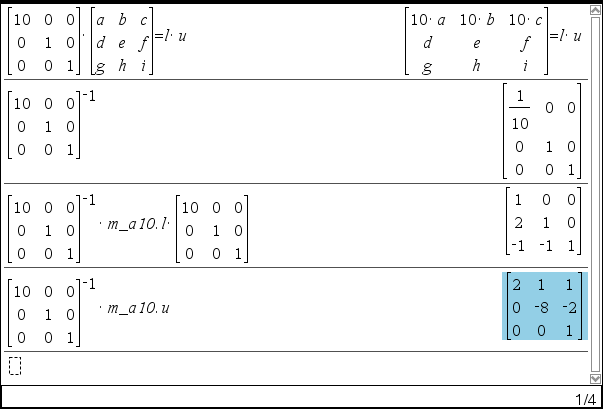
※ A= M-1 × L' × U' 의 간단한 꼴이 아닌 A= (M-1 × L' × M) × (M-1 × U') 와 같은 복잡한 식으로 만든 이유는 L의 대각성분을 1로 만들기 위함입니다.
그런데, 계수의 비교는 1열에서 끝나는 것이 아니고, 1열을 꼴로 만든 후, 2열의 계수를 다시 비교하게 됩니다. 따라서 (2행과 3행의) 2열끼리 계수도 내림차순이 되도록 m배 행렬을 잘 만들 필요가 있습니다.
위의 예제에서는 다행히도 문제가 발생하지는 않았습니다.
이 방법은 중간에 Pivot 이 0 이 되어서 반드시 Permutation 을 하여야 하는 경우까지 해결해 주진 않습니다.
-
25
댓글7
-
세상의모든계산기
아래 링크의 행렬을 분해하여 보겠습니다.
http://blog.naver.com/mykepzzang/220147195141
1행, 2행, 3행의 1열 계수가 완전 역순으로 배열되어 있습니다.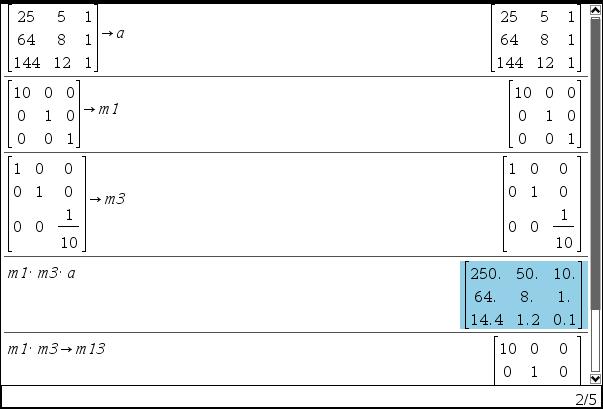
1행과 3행을 각각 m1배, m3배 하여줍니다.
분해된 U와 M을 가공하여 원래의 Lower, Upper Matrix를 뽑아냅니다.
-
세상의모든계산기
1. 크라우트법
A=L×U 로 분해하는 또 다른 방법은 크라우트법(=Crout Method)이라고 불리는데, 위의 분해와 반대로 U의 대각행렬의 값에 1을 넣고, L의 대각행렬에 1이 아닌 값을 넣는 것입니다.
이 방법은 nspire 내부 기능으로 구현되어 있지 않으므로, 프로그램을 새로 만들어서 실행하거나, nspire의 LU 기능으로 구해진 값을 가공하여 얻어야 합니다.
2. 가공 방법
Nspire에 의한 분해를 A=L×U라고 하고, Crout Method 에 의한 분해를 A=L'×U' 라고 하면
- LU 명령으로 L과 U 를 구하고, U에서 대각행렬 D 를 찾아냄
주의 : A의 대각행렬이 아니고 U의 대각행렬임 - L' = L×D
- U' = D-1×U
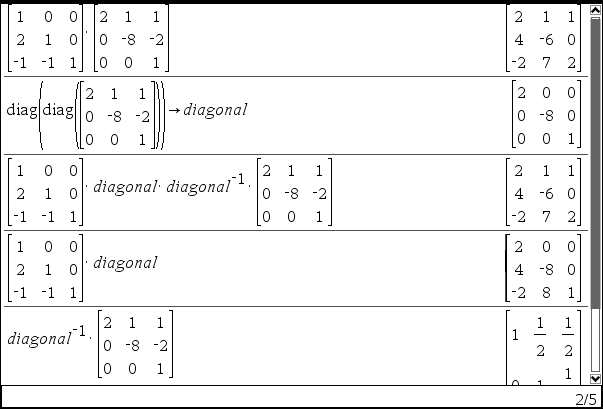
ㄴ diag(diag(U)) 함수를 두번 돌린 이유는.... 해보시면 압니다. - LU 명령으로 L과 U 를 구하고, U에서 대각행렬 D 를 찾아냄
-
1
세상의모든계산기
예시
https://kin.naver.com/qna/detail.naver?d1id=11&dirId=111301&docId=484354094&qb=6rOE7IKw6riw&enc=utf8&answerNo=1 -
세상의모든계산기
LU 프로그램 (TI nspire의 LU 기능 사용하지 않음)
LU 분해는 주어진 정방행렬 A를 하삼각행렬 L(Lower triangular matrix)과 상삼각행렬 U(Upper triangular matrix)의 곱으로 분해하는 과정입니다.
즉, A = LU를 만족하는 L과 U를 찾는 것입니다.
알고리즘의 주요 단계는 다음과 같습니다:
1. 초기화:
- n x n 크기의 단위행렬 L을 생성합니다.
- n x n 크기의 0행렬 U를 생성합니다.2. 행렬 분해:
- i = 1부터 n까지 반복:
- j = 1부터 n까지 반복:
- U의 원소(i ≤ j인 경우)와 L의 원소(i > j인 경우)를 계산합니다.3. U 행렬 계산 (i ≤ j):
u[i,j] = a[i,j] - Σ(k=1 to i-1) l[i,k] * u[k,j]4. L 행렬 계산 (i > j):
l[i,j] = (a[i,j] - Σ(k=1 to j-1) l[i,k] * u[k,j]) / u[j,j]이 알고리즘을 코드에 적용하면 다음과 같습니다:
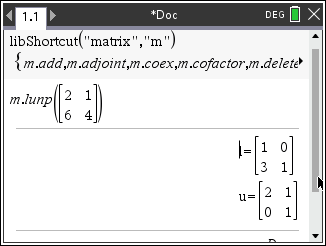
Define LibPub lunp(matrix)= Prgm :Local n,i,j,k,summ : :n:=dim(matrix)[1] :l:=identity(n) :u:=newMat(n,n) : :For i,1,n : For j,1,n : summ:=0 : For k,1,i-1 : summ:=summ+l[i,k]*u[k,j] : EndFor : If i≤j Then : u[i,j]:=matrix[i,j]-summ : Else : l[i,j]:=((matrix[i,j]-summ)/(u[j,j])) : EndIf : EndFor :EndFor : : :Disp "l=",l :Disp "u=",u :EndPrgm
이 과정을 통해:
1. U 행렬의 대각선 및 상삼각 부분이 채워집니다.
2. L 행렬의 하삼각 부분이 채워집니다 (대각선은 이미 1로 초기화되어 있음).각 단계에서 이전에 계산된 L과 U의 원소들을 사용하여 새로운 원소를 계산합니다. 이 과정이 모든 원소에 대해 반복되면, 최종적으로 A = LU를 만족하는 L과 U 행렬이 생성됩니다.
이 알고리즘의 핵심은 가우스 소거법과 유사하지만, 원래 행렬의 원소들을 L과 U에 적절히 분배하는 것입니다.
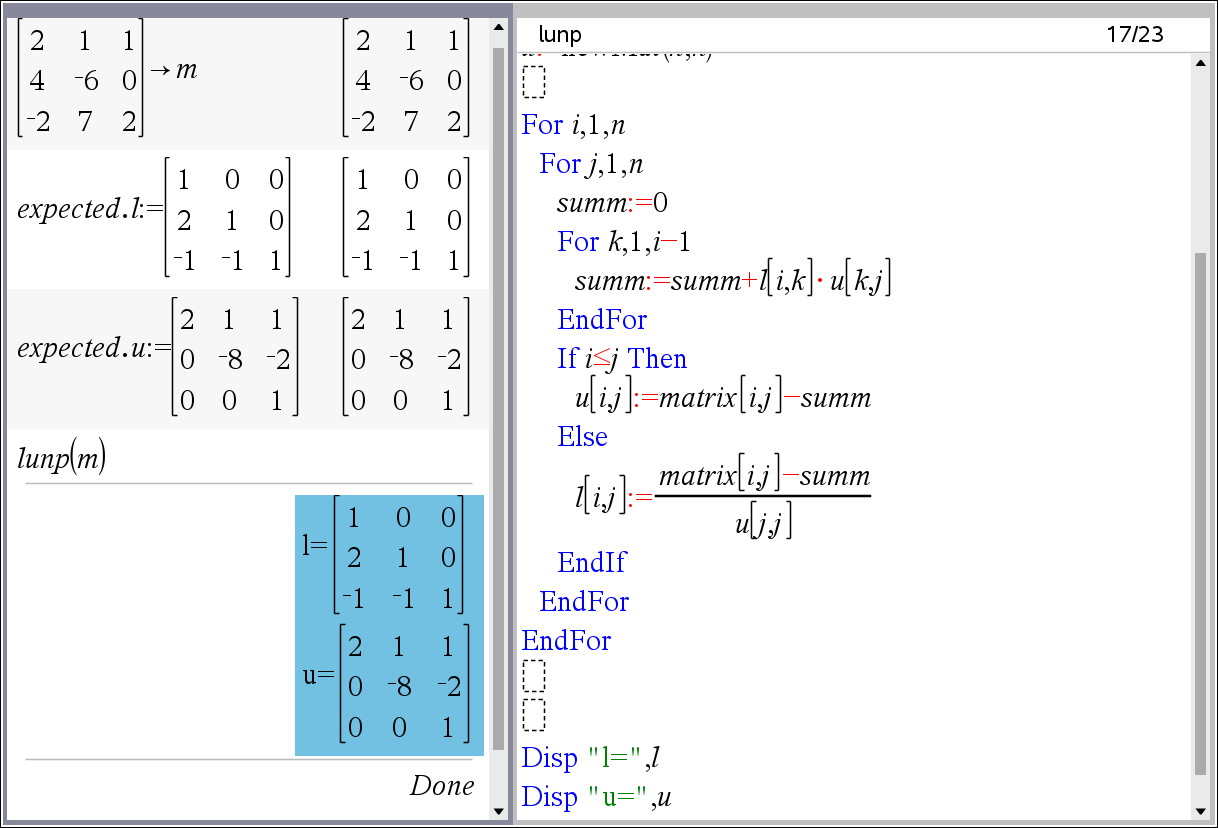
별도의 라이브러리로 만드는 것보다는
matrix 확장 라이브러리에 추가해 두는게 좋겠네요.
https://allcalc.org/1843
-
세상의모든계산기
LU 분해는 조건에 따라 답이 여러 개가 나올 수 있습니다.
🎯 핵심 개념 요약
LU 분해란 어떤 행렬 AA를 두 개의 행렬 L (Lower triangular)과 U (Upper triangular)로 나누는 것인데요, 다음과 같은 형태예요:
A=L*U
하지만 이 분해가 "유일한 해를 갖는가?" 에 대해서는 다음과 같은 조건들이 영향을 줍니다.
💡 LU 분해의 유일성 여부는?
-
Pivoting(피벗팅) 없이 LU 분해할 때
-
모든 주대각선 원소들이 0이 아니고 (즉, 행 교환 없이도 가능한 경우)
-
L의 대각 원소를 모두 1로 제한하면
→ LU 분해는 유일합니다.
-
-
Pivoting을 허용하거나, L에 1이 아닌 대각선 값을 허용하면
→ LU 분해는 여러 개가 가능합니다.
즉, 어떤 조건을 주느냐에 따라 하나로 정해지거나, 여러 개가 될 수 있어요.
예를 들어
아래와 같은 A에 대해:
\begin{bmatrix} 2 & 4 & 6 \\ 1 & 3 & 5 \\ 0 & 2 & 4 \\ \end{bmatrix}
이걸 LU로 분해할 때:
-
Pivot 없이 L의 대각을 1로 고정하면, LU는 유일함.
-
다른 방식으로 분해하거나, Partial Pivoting을 사용하면 P, L, U의 조합은 여러 가지가 나올 수 있어요.
결론
LU 분해는 조건을 명확히 지정하지 않으면, 일반적으로 유일하지 않을 수 있습니다.
-
-
1
세상의모든계산기
피벗 없이, L의 대각선을 모두 1로 고정한 LU 분해 예제를 같이 해볼게요.
🎯 예제 행렬
$$ A = \begin{bmatrix} 2 & 4 & 6 \\ 1 & 3 & 5 \\ 0 & 2 & 4 \\ \end{bmatrix} $$
이걸 다음과 같이 분해할 거예요:
A=LU
-
L: 단위 하삼각행렬 (대각선이 1)
-
U: 상삼각행렬
🧩 Step 1: 초기 형태 설정
$$ L = \begin{bmatrix} 1 & 0 & 0 \\ l_{21} & 1 & 0 \\ l_{31} & l_{32} & 1 \\ \end{bmatrix}, \quad U = \begin{bmatrix} u_{11} & u_{12} & u_{13} \\ 0 & u_{22} & u_{23} \\ 0 & 0 & u_{33} \\ \end{bmatrix} $$
🧮 Step 2: 곱셈해서 좌변과 우변 비교
$$ LU = \begin{bmatrix} 1 & 0 & 0 \\ l_{21} & 1 & 0 \\ l_{31} & l_{32} & 1 \\ \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} & u_{13} \\ 0 & u_{22} & u_{23} \\ 0 & 0 & u_{33} \\ \end{bmatrix} = \begin{bmatrix} u_{11} & u_{12} & u_{13} \\ l_{21}u_{11} & l_{21}u_{12} + u_{22} & l_{21}u_{13} + u_{23} \\ l_{31}u_{11} & l_{31}u_{12} + l_{32}u_{22} & l_{31}u_{13} + l_{32}u_{23} + u_{33} \\ \end{bmatrix} $$
이걸 원래 A와 비교:
$$ \begin{bmatrix} 2 & 4 & 6 \\ 1 & 3 & 5 \\ 0 & 2 & 4 \\ \end{bmatrix} $$
항목별 비교해봅시다.
🔍 Step 3: 항목별 대입
-
첫 행:
$$ u_{11} = 2,\quad u_{12} = 4,\quad u_{13} = 6 $$ -
두 번째 행:
$$ l_{21} \cdot 2 = 1 \Rightarrow l_{21} = \frac{1}{2} $$
$$ l_{21} \cdot 4 + u_{22} = 3 \Rightarrow 2 + u_{22} = 3 \Rightarrow u_{22} = 1 $$
$$ l_{21} \cdot 6 + u_{23} = 5 \Rightarrow 3 + u_{23} = 5 \Rightarrow u_{23} = 2 $$ -
세 번째 행:
$$ l_{31} \cdot 2 = 0 \Rightarrow l_{31} = 0 $$
$$ l_{31} \cdot 4 + l_{32} \cdot 1 = 2 \Rightarrow 0 + l_{32} = 2 \Rightarrow l_{32} = 2 $$
$$ l_{31} \cdot 6 + l_{32} \cdot 2 + u_{33} = 4 \Rightarrow 4 + u_{33} = 4 \Rightarrow u_{33} = 0 $$
✅ 결과
$$ L = \begin{bmatrix} 1 & 0 & 0 \\ \frac{1}{2} & 1 & 0 \\ 0 & 2 & 1 \\ \end{bmatrix},\quad U = \begin{bmatrix} 2 & 4 & 6 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \\ \end{bmatrix} $$
⚠️ 참고사항
-
UU의 마지막 대각 원소가 0 → 이건 A가 가역행렬이 아님을 의미해요 (즉, det(A) = 0).
-
그래도 LU 분해는 가능함! 단, 유일성은 위와 같이 조건을 명확히 해야 해요.
-
-
2
세상의모든계산기
LU 기능 이용 :
ㄴ 퍼뮤테이션 있음.
퍼뮤테이션 없애려면 계수행렬(m) 곱해야 함.
프로그램(라이브러리) 이용
ㄴ 라이브러리 : https://allcalc.org/1843
nspire 에서 기본 기능(함수)인 LU 만을 이용하는 경우,
하삼각행렬의 대각행렬이 1이 아닌 L*U 로 분해할 방법은 없는 듯 합니다.
세상의모든계산기 님의 최근 댓글
2번 사진 3개 사진 공통적으로 구석(corner) 에 증상이 있다는 특징이 있네요. 2025 10.29 500! 의 십진수 근사값 확인 500! = 1.22013682599111006870123878542304692625357434280319284219241358838 × 10^(1134) (참값, 울프람 알파) 2025 10.29 관련 라이브러리 https://allcalc.org/56263 sgn(x) 내장된 부호 함수(signum function)와 달리, 이 함수의 sgn(0)은 0을 반환합니다. 2025 10.29 라이브러리로 사용할 수 있습니다. (제작자 추천) 1. mylib 폴더에 넣기 2. Actions ➡️ library ➡️ refresh libraries 실행 하기 2025 10.29 ChatGPT-5 기호(÷, /, :) 자체는 의미적으로 같은 “나눗셈”을 뜻하지만, 문맥(사람이 쓰는 수학 vs 컴퓨터/프로그래밍)에 따라 해석 우선순위가 달라질 수 있습니다. 🔹 1️⃣ 전통 수학 표기 — ÷, /, : 수학 교과서, 논문, 일반 문서 등에서는 셋 다 의미적으로 “나누기”로 간주됩니다. 즉, 48÷2(9+3), 48/2(9+3), 48:2(9+3) 은 같은 의미로 받아들여야 합니다. 모두 사람의 수학 관행적 해석이 적용되어 48 ÷ 2 × (9+3) = 288 로 처리되죠. 즉, 기호가 바뀌어도 결과는 바뀌지 않습니다. 🔹 2️⃣ 컴퓨터·프로그래밍 문맥에서 / 사용 시 컴퓨터는 “생략된 곱셈(implicit multiplication)”을 따로 구분하지 못합니다. 따라서 다음 두 식은 완전히 다르게 인식됩니다. 표현 파이썬 등에서 해석 결과 48 / 2*(9+3) ((48 / 2) * (9+3)) 288 48 / 2(9+3) ❌ 문법 오류 (생략된 곱셈 인식 불가) — 즉, 컴퓨터 언어에서는 생략된 곱셈이 허용되지 않기 때문에, /는 반드시 명시적 *와 함께 써야 합니다. 🔹 3️⃣ “:” 기호의 경우 현대 수학에서는 “비율”을 나타내는 기호로 쓰입니다. a:b = \frac{a}{b} 따라서 (27 : 3(1+2)3) 같은 표현은 모호하거나 비표준적으로 간주됩니다. 대부분의 경우 계산기로는 입력 자체가 불가능합니다. ✅ 정리 기호 의미 결과 변화 주로 쓰이는 문맥 ÷ 나누기 없음 초중등 수학, 일반 표기 / 나누기 없음 (단, 프로그래밍에서는 생략 곱 불허) 수학/컴퓨터 : 비율 (또는 나누기 의미로 혼용) 보통 계산식에서는 사용 안 함 비, 비율 표기 🔹 결론 48 ÷ 2(9+3), 48/2(9+3), 48:2(9+3) 는 “수학적 의미”로는 동일하게 81로 해석됩니다. 하지만 프로그래밍이나 수식 파서(context) 에서는 /만 유효하고, 생략된 곱은 허용되지 않으며, :는 아예 다른 의미(비율)로 인식됩니다. 2025 10.28