- TI nspire
[TI-nspire] Fourier Transform Library 푸리에 변환 라이브러리 (ported from TI-92)
오리지널(TI-92/89) 라이브러리
https://allcalc.org/52455
Author: Lars Frederiksen
E-mail: LTF@POST8.TELE.DKPS. Please do not ask for more programs.
포팅 -  진행중
진행중
아무리 찾아봐도 TI-nspire 용 fourier transform 라이브러리(프로그램)이 없고,
TI-92/89 용으로는 단 하나 찾아지긴 했는데, 포팅하려고 보니 코드가 단순하지가 않네요.
진행 완료
- fourier() 함수 - libpub
- fouriersub() 함수
- ifourier() 함수 - libpub
- eval() 함수 - libpub
- phi() 함수 // 원본은 pi() 인데, 제한이 있어 변경함
- lambda() 함수
미진행
- Help Program
- Plot program
- Menu Program
프로그램 내부에서 변화된 내용
프로그램 구조가 바뀌지는 않았구요.
일부 변수명이 바뀌는 수준의 자잘한 변화가 있습니다.
1. Γ 를 변수명으로 사용시 소문자로 강제변환되기 때문에,
소문자 γ 를 쓸까하다가
대체문자 capital F, Fisher ideal index 를 사용하였습니다.
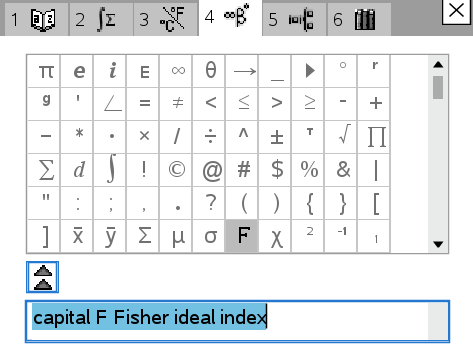
그런데, 단순히 변수문자로만 사용되는 것이 아니고, 코드 중간에 결합되어 쓰이는 부분도 있어서, 어떻게 해야 맞는 건지 감이 오지 않습니다.
ㄴ 다만, 이 코드는 Label test2 에 있는거라서 영향이 없는 건지도?
2. Δ 삼각형 심볼(increment or triangle)은 문자변수명에 사용할 수 없어서,
inc 라는 문자로 대체하였습니다.
3. TI-92에서는 대문자였던 변수는 그냥 소문자로 변하도록 자연스럽게 놔뒀습니다.
4. 그 외에는 최대한 원본과 동일한 모양을 유지하도록 하였습니다.
사용방법
1. tns 파일을 라이브러리에 넣고 ⇒ refresh 해줍니다.
※ 파일 다운로드는 본문 하단의 attatched file+ 에 있습니다.
2. fourier(함수,변수,결과형식타입) 으로 입력합니다.
3. 결과 형식 타입(모드)
├ 1 : 각속도 w 도메인. (exp(i*w) 형식이 cos(w)+i*sin(w)) 로 표시됩니다.
├ 2(추천) : 각속도 w 도메인. 복소수 기호 'i' 이, 알파벳 'i' 로 대신 표시됩니다. sin/cos 대신 지수형식으로 표시됩니다.
├ 3 : 주파수 f 도메인.
└ 4 : 주파수 f 도메인. 복소수 기호 'i' 이, 알파벳 'i' 로 대신 표시됩니다.
※ 일단 2로 해보고, 잘 안되거나, 맘에 안들면 1로 바꿔 보세요.
4. 특수 함수
- 유닛스텝함수 u() 는 알파벳 u 를 입력
- 델타함수는 카탈로그 - 특수문자 δ 를 입력
- signum() 은 알파벳으로 전체 입력
- 사각함수 rect(t/τ) 는 u(t+τ/2)-u(t-τ/2) 로 변환하여 입력 : 댓글 이미지 참고
※ 각각의 특수함수들은 문자로서 표시될 뿐, 함수로서 기능 하지는 않습니다.
댓글6
-
세상의모든계산기
예제2 : https://blog.naver.com/songsite123/222940646211
되는 것 (대충이라도 되는 것 포함)

-
1
세상의모든계산기
안되는 예제
- 절대값 입력시 변환 실패
- 변수(a, u 등)에 다른 값이 저장되어 있을 경우 오류 발생 가능. delvar 필요함.

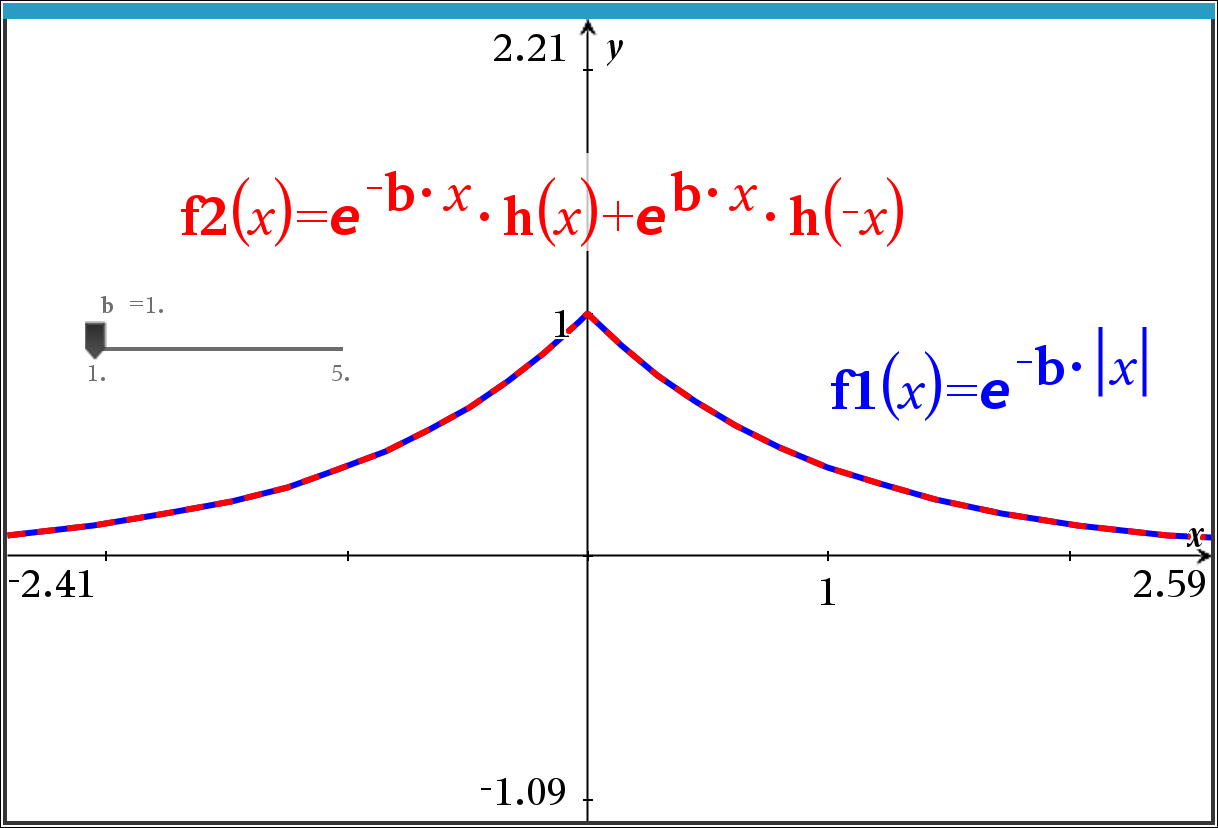
-
세상의모든계산기
예제3 : https://www.fmkorea.com/2952857872
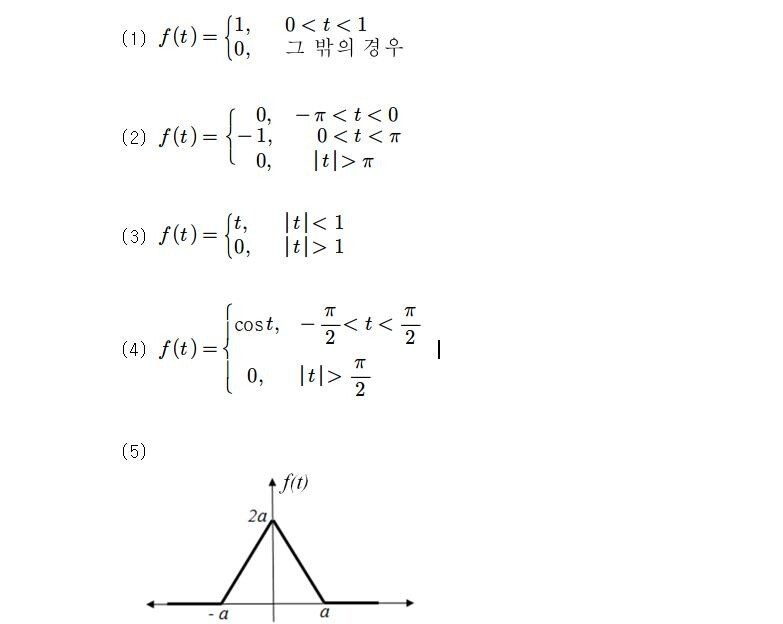
답변 : https://www.fmkorea.com/2953144342
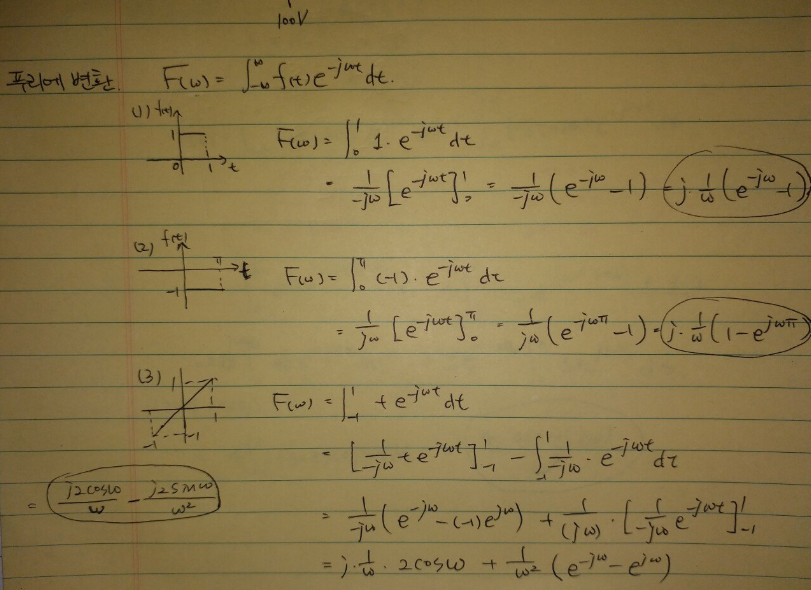

-
1
세상의모든계산기
되는 것
* u 변수를 할당하면 fourier()에서 에러가 나기 때문에, 그래프로 그려서 확인하기 위해 h(x) 를 다시 정의하였습니다. (fourier 변환에 필수요소는 아닙니다)
* w를 w_로 바꾸면 위의 풀이 결과와 제일 비슷하게 정리되어서 대체하였습니다. 필요에 따라 바꾸셔도 되고, 안바꾸셔도 됩니다.
* 결과 모드를 1로 할지, 2로 하고 i=@i 로 바꿀지는 알아서 판단해 보시기를...
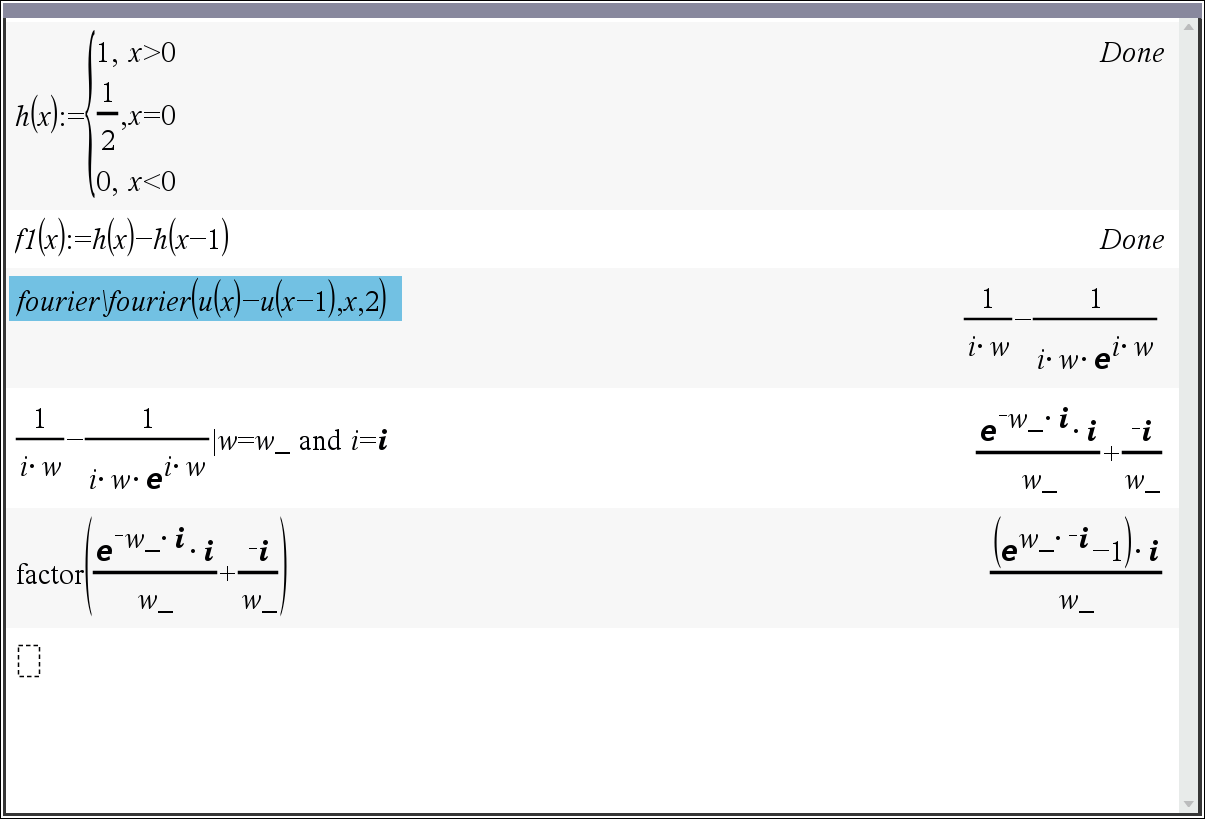
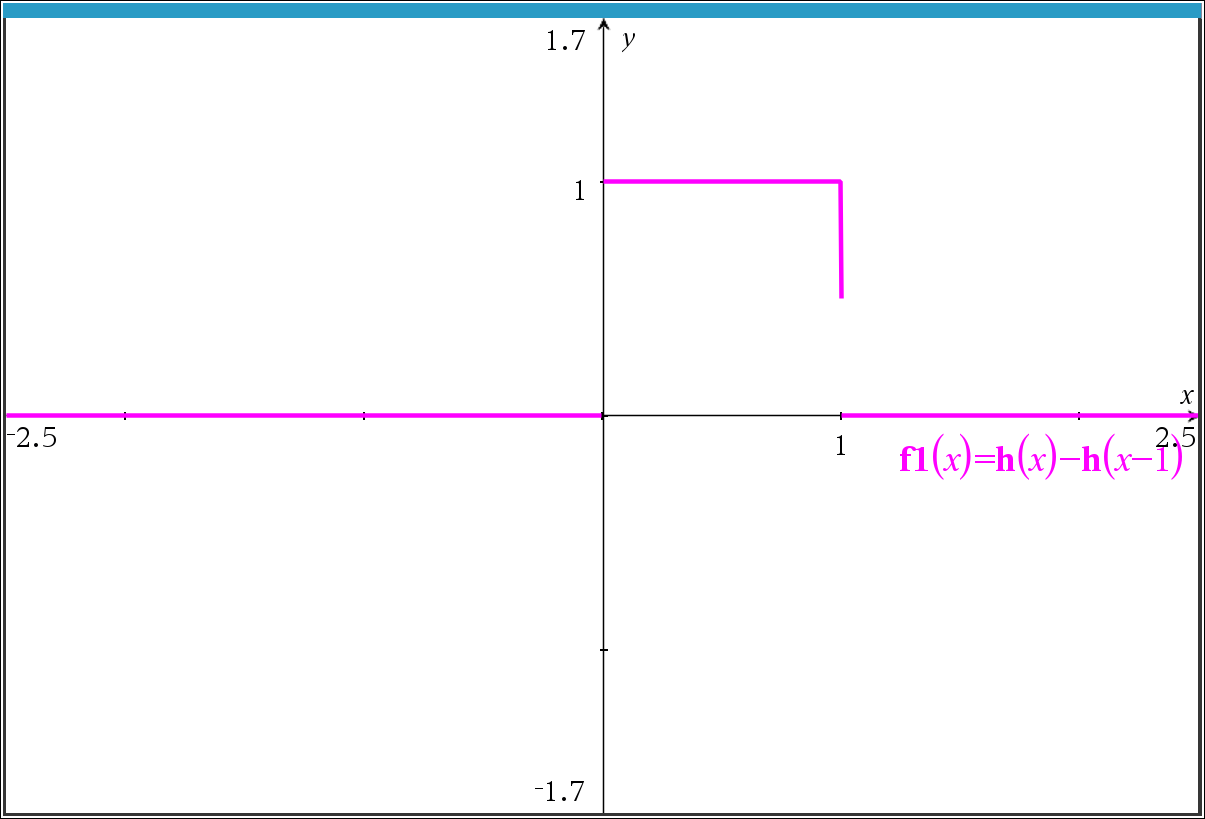
x=1 에서 y축 방향으로 0.5~1 사이에만 수직으로 직선이 표시되는데, 왜 표시되는지 모르겠습니다.
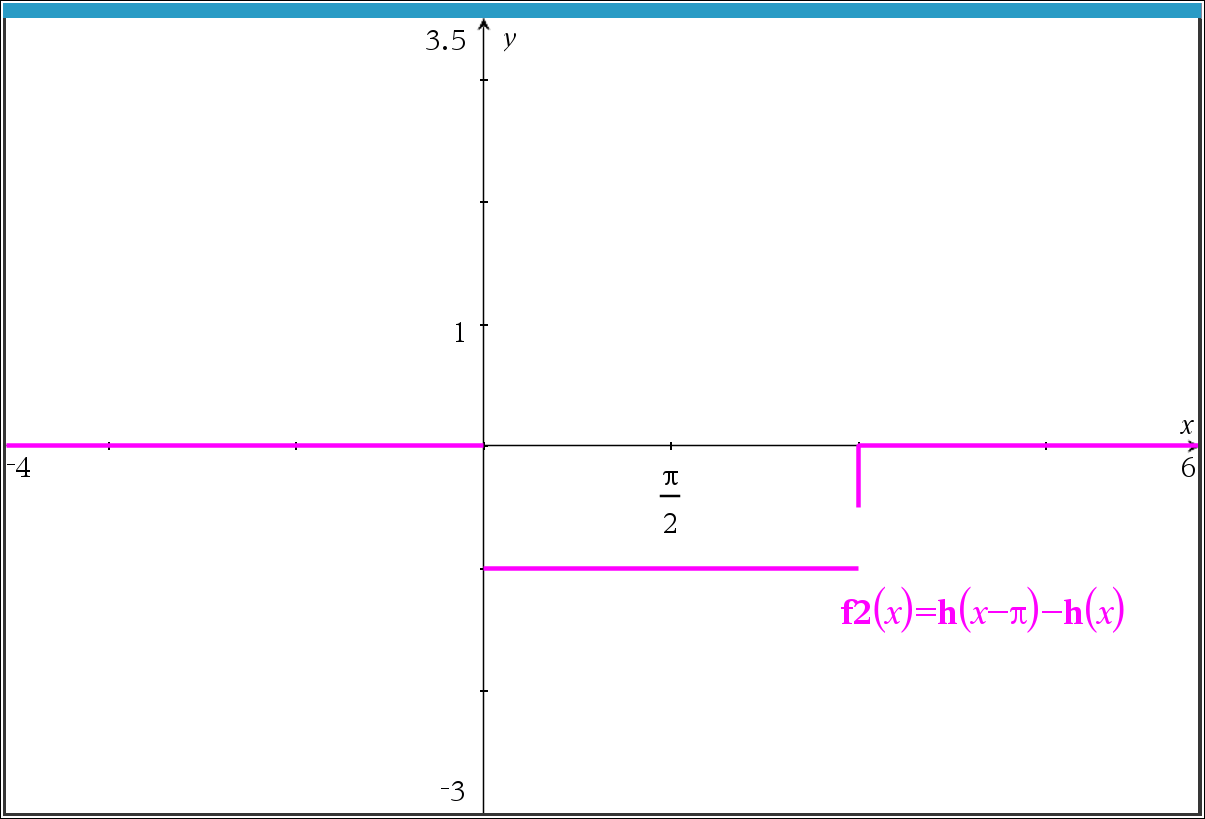
0~1 구간 전부 표시되면 더 좋겠지만, '아예 안보여도 할 말 없는데, 보이는 거니까" 이거라도 감지덕지겠지요.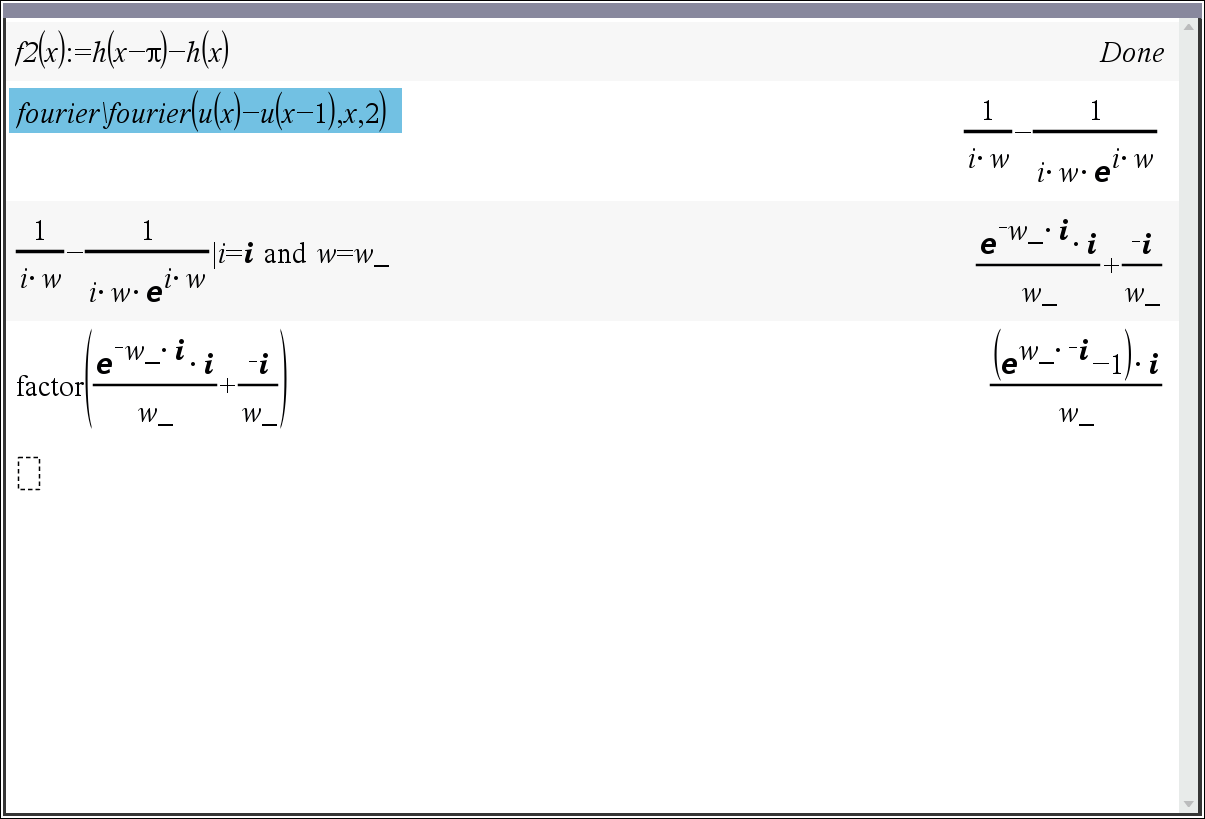

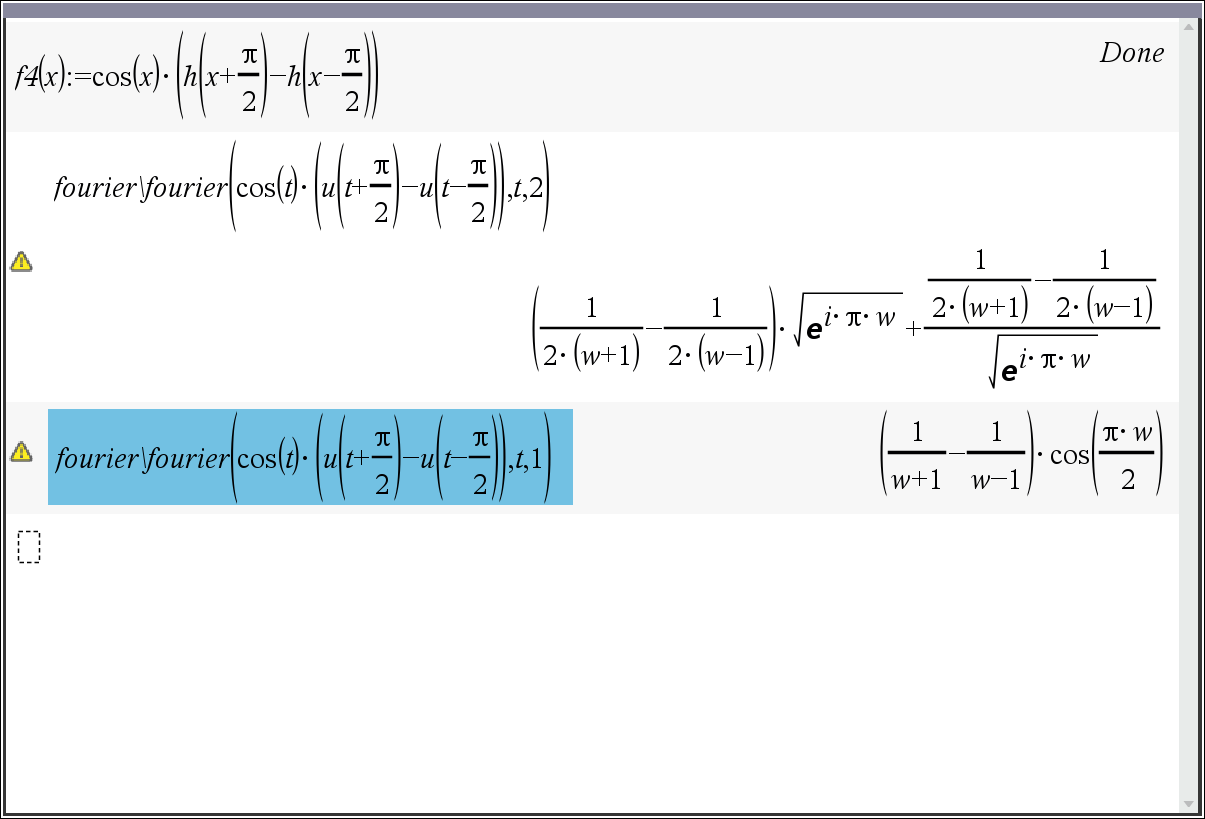
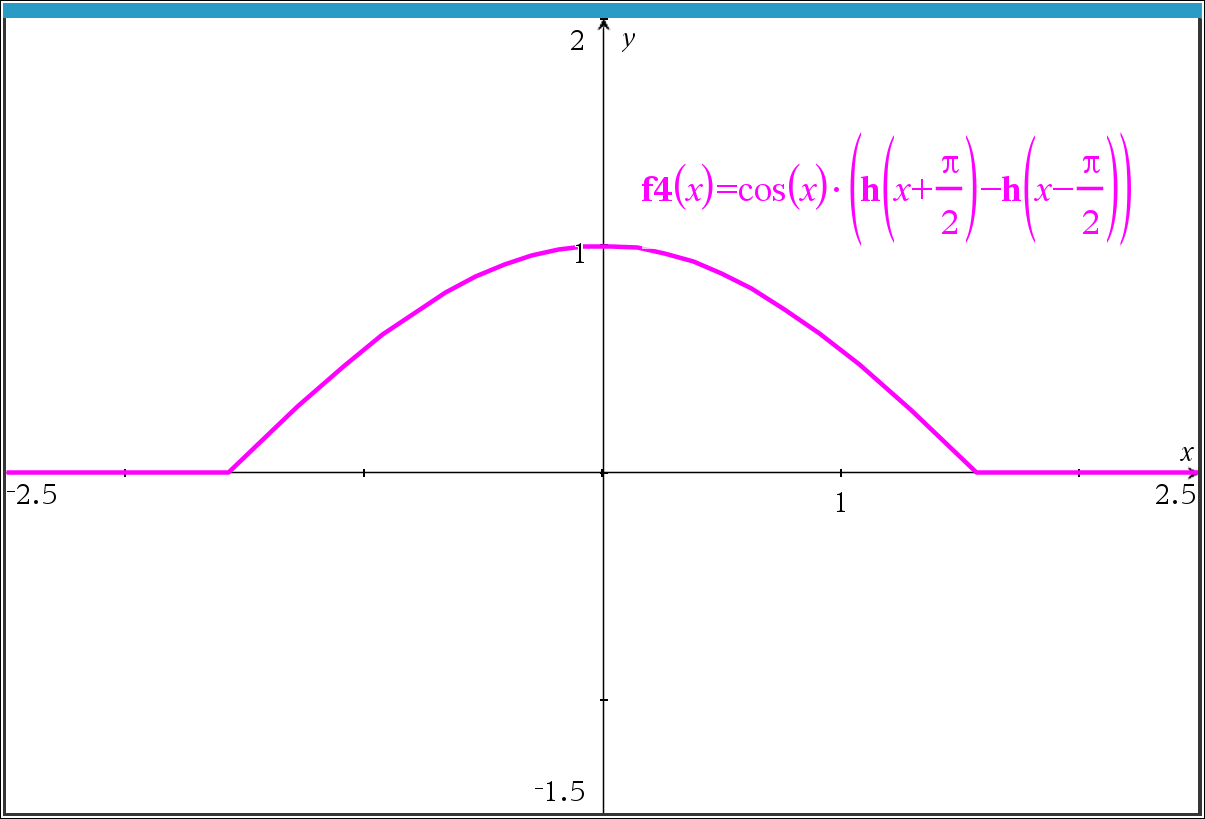
-
1
세상의모든계산기
안되는 것
* 절대값이 들어가면 무한루프에 빠지는 것 같습니다.
* 절대값을 풀어서 두 구간으로 나눈 다음에 더하면 되겠죠? 아마도???
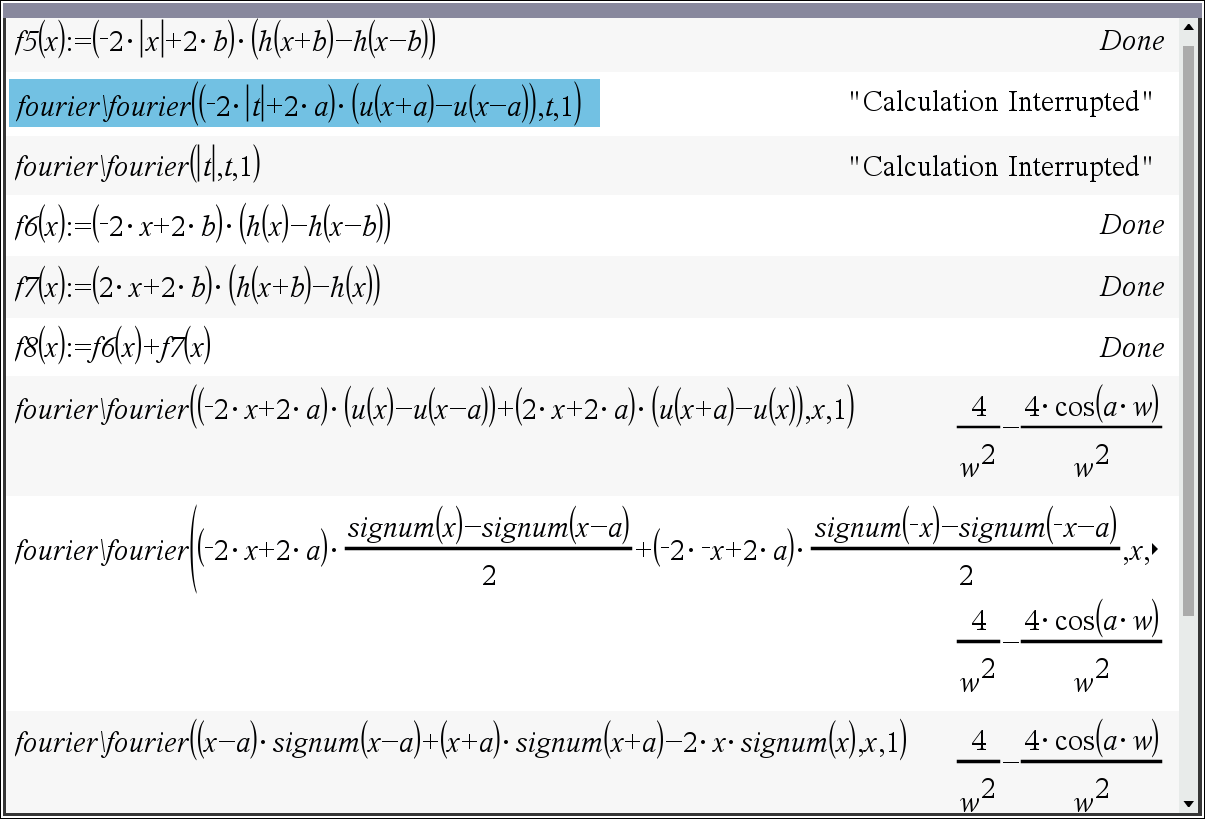
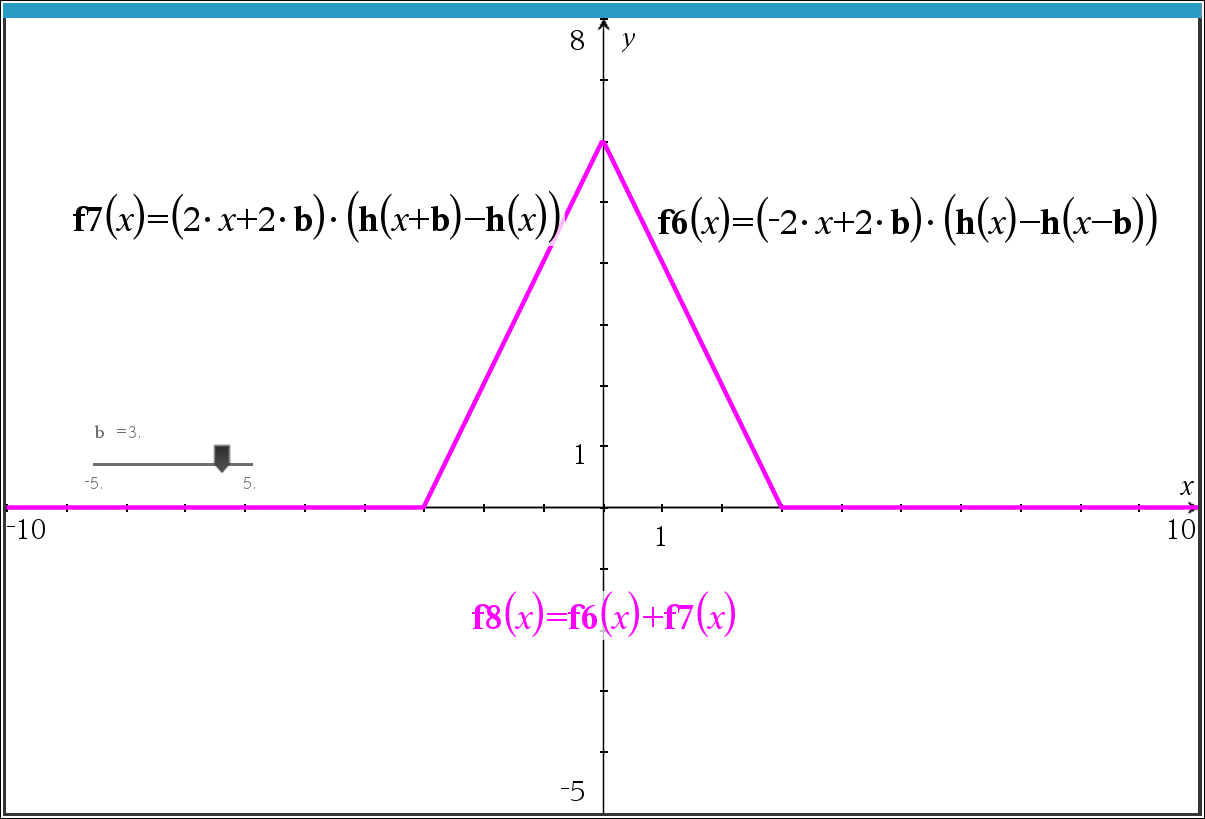
-
세상의모든계산기
ifourier
fourier() 만큼 복잡할 것으로 예상했는데,
예상과 달리 fouriersub() 를 활용해서 간단하게 처리하네요.

프로그램 설명 예제에는 (마지막 예시가) t 로 나와 있고, 결과가 sin(5t)/pi 로 되어 있지만, w로 바꿔야 에러가 나지 않고, 결과도 cos(5t)/pi 로 나옴.


세상의모든계산기 님의 최근 댓글
3×3 이상인 행렬의 행렬식 determinant https://allcalc.org/50536 2025 12.30 답에 이상한 숫자 14.2857142857가 들어간 것은 조건식에 소숫점(.) 이 들어가 있기 때문에 발생한 현상이구요. 100÷7 = 14.285714285714285714285714285714 소숫점 없이 분수로 식이 주어졌을 때와 결과적으로는 동일합니다. 2025 12.30 그럼 해가 무한히 많은지 아닌지 어떻게 아느냐? 고등학교 수학 교과과정에 나오는 행렬의 판별식(d, determinant)을 이용하면 알 수 있습니다. ㄴ 고교과정에서는 2x2 행렬만 다루던가요? 연립방정식의 계수들로 행렬을 만들고 그 행렬식(determinant)을 계산하여야 합니다. 행렬식이 d≠0 이면 유일한 해가 존재하고, d=0 이면 해가 없거나 무수히 많습니다. * 정상적인 경우 (`2y + 8z = 115`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 8 | 행렬식 값 = 1(0 - (-7)) - 1(8 - 0) = 7 - 8 = -1 (0이 아니므로 유일한 해 존재) * 문제가 된 경우 (`2y + 7z = 100`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 7 | 행렬식 값 = 1(0 - (-7)) - 1(7 - 0) = 7 - 7 = 0 (0이므로 유일한 해가 존재하지 않음) 2025 12.30 좀 더 수학적으로 말씀드리면 (AI Gemini 참고) 수학적 핵심 원리: 선형 독립성(Linear Independence) 3원 1차 연립방정식에서 미지수 x, y, z에 대한 단 하나의 해(a unique solution)가 존재하기 위한 필수 조건은 주어진 세 개의 방정식이 서로 선형 독립(linearly independent) 관계에 있어야 한다는 것입니다. * 선형 독립 (Linearly Independent): 어떤 방정식도 다른 방정식들의 조합(상수배를 더하거나 빼는 등)으로 만들어질 수 없는 상태입니다. 기하학적으로 이는 3개의 평면(각 방정식은 3D 공간의 평면을 나타냄)이 단 한 개의 점(해)에서 만나는 것을 의미합니다. * 선형 종속 (Linearly Dependent): 하나 이상의 방정식이 다른 방정식들의 조합으로 표현될 수 있는 상태입니다. 이 경우, 새로운 정보를 제공하지 못하는 '잉여' 방정식이 존재하는 것입니다. 기하학적으로 이는 3개의 평면이 하나의 선에서 만나거나(무수히 많은 해), 완전히 겹치거나, 혹은 평행하여 만나지 않는(해가 없음) 상태를 의미합니다. 질문자님의 사례는 '선형 종속'이 되어 무수히 많은 해가 발생하는 경우입니다. 2025 12.30 질문하신 연립 방정식은 미지수가 3개이고 모두 1차인 3원 1차 연립방정식입니다. 이상적으로 문제가 없다면 {x,y,z} 에 대한 좌표가 하나 나오게 됩니다. 원하는 답 {52.5, -2.5, 15} 그런데 두개 조건(식)을 그대로 두고 나머지 하나를 변형하다 보니 원하는 답이 나오지 않는 상황이 발생하였다고 질문하신 상황입니다. 3개의 조건식이 주어진 3원 1차 연립방정식은 조건을 변형해서 하나의 변수를 제거할 수 있습니다. 그러면 2개의 조건식으로 주어지는 2원 1차 연립방정식으로 변형할 수 있습니다. (알아보기 더 쉬워서 변형하는 겁니다) 변경하지 않은 조건의 식(con1) 을 이용해 하나의 y & z 1차 방정식을 유도할 수 있는데요. 나머지 방정식이 con1에서 유도된 방정식과 동일해지면 하나의 답이 구해지지 않는 것입니다. 계산기(ti-nspire)는 {x,y,z} 의 답이 하나가 아니고 무수히 많음을 c1 을 이용해서 표현해 준 것입니다. linear_independence_cond12.tns 2025 12.30