- TI nspire
[TI-nspire] 푸리에 급수, 내장함수 & 그래프로 확인하기 - 예제 #1
-
- 2024.11.15 - 22:34 2024.11.11 - 13:48 952 8
문제
함수 정의
\[
f(x) =
\begin{cases}
x + 1, & -1 < x < 0 \\
1 - x, & 0 \leq x < 1
\end{cases}
\]
이 함수 \( f(x) \)는 \(-1 < x < 1\)에서 정의되어 있으며, 주기 \( T = 2 \)를 가지도록 주기적으로 확장된다고 가정합니다. 즉, \( f(x + 2) = f(x) \)입니다.
목표
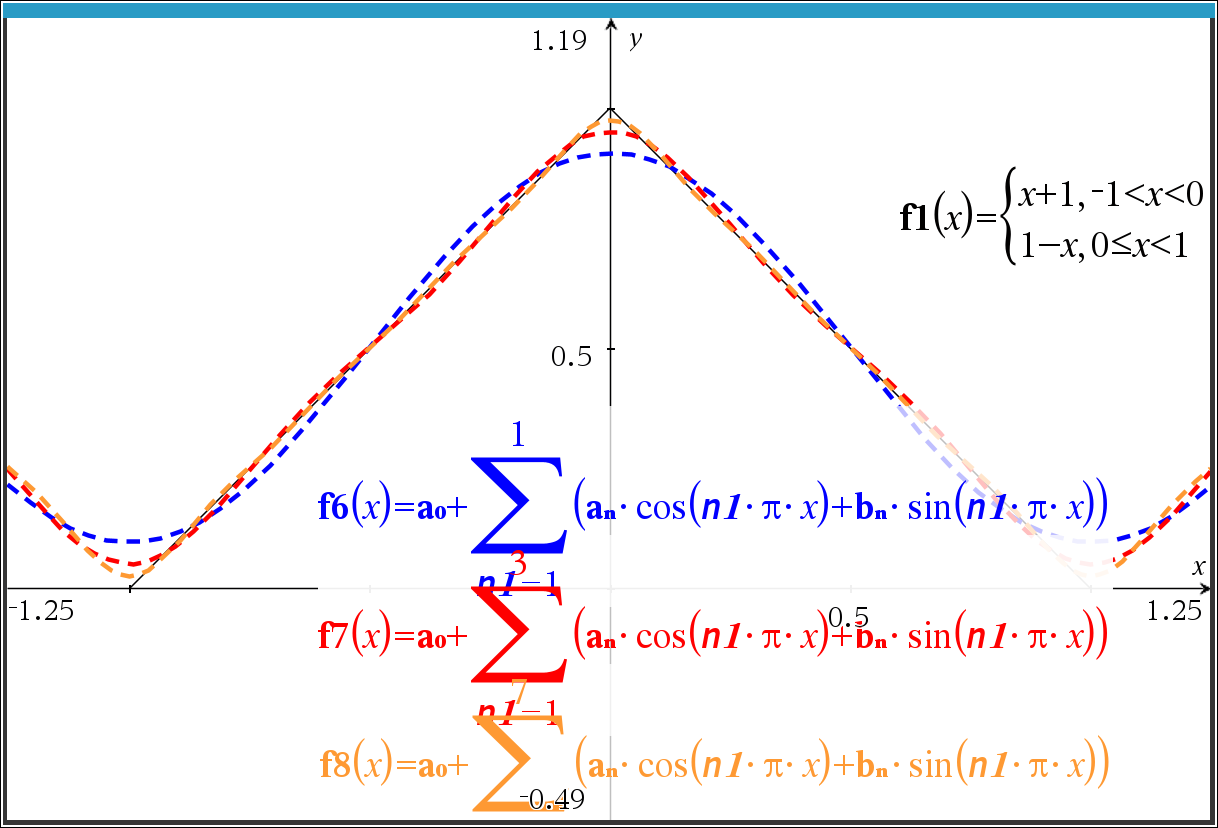
1. 함수 \( f(x) \)의 푸리에 급수를 계산하세요.
2. 푸리에 급수의 일반항을 구하고, 그 결과를 적어도 첫 몇 개의 항으로 나타내세요.
풀이 힌트
1. 주기 \( T = 2 \) 이므로, 기본 각주기는 \( \omega_0 = \frac{2\pi}{T} = \pi \) 입니다.
2. 함수 \( f(x) \)는 구간 \(-1 < x < 1\) 에서 정의되어 있으므로, 이 구간에서 푸리에 급수의 계수를 \( a_n \), \( b_n \) 계산해야 합니다.
푸리에 급수의 일반적인 표현은 다음과 같습니다:
\[
f(x) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos(n \pi x) + b_n \sin(n \pi x) \right)
\]
여기서:
- \( a_0 \)는 상수항,
- \( a_n \)과 \( b_n \)은 각각 코사인 및 사인 항의 계수로, 다음과 같이 정의됩니다:
\[
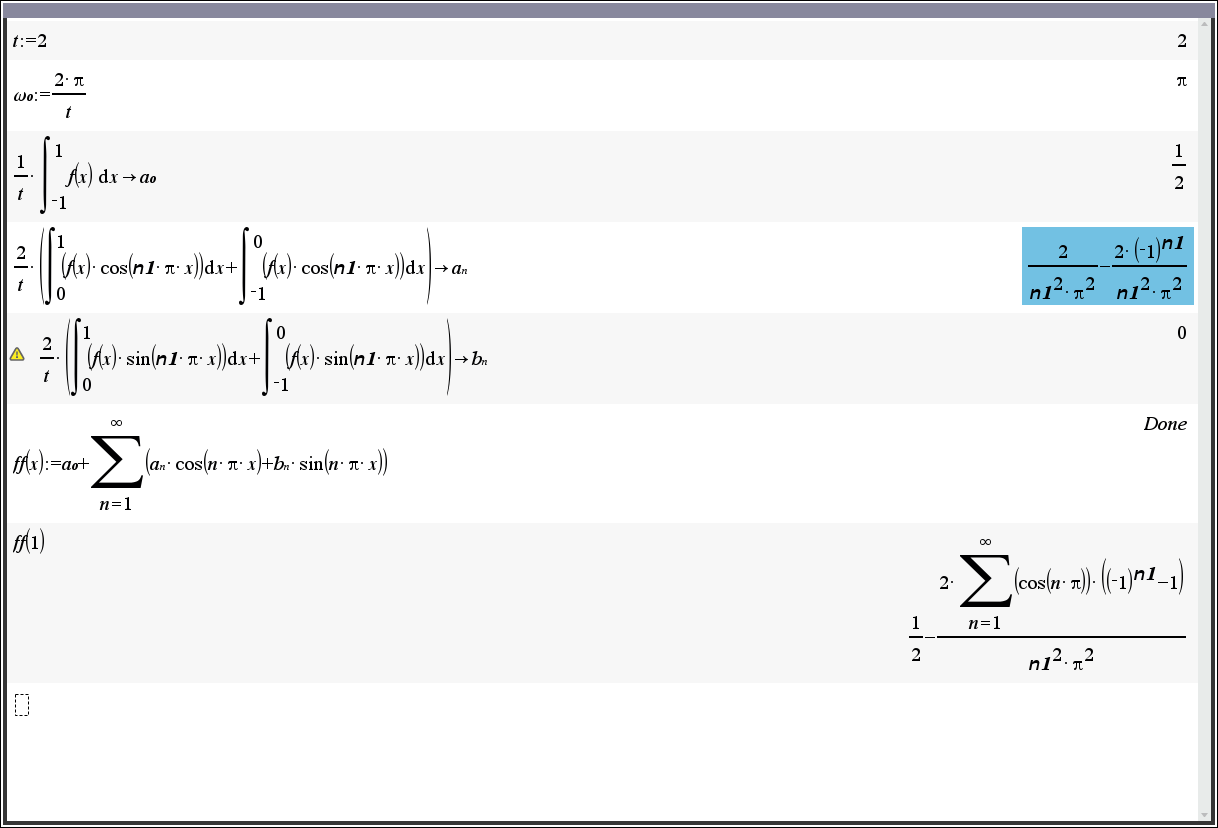
a_0 = \frac{1}{T} \int_{-1}^{1} f(x) \, dx
\]
\[
a_n = \frac{2}{T} \int_{-1}^{1} f(x) \cos(n \pi x) \, dx
\]
\[
b_n = \frac{2}{T} \int_{-1}^{1} f(x) \sin(n \pi x) \, dx
\]
각각의 계수를 구한 후, 푸리에 급수를 완성해 보세요.
-
25
댓글8
-
세상의모든계산기
1. 함수의 정의 / 정적분 확인
ㄴ
Sin 적분 경고 Warning : Domain of the result might be larger than the domain of the input.※ 이 문제에서 사용된 조각함수(Piecewise Continuous Function)는 단독으로는 적분도 되고, 미분도 되지만,
다른 함수와 결합되면(cos 함수와 곱해짐) 아쉽게도 Nspire 에서 직접 정적분되지 않습니다.
혹 정적분되더라도 approx(근사값)으로만 표시되며, 게다가 재수없으면 오류가 발생하는 경우도 있습니다.따라서 어쩔 수 없이 구간을 두 부분으로 나누어 계산하고 합쳐야 합니다.
ㄴ https://allcalc.org/52386 : [PDF] Convolution Integrals with Nspire CAS※ n 이 아니라 @n1 을 사용한 이유 : https://allcalc.org/5077 -
세상의모든계산기
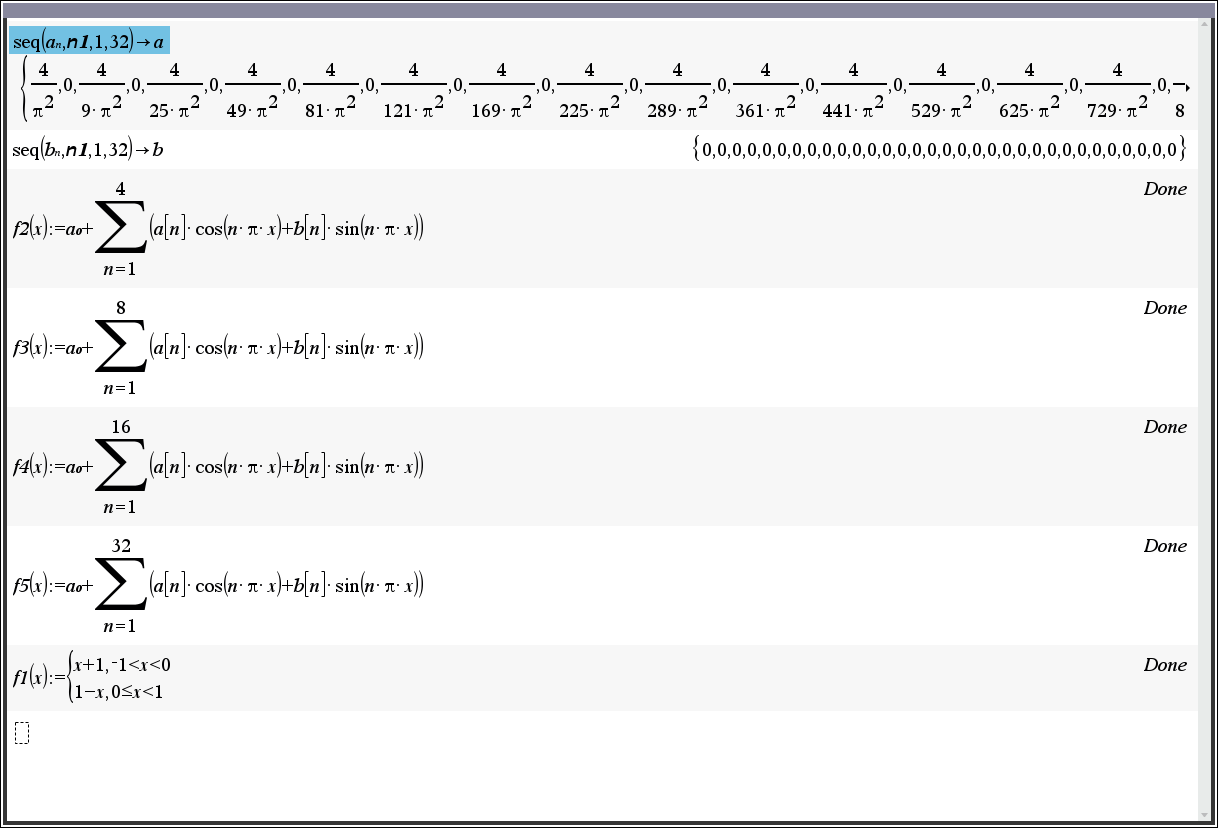
2. 상수항(a₀) / 계수(an, bn) - 일반항 정의
- 1
-
-
1
세상의모든계산기
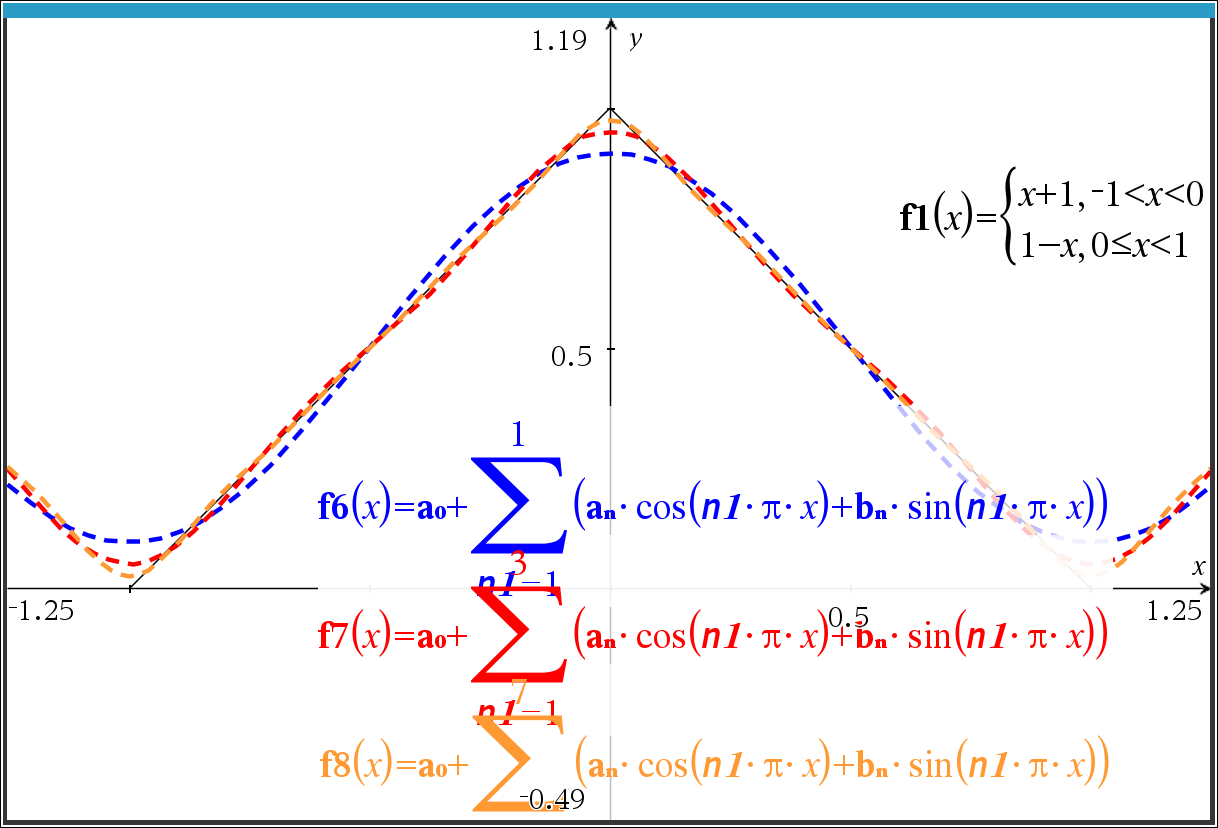
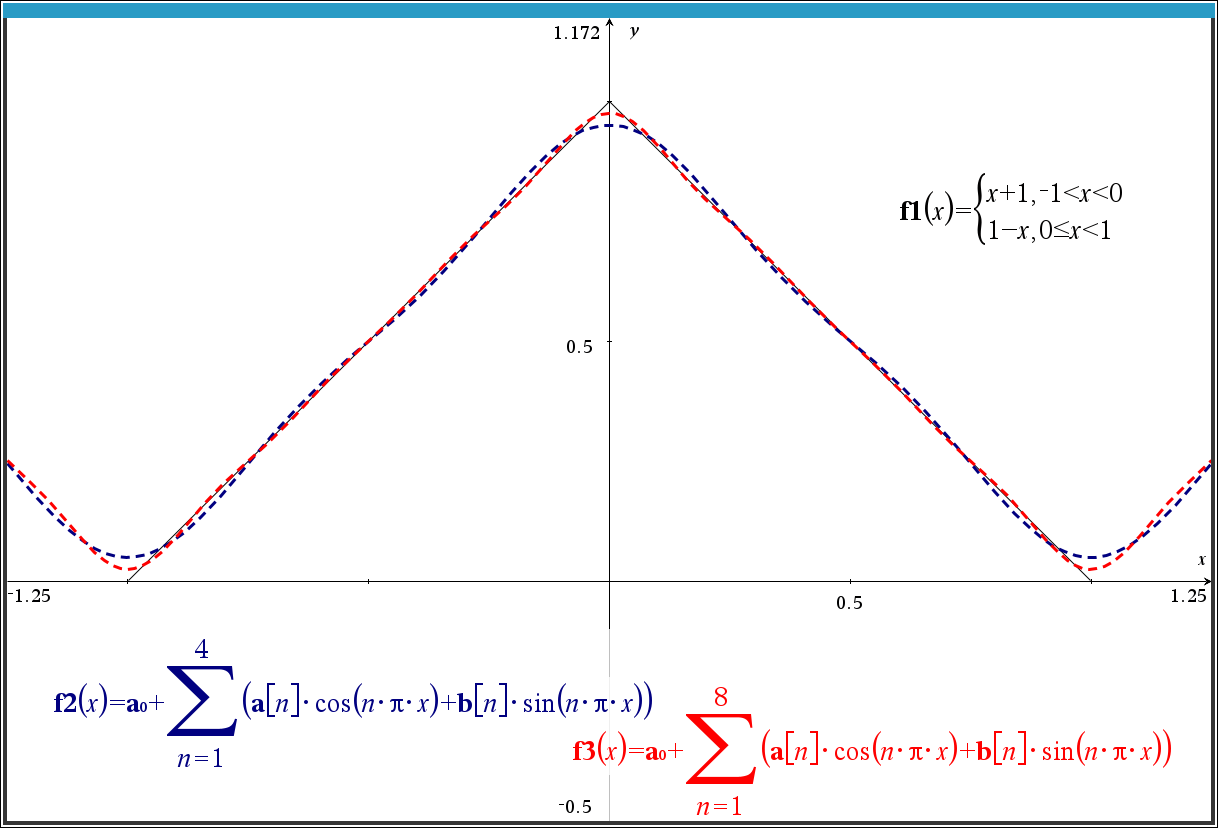
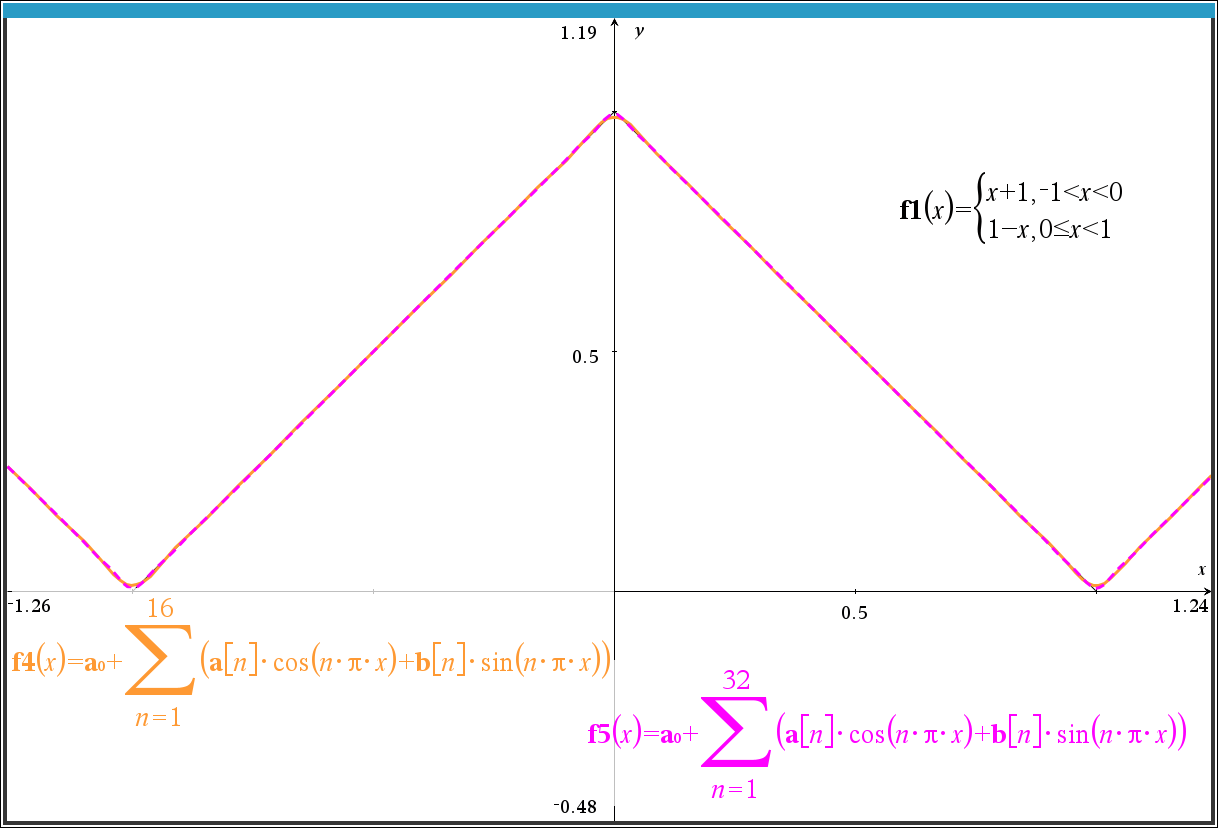
3.1 그래프 수식 입력 대안
seq() 함수로 list 를 생성하는 중간과정 없이, @n1 을 그대로 이용할 수도 있음.
- 1
-
-
세상의모든계산기
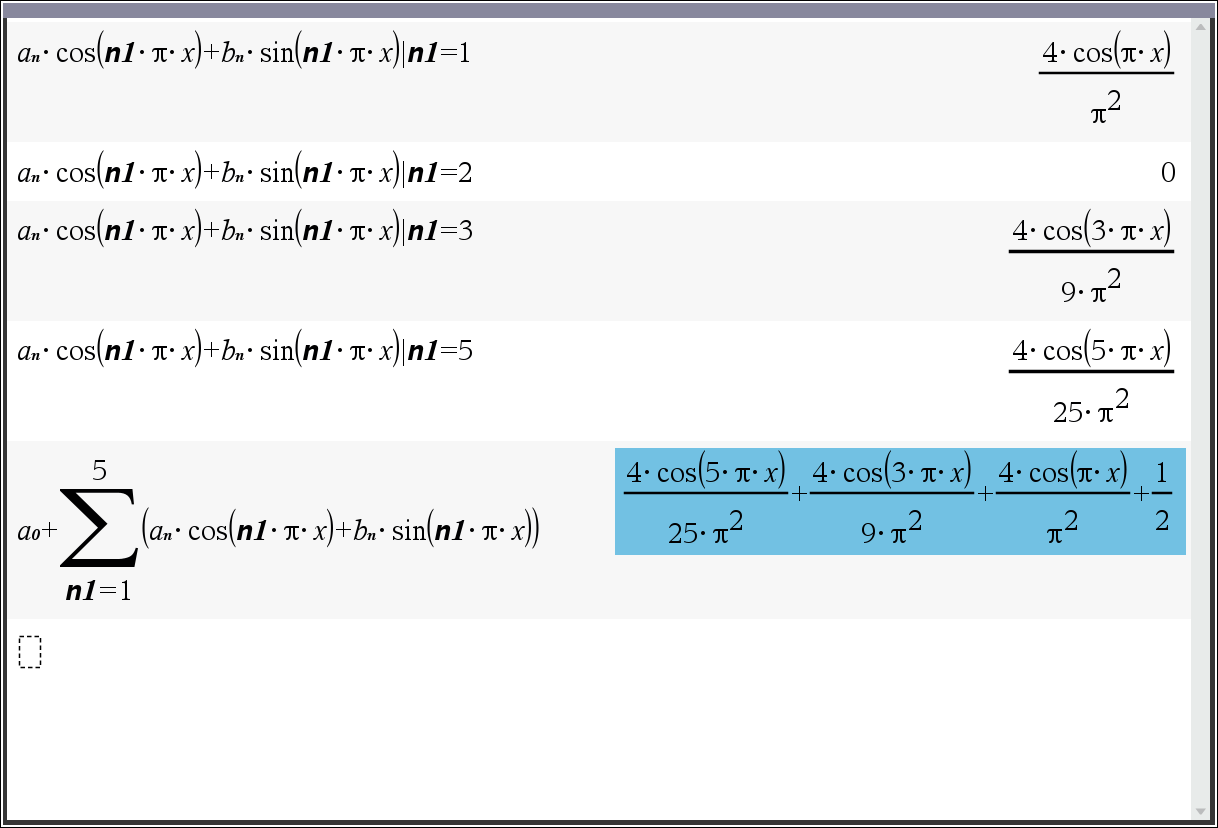
5. 라이브러리 kit_ets_mb\fourier() 사용시
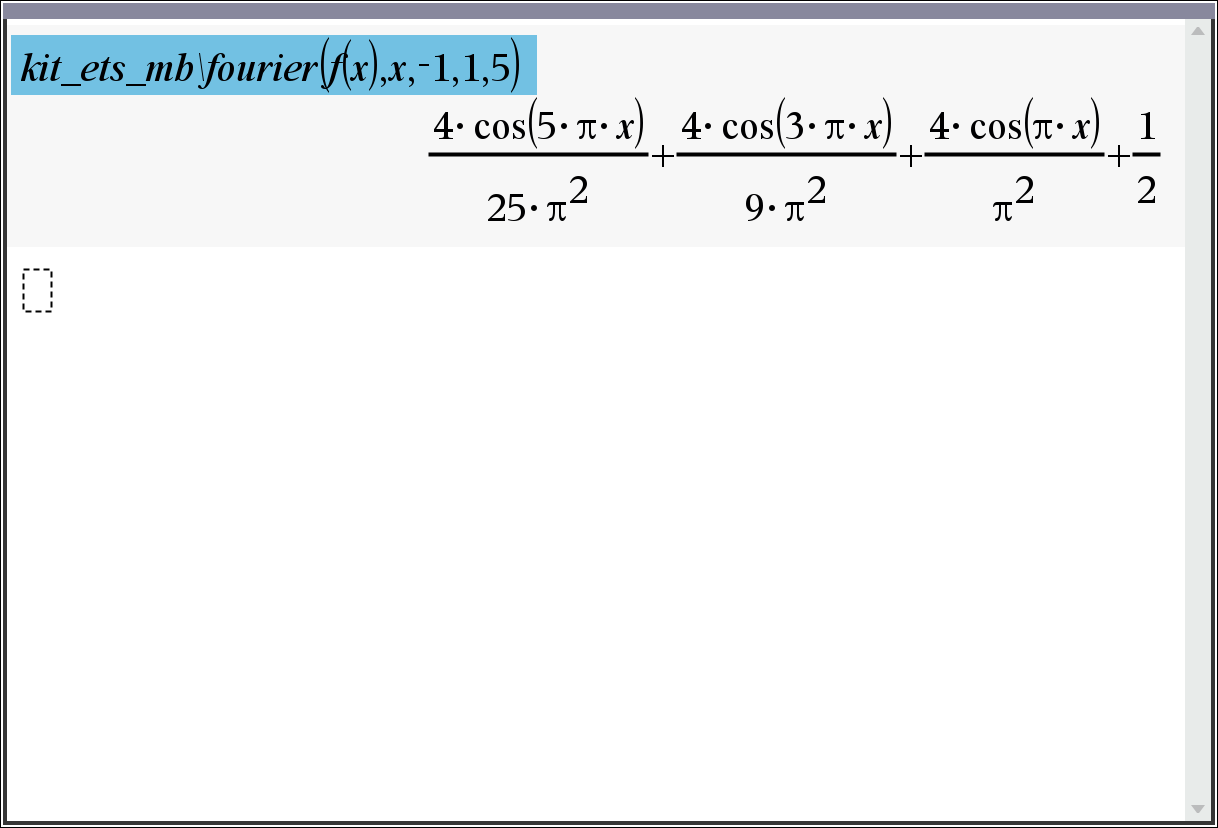
라이브러리 : https://allcalc.org/52395
세상의모든계산기 님의 최근 댓글
은행앱 통합하면서 없어졌나보네요. ㄴ 비슷한 기능 찾으시는 분은 : 스마트 금융 계산기 검색해 보세요. https://play.google.com/store/apps/details?id=com.moneta.android.monetacalculator 2026 01.25 Ctrl+Z 를 이용해 뒤로 돌아기기 Undo 기능이 있는지 살펴보세요. 2026 01.23 쌀집계산기로 연립방정식 계산하기 - 크래머/크레이머/크라메르 공식 적용 https://allcalc.org/56739 3. 'x' 값 구하기 계산기 조작법 목표: x = Dx / D = [(c×e) - (b×f)] / [(a×e) - (b×d)] 계산하기 1단계: 분모 D 계산 (메모리 활용) 1 * 1 M+ : 메모리(M)에 1를 더합니다. (현재 M = 1) -0.1 * -0.2 M- : 메모리(M)에서 0.02를 뺍니다. (현재 M = 0.98 = 0.98) 이로써 메모리(MR)에는 분모 0.98가 저장됩니다. 2단계: 분자 Dx 계산 후 나누기 78000 * 1 : 78000를 계산합니다. = : GT에 더합니다. -0.1 * 200000 : -20000를 계산합니다. ± = : 부호를 뒤집어 GT에 넣습니다. // sign changer 버튼 사용 GT : GT를 불러옵니다. GT는 98000 (분자 Dx) 값입니다. ÷ MR = : 위 결과(98000)를 메모리(MR)에 저장된 분모 D(0.98)로 나누어 최종 x값 100,000를 구합니다. 4. 'y' 값 구하기 계산기 조작법 목표: y = Dy / D = [(a×f) - (c×d)] / [(a×e) - (b×d)] 계산하기 1단계: 분모 D 계산 (메모리 활용) 'x'에서와 분모는 동일하고 메모리(MR)에 0.98가 저장되어 있으므로 패스합니다. 2단계: 분자 Dy 계산 후 나누기 GT ± = : GT를 불러오고 부호를 뒤집어 GT에 더합니다. GT가 0으로 리셋됩니다. 【AC】를 누르면 M은 유지되고 GT만 리셋되는 계산기도 있으니 확인해 보세요. 1 * 200000 : 200000를 계산합니다. = : GT에 더합니다. 78000 * -0.2 : -15600를 계산합니다. ± = : 부호를 뒤집어 GT에 넣습니다. GT : GT를 불러옵니다. 215600 (분자 Dy) 값입니다. ÷ MR = : 위 결과(215600)를 메모리(MR)에 저장된 분모 D(0.98)로 나누어 최종 y값 220,000를 구합니다. x, y 값을 이용해 최종 결과를 구합니다. 2026 01.18 크레이머 = 크레머 = 크라메르 공식 = Cramer's Rule https://allcalc.org/8985 2026 01.18 부호 변경, Sign Changer 버튼 https://allcalc.org/52092 2026 01.18