- TI nspire
[TI-nspire] 통계, (모평균의) 신뢰 구간 구하는 방법(예제). Statistics - Confidence Intervals
1. 다음 샘플의 모평균에 대한 95% 신뢰구간을 추정하시오.
샘플 = {20,20,25,21,21,23,19,18,22}
문제 출처 : http://math7.tistory.com/66
2. 기본 통계값을 구함 (생략하고 3으로 뛰어도 됨)
【menu】【6】【1】【1】 : One Variable Statistics
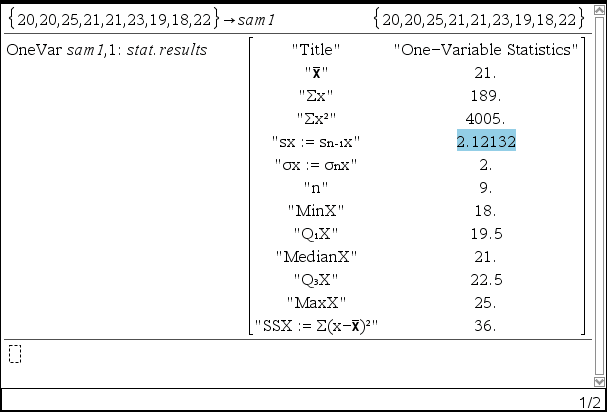
3. 신뢰구간 Confidence Intervals 을 구함

- tInterval 프로그램은 DATA 를 직접 이용할 수도 있고, 통계값을 이용할 수도 있다.
tInterval List [, Freq [, CLevel ]]
(Data list input)
tInterval , sx, n[, CLevel]
(Summary stats input)
- 신뢰구간에 대한 요약된 결과는 stat.results 에 저장된다.
다른 통계 프로그램이 사용하는 변수명과 동일하므로 overwrite 될 수 있다.
- sx는 모편차(σx)가 아닌, 표본의 편차임에 주의하자.
- 변수명
Output variableDescriptionstat.CLower, stat.CUpperConfidence interval for an unknown population meanstat.$\overline{x}$Sample mean of the data sequence from the normal random distributionstat.MEMargin of errorstat.dfDegrees of freedomstat.σxSample standard deviationstat.nLength of the data sequence with sample mean
댓글4
-
-
세상의모든계산기
Sample DATA가 아니라, 통계치가 주어졌을 때
문제:
어느 회사에서 전자기기용 부품인 힌지를 만들고 있습니다.
생산 라인은 안정화되어, 샘플 테스트시 고장이 발생할 때까지 접힐 수 있는 횟수는 정규 분포를 이룹니다.
평균 접히는 횟수는 25만번이고, 표준편차는 2만번으로 나타났습니다.
이번 Lot 생산품중 100개의 샘플을 수거하여 조사하였을 때
제품이 고장날 때까지 접힐 수 있는 평균 횟수의 95% 신뢰구간을 구하세요.
주어진 값
- 모집단 평균 (\(\mu\)): 250,000
- 모집단 표준편차 (\(\sigma\)): 20,000
- 샘플 크기 (\(n\)): 100
- 신뢰수준 = 95% (\( Z = 1.96 \))풀이
1. 표준 오차 (Standard Error, SE) 계산:
$ SE = \dfrac{\sigma}{\sqrt{n}} = \dfrac{20,000}{\sqrt{100}} = \dfrac{20,000}{10} \approx 2,000 $2. 95% 신뢰구간 계산: \[
\text{신뢰 구간} = \bar{X} \pm z_{\alpha/2} \times SE
\]
여기서 \(\bar{X} = \mu = 250,000\)이므로,
\[
\text{신뢰 구간} = 250000 \pm 1.96 \times 2000
\]3. 결과:
$ \text{95% 신뢰구간} = (246080, 253920) $ -
1
세상의모든계산기
6: Statistics - 6: Confidence Intervals - 1: z Interval

Data Input method : Stats

(Data list input) zInterval σ,List[,Freq[,CLevel]]
(Summary stats input) zInterval σ,$ \overline{x} $,n [,CLevel]

-
세상의모든계산기
z-interval vs t-interval 차이점
통계 프로그램에서 t-interval과 z-interval은 모집단의 평균을 추정할 때 사용하는 신뢰 구간 계산 방법으로, 모집단의 분산(또는 표준편차) 정보 유무와 표본 크기에 따라 선택됩니다.
1. z-interval (Z 신뢰 구간)
- 사용 조건: 모집단의 표준편차(\(\sigma\))를 알고 있을 때 사용합니다.
- 표본 크기 요건: 일반적으로 표본 크기가 충분히 큰 경우(보통 \( n \geq 30 \))에 사용하면 정규분포에 가깝게 추정할 수 있습니다.
- 계산: 신뢰 구간의 한계는 표준 정규분포를 이용해 계산됩니다.
- 예: \( \text{z-interval} = \bar{X} \pm Z_{\alpha/2} \times \frac{\sigma}{\sqrt{n}} \)2. t-interval (T 신뢰 구간)
- 사용 조건: 모집단의 표준편차를 모르는 경우 사용하며, 표본 표준편차(\(s\))를 대신 사용합니다.
- 표본 크기 요건: 표본 크기가 작을 때(보통 \( n < 30 \)) 또는 모집단의 분산을 알 수 없을 때 주로 사용됩니다.
- 계산: 신뢰 구간의 한계는 t-분포를 이용해 계산합니다. 이때 자유도(\(n-1\))가 필요합니다.
- 예: \( \text{t-interval} = \bar{X} \pm t_{\alpha/2, \, n-1} \times \frac{s}{\sqrt{n}} \)


세상의모든계산기 님의 최근 댓글
991CW+ KR 버전이 나오면, 그 때는 (어쩔 수 없이) CW 를 추천하게 될지도 모르겠습니다. 2026 01.14 참고리뷰 : https://www.reddit.com/r/calculators/comments/1o7kj7f/casio_fx9910cw_review_a_much_needed_improvement/ 카시오 FX-9910CW 리뷰: 절실히 필요했던 개선이지만… 너무 늦은 감이 있는 걸까? 2026 01.13 기사 시험 용도 - EX든 CW든 뭘 쓰셔도 점수에는 영향이 없음. - 선택기준 1 : 과거에 fx-570ES Plus 을 써 봤다 -> EX 추천 - 선택기준 2 : 주변에 ES 또는 EX 계산기 사용법 알려줄 사람이 있다 -> EX 추천 // CW도 마찬가지 - 선택기준 3 : EX 정품을 높지 않은 가격으로 구하는데 문제가 없다? -> EX 추천 // EX 단종 이슈 + 짝퉁 이슈 있음. - 선택기준 4 : 모험을 좋아한다 -> CW 추천 참고 https://gall.dcinside.com/mgallery/board/view/?id=calc&no=312 2026 01.13 fx-9910CW 한국 출시관련 정보는 없습니다. 2026 01.13 기간을 넉넉하게 잡고 봐야 할 듯 싶구요. 기다려 본 결과... '실패함'이 떴습니다. 잘 된건지 잘 못된 건지 아무 변화가 없는건지... 뭐가 뭔지 모르겠네요. 2026 01.03