- TI nspire
[TI-nspire] 통계, (모평균의) 신뢰 구간 구하는 방법(예제). Statistics - Confidence Intervals
1. 다음 샘플의 모평균에 대한 95% 신뢰구간을 추정하시오.
샘플 = {20,20,25,21,21,23,19,18,22}
문제 출처 : http://math7.tistory.com/66
2. 기본 통계값을 구함 (생략하고 3으로 뛰어도 됨)
【menu】【6】【1】【1】 : One Variable Statistics
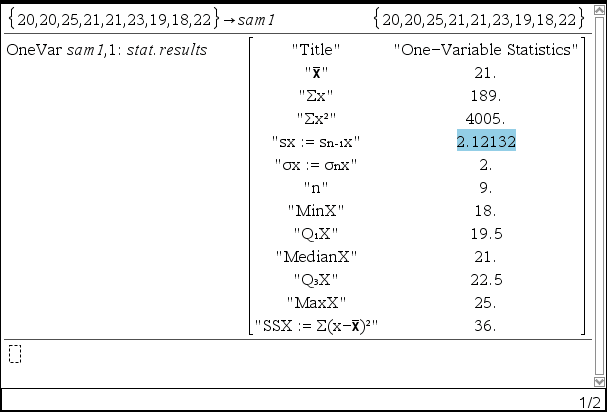
3. 신뢰구간 Confidence Intervals 을 구함

- tInterval 프로그램은 DATA 를 직접 이용할 수도 있고, 통계값을 이용할 수도 있다.
tInterval List [, Freq [, CLevel ]]
(Data list input)
tInterval , sx, n[, CLevel]
(Summary stats input)
- 신뢰구간에 대한 요약된 결과는 stat.results 에 저장된다.
다른 통계 프로그램이 사용하는 변수명과 동일하므로 overwrite 될 수 있다.
- sx는 모편차(σx)가 아닌, 표본의 편차임에 주의하자.
- 변수명
Output variableDescriptionstat.CLower, stat.CUpperConfidence interval for an unknown population meanstat.$\overline{x}$Sample mean of the data sequence from the normal random distributionstat.MEMargin of errorstat.dfDegrees of freedomstat.σxSample standard deviationstat.nLength of the data sequence with sample mean
댓글4
-
-
세상의모든계산기
Sample DATA가 아니라, 통계치가 주어졌을 때
문제:
어느 회사에서 전자기기용 부품인 힌지를 만들고 있습니다.
생산 라인은 안정화되어, 샘플 테스트시 고장이 발생할 때까지 접힐 수 있는 횟수는 정규 분포를 이룹니다.
평균 접히는 횟수는 25만번이고, 표준편차는 2만번으로 나타났습니다.
이번 Lot 생산품중 100개의 샘플을 수거하여 조사하였을 때
제품이 고장날 때까지 접힐 수 있는 평균 횟수의 95% 신뢰구간을 구하세요.
주어진 값
- 모집단 평균 (\(\mu\)): 250,000
- 모집단 표준편차 (\(\sigma\)): 20,000
- 샘플 크기 (\(n\)): 100
- 신뢰수준 = 95% (\( Z = 1.96 \))풀이
1. 표준 오차 (Standard Error, SE) 계산:
$ SE = \dfrac{\sigma}{\sqrt{n}} = \dfrac{20,000}{\sqrt{100}} = \dfrac{20,000}{10} \approx 2,000 $2. 95% 신뢰구간 계산: \[
\text{신뢰 구간} = \bar{X} \pm z_{\alpha/2} \times SE
\]
여기서 \(\bar{X} = \mu = 250,000\)이므로,
\[
\text{신뢰 구간} = 250000 \pm 1.96 \times 2000
\]3. 결과:
$ \text{95% 신뢰구간} = (246080, 253920) $ -
1
세상의모든계산기
6: Statistics - 6: Confidence Intervals - 1: z Interval

Data Input method : Stats

(Data list input) zInterval σ,List[,Freq[,CLevel]]
(Summary stats input) zInterval σ,$ \overline{x} $,n [,CLevel]

-
세상의모든계산기
z-interval vs t-interval 차이점
통계 프로그램에서 t-interval과 z-interval은 모집단의 평균을 추정할 때 사용하는 신뢰 구간 계산 방법으로, 모집단의 분산(또는 표준편차) 정보 유무와 표본 크기에 따라 선택됩니다.
1. z-interval (Z 신뢰 구간)
- 사용 조건: 모집단의 표준편차(\(\sigma\))를 알고 있을 때 사용합니다.
- 표본 크기 요건: 일반적으로 표본 크기가 충분히 큰 경우(보통 \( n \geq 30 \))에 사용하면 정규분포에 가깝게 추정할 수 있습니다.
- 계산: 신뢰 구간의 한계는 표준 정규분포를 이용해 계산됩니다.
- 예: \( \text{z-interval} = \bar{X} \pm Z_{\alpha/2} \times \frac{\sigma}{\sqrt{n}} \)2. t-interval (T 신뢰 구간)
- 사용 조건: 모집단의 표준편차를 모르는 경우 사용하며, 표본 표준편차(\(s\))를 대신 사용합니다.
- 표본 크기 요건: 표본 크기가 작을 때(보통 \( n < 30 \)) 또는 모집단의 분산을 알 수 없을 때 주로 사용됩니다.
- 계산: 신뢰 구간의 한계는 t-분포를 이용해 계산합니다. 이때 자유도(\(n-1\))가 필요합니다.
- 예: \( \text{t-interval} = \bar{X} \pm t_{\alpha/2, \, n-1} \times \frac{s}{\sqrt{n}} \)


세상의모든계산기 님의 최근 댓글
참고 : 라플라스 해법 1- 문제풀이의 개요 [출처] 라플라스 해법 1- 문제풀이의 개요|작성자 공학 엔지니어 지망생 https://blog.naver.com/hgengineer/220380176222 2026 01.01 3×3 이상인 행렬의 행렬식 determinant https://allcalc.org/50536 2025 12.30 답에 이상한 숫자 14.2857142857가 들어간 것은 조건식에 소숫점(.) 이 들어가 있기 때문에 발생한 현상이구요. 100÷7 = 14.285714285714285714285714285714 소숫점 없이 분수로 식이 주어졌을 때와 결과적으로는 동일합니다. 2025 12.30 그럼 해가 무한히 많은지 아닌지 어떻게 아느냐? 고등학교 수학 교과과정에 나오는 행렬의 판별식(d, determinant)을 이용하면 알 수 있습니다. ㄴ 고교과정에서는 2x2 행렬만 다루던가요? 연립방정식의 계수들로 행렬을 만들고 그 행렬식(determinant)을 계산하여야 합니다. 행렬식이 d≠0 이면 유일한 해가 존재하고, d=0 이면 해가 없거나 무수히 많습니다. * 정상적인 경우 (`2y + 8z = 115`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 8 | 행렬식 값 = 1(0 - (-7)) - 1(8 - 0) = 7 - 8 = -1 (0이 아니므로 유일한 해 존재) * 문제가 된 경우 (`2y + 7z = 100`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 7 | 행렬식 값 = 1(0 - (-7)) - 1(7 - 0) = 7 - 7 = 0 (0이므로 유일한 해가 존재하지 않음) 2025 12.30 좀 더 수학적으로 말씀드리면 (AI Gemini 참고) 수학적 핵심 원리: 선형 독립성(Linear Independence) 3원 1차 연립방정식에서 미지수 x, y, z에 대한 단 하나의 해(a unique solution)가 존재하기 위한 필수 조건은 '주어진 세 개의 방정식이 서로 선형 독립(linearly independent) 관계에 있어야 한다'는 것입니다. * 선형 독립 (Linearly Independent): 어떤 방정식도 다른 방정식들의 조합(상수배를 더하거나 빼는 등)으로 만들어질 수 없는 상태입니다. 기하학적으로 이는 3개의 평면(각 방정식은 3D 공간의 평면을 나타냄)이 단 한 개의 점(해)에서 만나는 것을 의미합니다. * 선형 종속 (Linearly Dependent): 하나 이상의 방정식이 다른 방정식들의 조합으로 표현될 수 있는 상태입니다. 이 경우, 새로운 정보를 제공하지 못하는 '잉여' 방정식이 존재하는 것입니다. 기하학적으로 이는 3개의 평면이 하나의 선에서 만나거나(무수히 많은 해), 완전히 겹치거나, 혹은 평행하여 만나지 않는(해가 없음) 상태를 의미합니다. 질문자님의 사례는 '선형 종속'이 되어 무수히 많은 해가 발생하는 경우입니다. 2025 12.30