- CASIO 570
[fx-570ES] STAT 통계 - 편차제곱의 합. SSX 또는 SSY
편차제곱의 합은 통계학에서 데이터의 분산과 표준편차를 계산할 때 중요한 개념입니다. 이를 이해하기 위해 먼저 편차를 정의해야 합니다.

1. 편차 (Deviation):
편차는 각 데이터 값이 평균에서 얼마나 떨어져 있는지를 나타내는 값입니다. 수식으로는 다음과 같습니다.
\[
\text{편차} = x_i - \mu
\]
여기서:
- \( x_i \)는 각 데이터 값
- \( \mu \)는 데이터 값들의 평균입니다.
2. 편차제곱 (Squared Deviation):
편차는 양수 또는 음수일 수 있기 때문에, 이 값들을 제곱하여 편차제곱을 구합니다. 이는 음수와 양수를 구분하지 않고 편차의 크기만을 평가할 수 있게 합니다.
\[
\text{편차제곱} = (x_i - \mu)^2
\]
3. 편차제곱의 합 (Sum of Squared Deviations):
편차제곱을 모든 데이터에 대해 구한 후, 이들을 모두 더한 값이 편차제곱의 합입니다. 이는 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내는 중요한 값입니다.
\[
\text{편차제곱의 합} = \sum_{i=1}^{n} (x_i - \mu)^2
\]
이 값은 분산(Variance) 및 표준편차(Standard Deviation)를 구하는 데 사용됩니다.
- 분산은 편차제곱의 합을 데이터 개수로 나눈 값입니다.
- 표준편차는 분산의 제곱근입니다.
- 약어 표시
- SSX: 독립 변수 XXX에 대한 편차제곱의 합 (Sum of Squares for XXX).
- SST: 총 편차제곱의 합 (Total Sum of Squares).
- SSR: 회귀의 편차제곱의 합 (Sum of Squares for Regression).
- SSE: 잔차의 편차제곱의 합 (Sum of Squares for Error).
4. SSX와 기본 통계 변수들 간의 관계
1. SSX와 평균:
- SSX는 변수 X의 각 데이터 값이 평균 $ \mu \ $ 에서 얼마나 떨어져 있는지를 제곱한 값의 합입니다. 즉, 편차를 제곱하고 모두 더한 것이 SSX입니다.
\[
SSX = \sum_{i=1}^{n} (x_i - \bar{x})^2
\]
여기서 \(x_i\)는 각 데이터 값, \(\bar{x}\)는 데이터의 평균입니다.
2. SSX와 분산:
- 분산(Variance)은 SSX를 데이터 개수 \(n\)로 나눈 값입니다.
\[
\text{분산} (\sigma^2) = \frac{SSX}{n}
\]
분산은 데이터 값들이 평균에서 얼마나 퍼져 있는지를 나타내는 지표로, SSX를 표본 크기 \(n\)으로 나누어 계산합니다.
만약 표본 분산(sample variance)을 구하려면 \(n\) 대신 \(n - 1\)을 사용합니다.
\[
\text{표본 분산} (s^2) = \frac{SSX}{n - 1}
\]
3. SSX와 표준편차:
- 표준편차(Standard Deviation)는 분산의 제곱근입니다. 따라서, SSX를 이용해 분산을 구한 후, 표준편차를 구할 수 있습니다.
\[
\text{표준편차} (\sigma) = \sqrt{\frac{SSX}{n}}
\]
표본 표준편차(sample standard deviation)의 경우도 마찬가지로 표본 분산의 제곱근을 구합니다.
\[
\text{표본 표준편차} (s) = \sqrt{\frac{SSX}{n - 1}}
\]
요약
SSX는 기본 통계 변수들과 다음과 같은 관계를 가집니다:
- SSX는 평균에서 각 데이터 값들의 편차제곱을 모두 더한 값입니다.
- 분산은 SSX를 데이터의 개수로 나눈 값이며, 데이터 값들의 변동성을 나타냅니다.
- 표준편차는 SSX를 기반으로 구한 분산의 제곱근으로, 데이터가 평균에서 얼마나 퍼져 있는지 보여줍니다.
예시
- 데이터: \( [2, 4, 6, 8] \)
- 평균: \( \bar{x} = 5 \)
- SSX:
\[
SSX = (2-5)^2 + (4-5)^2 + (6-5)^2 + (8-5)^2 = 9 + 1 + 1 + 9 = 20
\]
- 분산: \( \sigma^2 = \frac{SSX}{n} = \frac{20}{4} = 5 \)
- 표준편차: \( \sigma = \sqrt{5} \approx 2.236 \)


 : 1-VAR
: 1-VAR








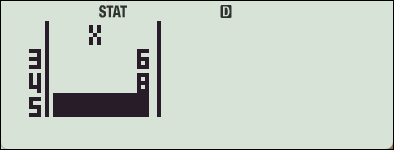



 : Var
: Var
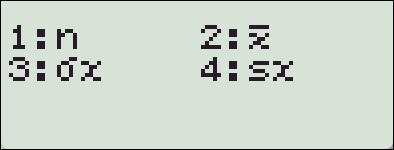
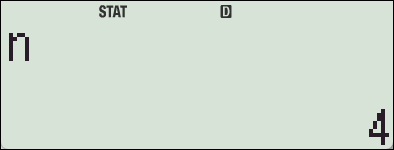
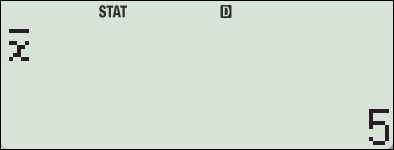
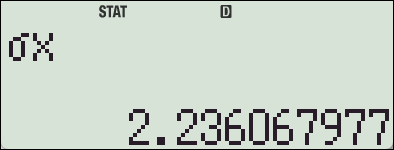

4. fx-570 ES 기종에서의 SSX, SSY
카시오 fx-570ES Plus 계산기에는 편차제곱의 합 (SSX, Sum of Squared Deviations)을 직접 구해주는 함수나 변수가 내장되어 있지 않습니다.
https://allcalc.org/5615 - [fx-570][fx-350] STAT 통계 모드 진행 과정 (변수 분석, 회귀 분석 등 전반)
일반적으로 통계 계산을 위해 제공되는 주요 기능들은 평균, 분산, 표준편차 등을 계산하는 것이기 때문에,
표준편차의 계산을 위한 중간 과정인 '분산'이나 '편차제곱의 합'은 통계 변수로 따로 저장되지 않았습니다.
(어떤 변수를 저장할지의 결정은 계산기 모델마다 다를 수 있습니다)
따라서 위에서 일일이 따로 계산하거나, 위의 공식(2. 분산) 을 반대로 계산하여 이미 계산되어 저장된 통계변수를 활용하여 값을 구할 수 있습니다.
\[
\text{편차제곱의 합}, SSX = \sigma^2 \cdot n = s^2 \cdot \left(n - 1\right)
\]










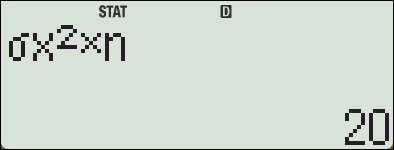
댓글1
-
세상의모든계산기
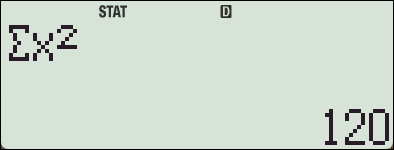
편차제곱의 합 SS 와
Sum 목록에 있는 x^2의 합은 서로 다른 값입니다.


 : Sum
: Sum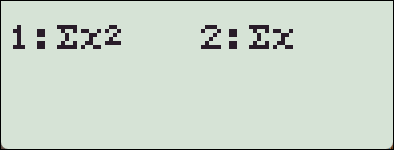



세상의모든계산기 님의 최근 댓글
ES 나 EX 와 비교해 'CW 입력 방식이 변화가 큰 편'이어서 지금까지 추천하지는 않았는데, - EX 모델이 완전 단종 & 그로 인해 짝퉁문제가 앞으로 더 심각해질 듯 보임 - 그렇다고 지금 ES 추천하기는 강호의 도리상 고개가 저어지고... 이제 모두 CW로 넘어갈 타이밍이 되지 않았나 싶네요. 그런데 왜 또 4자리로 나와서... ㅋㅋ 미치겠네 2025 12.28 버튼 갯수와 배치로는 의미있게 변한 것이 없습니다. 2025 12.28 fx-570 CW 는 정밀도가 올라갔음. 여기까지 매우 정밀한 값 = 1.7887597505251 Math ERROR 는 아니고 Time Out 이 발생함. 아쉽게도... 2025 12.28 에러는 피했지만 오차는 피할 수 없음. 매우 정밀한 값 = 1.7887597505251 fx-570 ES 나 EX 는 여기까지가 한계 더 이상 작은 값이 대입되면 실질적으로 분모가 0으로 처리되어 ERROR (수식마다 한계가 다름) 2025 12.28 진짜 색약 안경은 비싸서 살 생각은 없고, 알리에서 싸구려 구매해서 테스트 해 봤습니다. 프로그램과 비슷한 효과가 있고, (프로그램과 비교해서) 알리 싸구려 렌즈가 - 숫자 구분이 아주 약간 더 잘 되고 - 붉은 색상이 더 밝습니다. 채도가 높다고 해야하는 것 같네요. 주의할 점은 알리 색약 안경은 일상용으로는 절대 사용 불가입니다. - 내부 빛반사 방지 코팅이 없어서 내 눈알이 렌즈에 비치고, 그래서 실제로 보여야 할 것과 섞여 보입니다. - 필터 코팅도 최악이라서 중심부(=마젠타) 주변부(=노랑)으로 서로 다르게 색이 들어옵니다. 전반적으로 그라데이션 발생. - 외부에서 봤을 때 렌즈색이 튀기 때문에, 티가 많이 납니다. - 색 구분 면에서는 도움이 될 수도 있지만, 녹색(특정 파장)이 차단되어 LED 신호등의 녹색이 잘 안보일 수 있습니다. 2025 12.24