- TI nspire
[TI-nspire] 통계 - normCdf 누적분포함수, 정규분포 문제 풀이, feat. binomcdf
-
- 2025.06.04 - 06:18 2015.10.13 - 15:56 3145 3
1. 정규분포
normCdf(lowBound,upBound[,μ[,σ]]) ⇒
number if lowBound and upBound are numbers, list if lowBound and upBound are lists
Computes the normal distribution probability between lowBound and upBound for the specified μ (default=0) and σ (default=1).
For P(X ≤ upBound), set lowBound = -9E999.
문제 출처 : http://math7.tistory.com/49
1. 평균 800, 표준편차 40 정규분포 
x≤750 일 확률?
normCdf(−∞,750,800,40)
= normCdf(−∞,−1.25,0,1) = normCdf(−∞,−1.25)
= 0.10564983896266
2. 평균 11, 분산 16 정규분포 20 ≤ x 일 확률?
normCdf(20,∞,11,√(16))
= normCdf(2.25,∞,0,1) = normCdf(2.25,∞)
= 0.012224433401682
3. 평균 70, 표준편차 8 정규분포 80 ≤ x ≤ 90 학생의 비율?
normCdf(80,90,70,8)
= normCdf(1.25,2.5,0,1) = normCdf(1.25,2.5)
= 0.099440159109161
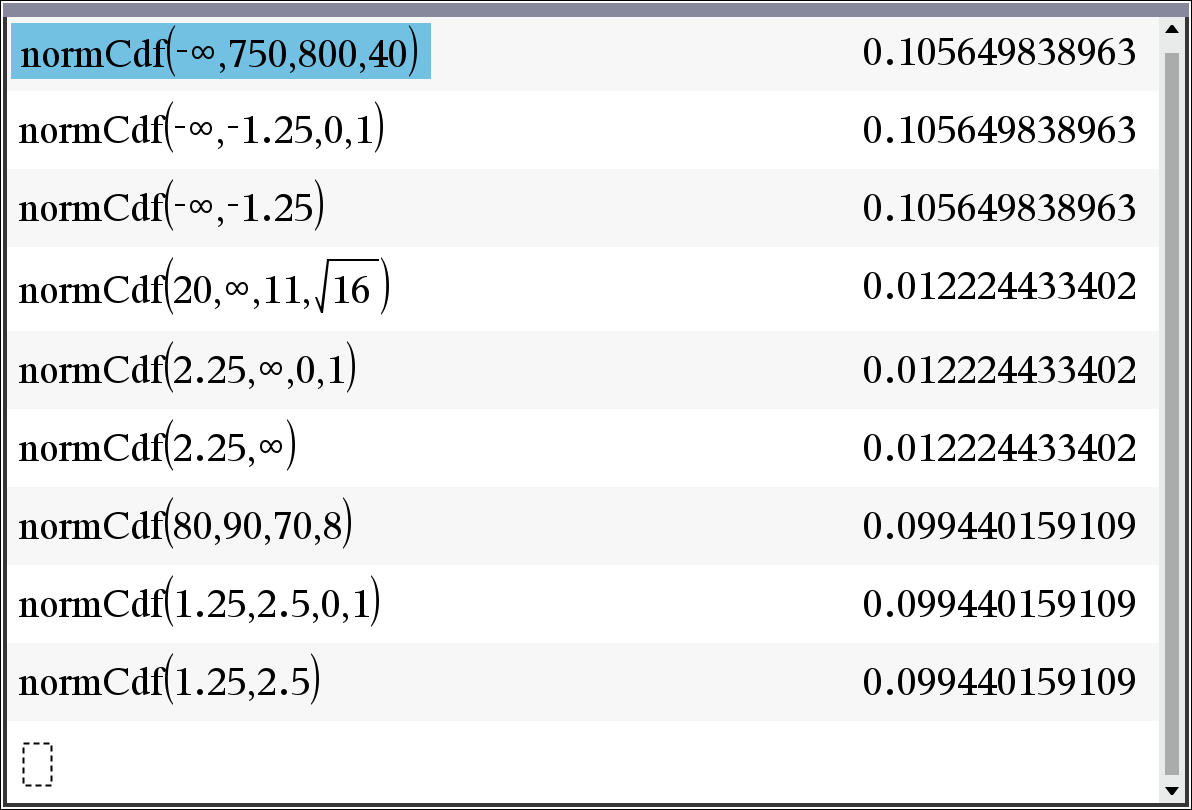
※ 표준화 하지 않아도, 계산기로 즉시 결과를 구할 수 있다.
표준화하는 이유는 표준화되지 않은 확률밀도함수를 매번 적분하기가 까다로워서인데, 계산기는 매번 적분하는데 큰 무리가 없기 때문에 굳이 표준화하는 수고를 거칠 필요가 없음. (맞나?)
2. 이항분포 vs 정규분포
문제 출처 : http://suhak.tistory.com/110
1. 검은 공 1 + 흰 공 3 인 주머니에서 공을 꺼내보고 다시 넣는다. 192회 시행시 검은 공이 48번 이상 60번 이하 나올 확률은?
└ 
정규분포와 이항분포는 가까울 뿐, 똑같지는 않다!
2. 주사위 450회 던질 때 3의 배수가 나온 횟수가 130회 이상 170회 이하일 확률?
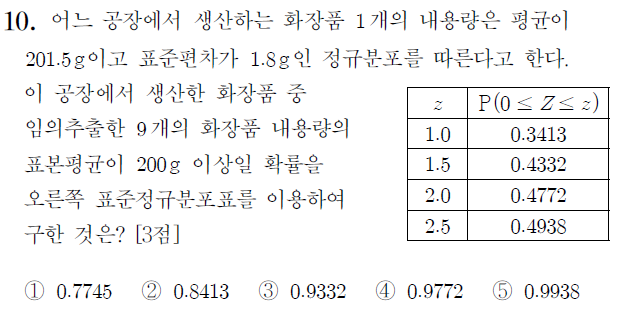
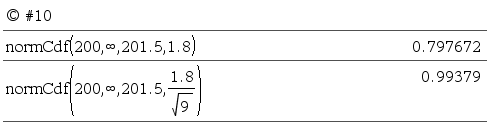
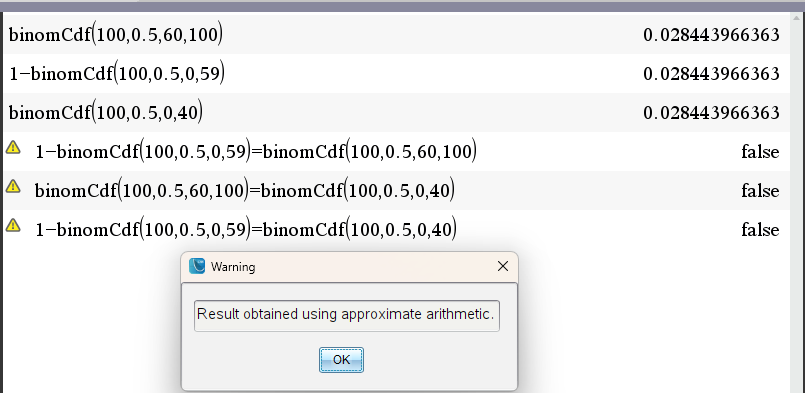
3. 주의
normCDF() 계산 결과값에 오차가 조금 있는 듯 합니다.
-
25
세상의모든계산기 님의 최근 댓글
적용사례 4 - 파장 스펙트럼 https://news.samsungdisplay.com/26683 ㄴ (좌) 연속되는 그라데이션 ➡️ (우) 540 이하 | 구분되는 층(색) | 560 이상 - 겹치는 부분, 즉 540~560 nm 에서 색상이 차단? 변형? 된 것을 확인할 수 있음. 그럼 폰에서 Color Vision Helper 앱으로 보면? ㄴ 540~560 nm 대역이 검은 띠로 표시됨. 완전 차단됨을 의미 2025 11.05 빨간 셀로판지로도 이시하라 테스트 같은 숫자 구분에서는 유사한 효과를 낼 수 있다고 합니다. 색상이 다양하다면 빨강이나, 노랑, 주황 등도 테스트해보면 재밌겠네요. 2025 11.05 안드로이드 앱 - "Color Vision Helper" 다운받아 본문 내용을 카메라로 찍어 보니, 본문 프로그램에서는 애매하게 보이던 부분에서도 구분이 완전 확실하게 되네요. 숫자 구분 능력 & 편의성 면에서 압도적이라고 할 수 있겠습니다. 2025 11.05 적용 사례 3 - 색상표 https://namu.wiki/w/%ED%97%A5%EC%8A%A4%20%EC%BD%94%EB%93%9C 적녹 색약 기준에서 필터 후 색깔을 느낌으로 표현하면 녹색 계열이 좀 차분? 묵직? 해지는 느낌 적색 계열이 전반적으로 조화를 이루지 못하고 튀는? 느낌 노랑이가 사라지는 느낌. * 적색 계열에서 글씨가 살짝 안보이는 것은 계조 문제(프로그램 문제)일 수 있겠다는 생각 2025 11.04 적용 사례 2 - 셔터스톡 https://www.shutterstock.com/ko/search/%EC%83%89%EC%95%BD%EA%B2%80%EC%82%AC?image_type=illustration 2025 11.04