- TI nspire
[TI-Nspire] 기본 기능을 이용한 라플라스 변환
한국어로 번역한 문서 https://allcalc.org/50260 를 TI-Nspire 용으로 추가 가공한 문서입니다.

소개
TI 계산기에는 라플라스 변환과 역변환을 계산하기 위한 미리 프로그래밍된 함수가 없습니다.
하지만 여러 웹사이트에서 이를 제공합니다 :
역자 주) TI-nspire 용으로 컨버팅 해당 문서는 https://allcalc.org/5003 입니다.
여기서 우리가 제안하는 것은, "TI의 기본 함수만을 사용하여도 충분히 잘 해낼 수 있다는 것을 보여주는 것"입니다.
라플라스 변환
먼저 라플라스 변환은 매개변수 s의 특정 값에 대해 수렴하는 이상적분임을 주목해야 합니다:
$ f\left( t\right) \leftrightarrow F\left( s\right) \equiv \int _{0}^{\infty }f\left( t\right) \cdot e^{-s\cdot t}dt $
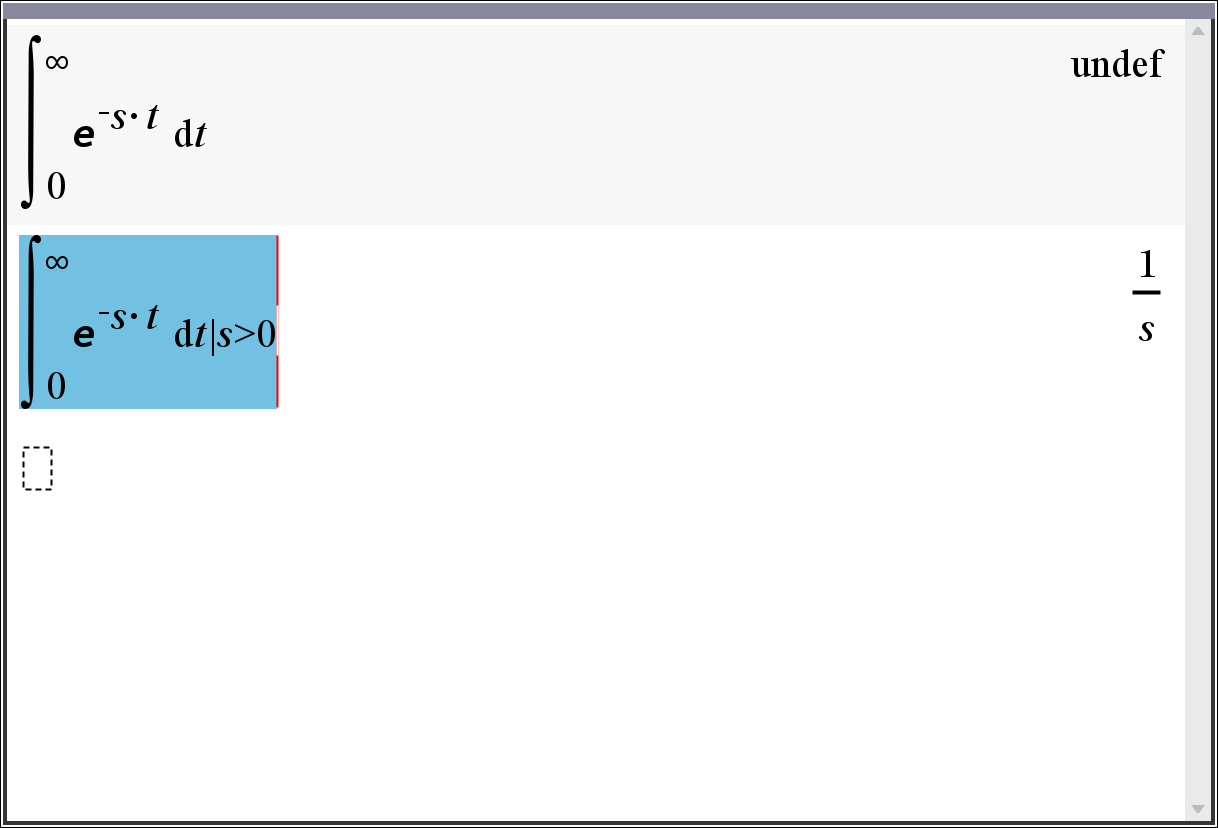
TI는 s에 대한 도메인이 지정되지 않으면 정의할 수 없습니다. (그림 1).∫(e^(−s*t),t,0,∞)|s>0
라플라스 변환을 함수로 정의할 수 있습니다.

하지만 TI-89와 달리 제약연산자(|) 를 한꺼번에 넣어서 정의하면 조각함수(piecewise function) 로 바뀌면서 오류가 발생합니다.
따라서 TI-nspire에서는 제약연산자 부분을 함수정의와 분리하고, 다시 함수와 결합해 사용해야 하는 불편함이 있습니다.
TI-89 에서는 위의 la(f,t,s) 함수의 수렴이 느려서 Lim 함수를 결합한 lala(f,t,s) 함수라는 대안을 찾았지만,
TI-nspire 에서는 속도가 충분히 빨라졌기 때문에 속도 때문에 대안을 찾을 필요는 없고,
다만 TI-89 에서 찾은 대안을 Nspire에서 사용하면 제약 연산자를 재결합해서 사용하지 않아도 되기 때문에
TI-nspire 에서도 유용한 대안이 됩니다.
* 여기서는 lala(f,t,s) 대신 lapl(f,t,s) 라는 함수명을 사용하겠습니다.

ㄴ lapl(f,t,s) := −lim(∫(f*e^(−s*t),t),t,0,1)
무한대에서의 값이 0이 됨을 이용하여 부적절한 적분(undef)을 피할 수 있습니다.
실제로, 라플라스 변환을 계산하는 함수들은 지수 차수입니다. 이는 s를 충분히 크게 선택하면
$ \lim _{t\rightarrow \infty }f\left( t\right) \cdot e^{-s\cdot t}=0 $ 을 얻게 된다는 것을 의미합니다.
부정적분 을 계산한 후에는 (f가 모든 곳에서 연속이고 TI가 적분 상수를 추가하지 않는다고 가정하면)
$ \int f\left( t\right) \cdot e^{-st}dt $ 라고 하면 됩니다.
극한은 t = 0에서의 평가가 0의 오른쪽에서 계산되어야 한다는 사실에서 비롯됩니다.
이제 훨씬 더 심각한 문제인 역변환을 다루겠습니다.
역 라플라스 변환
$ F\left( s\right) =\dfrac{1}{\left( s-2\right) ^{2}\cdot \left( s^{2}+6s+13\right) } $
의 역변환 계산을 고려해 봅시다.
여기서는 제곱 완성을 수행해야 합니다: 부분 분수 전개 전에 이를 수행하는 것이 좋습니다(그림 3).

변환 표에서 다음과 같은 대응관계를 알아야 합니다:
$ \dfrac{s+a}{\left( s+a\right) ^{2}+b^{2}}\leftrightarrow e^{-at}\cos bt,\dfrac{b}{\left( s+a\right) ^{2}+b^{2}}\leftrightarrow e^{-at}\sin bt $
$ \dfrac{1}{s+a}\leftrightarrow e^{-at}\text{ and }\dfrac{1}{\left( s+a\right) ^{2}}\leftrightarrow t\cdot e^{-at} $
따라서 답은
$ f\left( t\right) =\dfrac{10e^{-3t}\cos 2t}{841}+\dfrac{21e^{-3t}\sin 2t}{1682}-\dfrac{10e^{2t}}{841} +\dfrac{t \cdot e^{2t}}{29} $
입니다.
컨볼루션으로도 진행할 수 있습니다:
컨볼루션 속성에 따르면 F(s) = X(s) H(s)인 경우,
$ \text{with } F\left( s\right) \leftrightarrow f\left( t\right), X\left( s\right) \leftrightarrow x\left( t\right) \text{ and } H\left( s\right) \leftrightarrow h\left( t\right), $
$ \text{then } f\left( t\right) = x\left( t\right) \ast h\left( t\right) \equiv \int _{0}^{t}x\left( \tau \right) h\left( t-\tau \right) d\tau $
입니다.
여기서 우리는 다음 식을 얻습니다. :
$ F\left( s\right) =\dfrac{1}{\left( s-2\right) ^{2}\cdot \left( s^{2}+6s+13\right) } $
$ =\left( \dfrac{1}{\left( s-2\right) ^{2}}\right) \left( \dfrac{1}{\left( s+3\right) ^{2}+4}\right) \leftrightarrow t\cdot e^{2t}\ast \dfrac{1}{2}e^{-3t}\sin 2t $
그리고 TI는 컨볼루션 적분을 처리합니다(그림 4 a 참조).
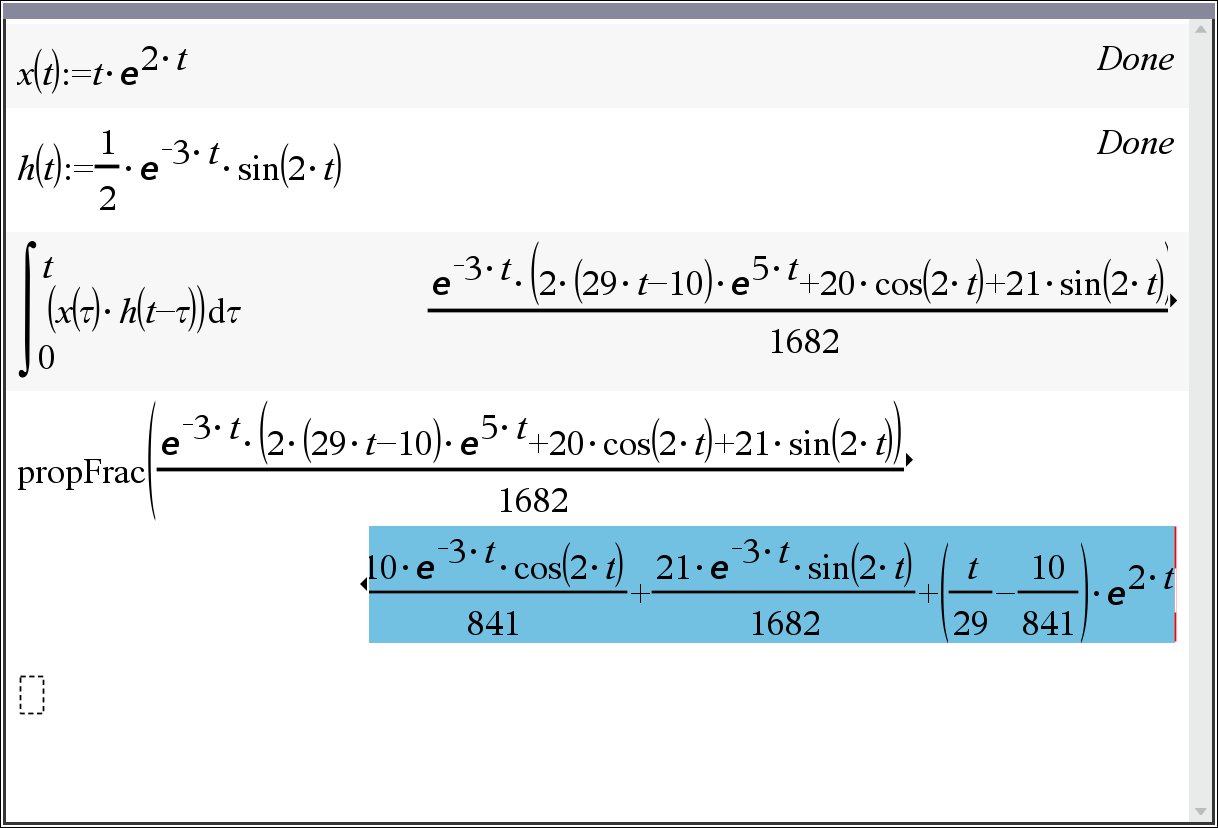
그림 4 b와 4 c는 결과의 단순화를 보여줍니다.
복소수를 사용하여 부분 분수로 전개할 수도 있습니다.
TI에서 선언되지 않은 변수는 실수로 간주되지만, 이 변수에 밑줄 "_" 기호를 추가하면 복소수로 간주됩니다.
실제로 s가 실수인지 복소수인지에 따라 TI가 $ \dfrac{1}{s+i} $ 를 어떻게 단순화하는지 보세요(그림 5).
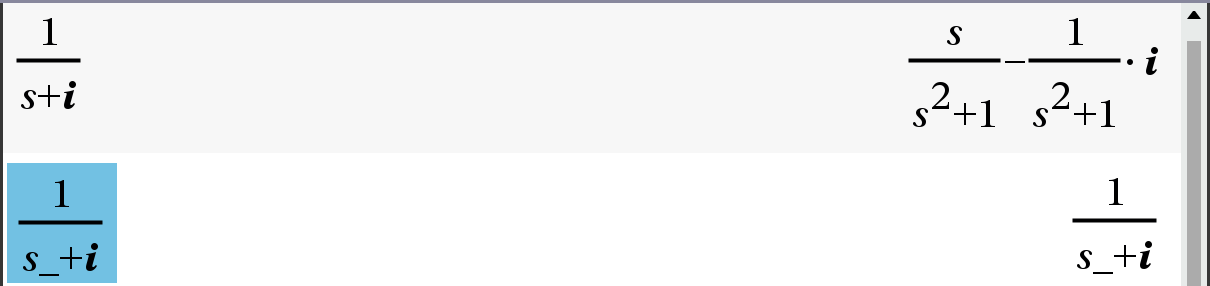
이 단계에서 대응관계 $ \dfrac{1}{s+a} \leftrightarrow e^{at} [ Re\left( s\right) > -a] $ 와
오일러 공식 $e^{it} =\cos(t) + i \sin(t) , \left( t\in R\right) $ 을 사용하면 복소 부분 분수가 수행된 후 역 라플라스 변환을 계산할 수 있습니다.
여기서 g(s)라고 부를 $ F\left( s\right) =\dfrac{1}{\left( s-2\right) ^{2}\cdot \left( s^{2}+6s+13\right) } $ 의 예를 다시 살펴봅시다.
부분 분수로 전개하기 전에 복소수로 인수분해하는 것이 중요합니다(그림 6 a);

이 작업은 s가 복소수라는 제약 하에 수행됩니다(그림 6 b 및 6 c).
그런 다음 복소 근이 켤레 쌍으로 나타난다는 사실을 이용하여
$ ze^{\left( 3+2i\right) t}+\overline{z}e^{\left( 3-2i\right) t}-\dfrac{10}{841}e^{2t}+\dfrac{1}{29}te^{2t}$ 라고 쓰면 됩니다.
여기서 z는 숫자 $ z = \dfrac{5}{841} + \dfrac{21}{3364}i $ 로 정의되었습니다.
TI는 "conj"를 사용하여 복소수를 켤레복소수로 만듭니다(그림 7).

미분방정식 시스템과 라플라스 변환
TI는 라플라스 변환을 사용하여 미분방정식 시스템을 해결하는 데 매우 유용할 수 있습니다.
계산기가 길고 지루한 계산을 처리하므로 사용자는 해결할 방정식만 지정하면 됩니다.
다음 시스템을 고려해 봅시다:
$ \begin{cases}\dfrac{dx}{dt}-3x-6y=27t^{2},,x\left( 0\right) =5\\ \dfrac{dx}{dt}+\dfrac{dy}{dt}-3y=5e^{t},y\left( 0\right) =-1\end{cases} $
s 도메인으로 변환하면 다음을 얻습니다:
$ \begin{cases}sX-5-3X-6Y=\dfrac{54}{s^{3}}\\ sX-5+sY+1-3Y=\dfrac{5}{s-1}\end{cases} $
여기서 X와 Y는 각각 x와 y의 라플라스 변환을 나타냅니다. 마지막으로, 우리 시스템을 행렬 형태로 다시 쓰면 다음을 해결해야 합니다:
$ \begin{bmatrix} s-3 & -6 \\ s & s-3 \end{bmatrix}\begin{bmatrix} X \\ Y \end{bmatrix}=\begin{bmatrix} \dfrac{54}{s^{3}}+5 \\ \dfrac{5}{s-1}+4 \end{bmatrix} $
TI가 개입하고 우리는 행렬을 정의합니다(그림 8).

계수 행렬을 m이라고 부르고 오른쪽 행렬을 b라고 부르기로 합니다.
좋은 옛날 크라머 방법은 이제 쓸모없어졌습니다!
실제로 TI의 "simult" 함수를 사용하면 정사각형 선형 시스템을 해결할 수 있습니다(그림 9).
지루한 행렬식의 몫을 계산할 필요가 없습니다(또는 를 입력해도 결과는 같았을 것입니다).
이제 부분 분수로 전개하기만 하면 됩니다.
"expand" 명령은 리스트와 행렬에서도 작동합니다. "expand"의 구문은 expand(exp [, var])입니다. (그림 10).
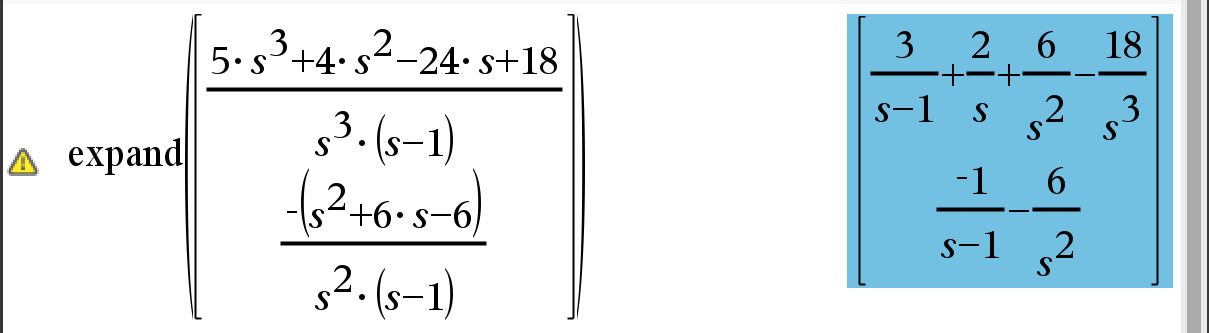
라플라스 변환 표를 사용하여 다음과 같이 쓸 수 있습니다:
$ x\left( t\right) =3e^{t}+2+6t-9t^{2} $
$ y\left( t\right) =-e^{t}-6t $


세상의모든계산기 님의 최근 댓글
감사합니다. 주말 잘 보내세요. 2026 03.06 [fx-570 ES] 과학 상수를 이용한 계산에서 에러 발생 상황 https://kin.naver.com/qna/detail.naver?d1id=11&dirId=1118&docId=492235162&page=1&answerNo=1 vs 2026 03.01 과학상수를 이용한 계산 중 자릿수 한계로 인한 에러 발생 가능성 https://allcalc.org:443/board_calculators/6925#comment_57029 2026 03.01 기본 어댑터 MODEL : AD0301-1202500GB INPUT : 100~240V, 50~60Hz, 0.8A Max OUTPUT : 12.0V, 2.5A, 30.0W ㄴ 측정시 플러그 외경/내경 : 5.5mm / 2mm 2026 02.15 엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10