- TI nspire
[TI-nspire] 계산 모드 : 근사값 vs 참값 Calculation Mode : Approx vs Exact
-
- 2025.05.23 - 07:17 2015.04.16 - 09:00 5061 4
[TI-nspire] 에서는 결과를 정확하게 계산하여 보여주기도 하고, 대충 근사값으로 계산해서 그 값을 보여주기도 합니다. 보통의 경우라면 정확한 값을 나타내주는 Exact 모드가 좋습니다만, 때에 따라서는 Approx 모드가 편리할 때도 있습니다.
참 값 예) √2, sin-1(1/3)
1. 설정으로 변경 (지속 적용)
Document Setting 화면에 가서 Calculation Mode 를 바꿔 주시면 됩니다.
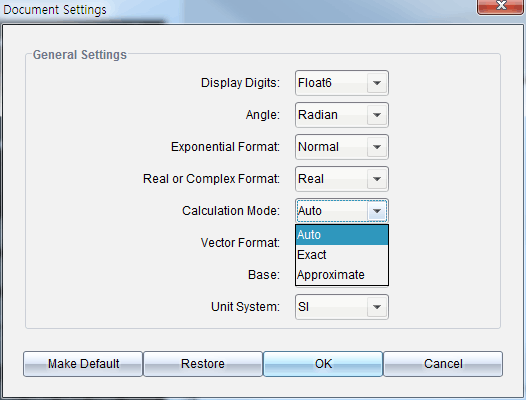
* CAS 모델에는 "Exact" 모드까지 총 3가지 선택지가 있고,
nonCAS 모델에는 (Auto/Approximate) 2가지 선택만 가능합니다.
2. 계산시 적용 (1회성)
엔터 위의 ≒(물결표시) 를 실행하기 위해 
(컨트롤 엔터) 를 누르세요.
설정과 무관하게 강제로 근사값 결과를 출력합니다. 1회만 적용되며, 그 다음부터는 원래 설정대로 적용됩니다.
3. 함수로 적용 (1회성)
approx(Expr)
exact(Expr,[Tolerance])
식(Expr) 전체를 위 함수들로 묶어주는 방법입니다.
4. 주의
수식에 소숫점이 들어가면 강제로 근사(Approx) 모드로 계산됩니다.
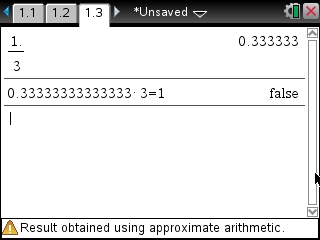
근사값 결과(Ans)를 이용하다 보면 오차에 따른 오류가 발생할 수 있으니 주의하시기 바랍니다.
(Result obtained using approximate arithmetic)
-
25
댓글4
-
세상의모든계산기
[TI-89 Titanium]에서도 nspire와 동일한 내용이 적용됩니다.
- 설정으로 변경
[MODE] [F2]
[Exact/Approx] [▶] [3:Approximate]
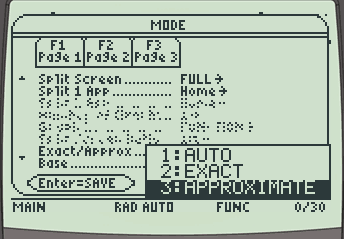
- 1회용으로 사용
- 설정으로 변경
-
세상의모든계산기
The non-CAS version will keep "exact" values that can be expressed in rational form.
The CAS version will keep "exact" values that can be expressed in both rational and irrational forms.AUTO on non-CAS version
AUTO on CAS version
출처 : https://mathbits.com/MathBits/TINSection/General/Mode.html
세상의모든계산기 님의 최근 댓글
2번 사진 3개 사진 공통적으로 구석(corner) 에 증상이 있다는 특징이 있네요. 영상 찾아보니 이 가능성이 가장 높은 듯 합니다. https://www.youtube.com/watch?v=zxRBohepzwc ㄴ Liquid Crystal Leakage (액정 누설). ㄴ 손으로 밀어내니 주변으로 밀려나네요. 그래서 점으로 보이기도 하구요. 2025 10.29 500! 의 십진수 근사값 확인 500! = 1.22013682599111006870123878542304692625357434280319284219241358838 × 10^(1134) (참값, 울프람 알파) 2025 10.29 관련 라이브러리 https://allcalc.org/56263 sgn(x) 내장된 부호 함수(signum function)와 달리, 이 함수의 sgn(0)은 0을 반환합니다. 2025 10.29 라이브러리로 사용할 수 있습니다. (제작자 추천) 1. mylib 폴더에 넣기 2. Actions ➡️ library ➡️ refresh libraries 실행 하기 2025 10.29 ChatGPT-5 기호(÷, /, :) 자체는 의미적으로 같은 “나눗셈”을 뜻하지만, 문맥(사람이 쓰는 수학 vs 컴퓨터/프로그래밍)에 따라 해석 우선순위가 달라질 수 있습니다. 🔹 1️⃣ 전통 수학 표기 — ÷, /, : 수학 교과서, 논문, 일반 문서 등에서는 셋 다 의미적으로 “나누기”로 간주됩니다. 즉, 48÷2(9+3), 48/2(9+3), 48:2(9+3) 은 같은 의미로 받아들여야 합니다. 모두 사람의 수학 관행적 해석이 적용되어 48 ÷ 2 × (9+3) = 288 로 처리되죠. 즉, 기호가 바뀌어도 결과는 바뀌지 않습니다. 🔹 2️⃣ 컴퓨터·프로그래밍 문맥에서 / 사용 시 컴퓨터는 “생략된 곱셈(implicit multiplication)”을 따로 구분하지 못합니다. 따라서 다음 두 식은 완전히 다르게 인식됩니다. 표현 파이썬 등에서 해석 결과 48 / 2*(9+3) ((48 / 2) * (9+3)) 288 48 / 2(9+3) ❌ 문법 오류 (생략된 곱셈 인식 불가) — 즉, 컴퓨터 언어에서는 생략된 곱셈이 허용되지 않기 때문에, /는 반드시 명시적 *와 함께 써야 합니다. 🔹 3️⃣ “:” 기호의 경우 현대 수학에서는 “비율”을 나타내는 기호로 쓰입니다. a:b = \frac{a}{b} 따라서 (27 : 3(1+2)3) 같은 표현은 모호하거나 비표준적으로 간주됩니다. 대부분의 경우 계산기로는 입력 자체가 불가능합니다. ✅ 정리 기호 의미 결과 변화 주로 쓰이는 문맥 ÷ 나누기 없음 초중등 수학, 일반 표기 / 나누기 없음 (단, 프로그래밍에서는 생략 곱 불허) 수학/컴퓨터 : 비율 (또는 나누기 의미로 혼용) 보통 계산식에서는 사용 안 함 비, 비율 표기 🔹 결론 48 ÷ 2(9+3), 48/2(9+3), 48:2(9+3) 는 “수학적 의미”로는 동일하게 81로 해석됩니다. 하지만 프로그래밍이나 수식 파서(context) 에서는 /만 유효하고, 생략된 곱은 허용되지 않으며, :는 아예 다른 의미(비율)로 인식됩니다. 2025 10.28