- TI nspire
[TI-nspire CAS] solve() : 솔브 함수 ; 방정식의 해를 구하는 기능
-
- 2025.10.22 - 02:07 2015.01.23 - 20:14 30824 22
1. 개요
solve() 함수는 방정식이나 부등식의 실수해(real solutions)를 추정하여 반환하는 함수입니다.
결과가 딱 떨어지는 일반 여타 함수들과는 달리 사용 방법이 조금 까다롭습니다.
└ 복소수 해를 구할 때에는 오직 csolve() 를 사용합니다.
└ [TI-nspire non-CAS] 기종은 nsolve() 또는 linsolve() 만을 이용할 수 있으므로 복소수 해를 구할 수 없습니다.
* solve() 함수는 ⓐ 가급적 정확(exact)한 답을 찾으려고 하고, ⓑ (상황에 따라) 찾을 수 있는 최대한 많은 답을 표시하려고 합니다.
2. 사용 방법
2-1.
|
ⓐ solve(Equation, Var) ⇒ Boolean expression ⓑ solve(Equation, Var=Guess) ⇒ Boolean expression ⓒ solve(Inequality, Var) ⇒ Boolean expression |
'var' 만 넣어도 되고, 'var=guess' 로 결과 추정 값을 넣어도 됩니다. 일반적으로 아무 값이라도 추정값을 넣는 것이 더 바람직합니다. guess 값에 따라 반환되는 결과값이 달라질 수도 있습니다.
2-2.
|
ⓐ solve(Eqn1 and Eqn2[and …], VarOrGuess1, VarOrGuess2[, …]) ⇒ Boolean expression ⓑ solve(SystemOfEqns, VarOrGuess1, VarOrGuess2 [, …]) ⇒ Boolean expression ⓒ solve({Eqn1, Eqn2 [,...]} {VarOrGuess1,VarOrGuess2 [, … ]}) ⇒ Boolean expression |
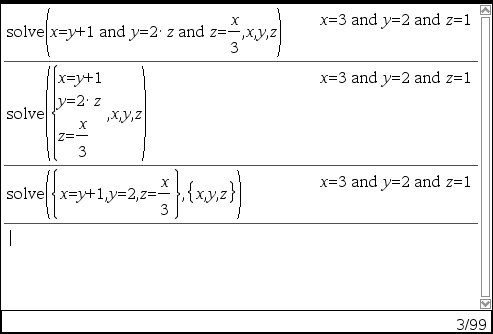
ㄴ 여기서의 결과는 같지만, 다중변수 var 지정방법에 따라 결과의 표시방법 및 순서는 달라질 수도 있습니다.
* solve() 의 결과는 항상 Boolean expression 임을 주목하세요.
[아래 출처 : https://bard.google.com/]
Boolean expression은 참과 거짓을 나타내는 표현입니다. Boolean expression은 논리 연산자를 사용하여 두 개 이상의 Boolean value를 결합하여 Boolean value를 생성할 수 있습니다.
Boolean expression의 가장 일반적인 논리 연산자는 AND, OR, NOT입니다. AND 연산자는 두 개의 Boolean value가 모두 참일 때 참을 반환하고, OR 연산자는 두 개의 Boolean value 중 하나라도 참일 때 참을 반환합니다. NOT 연산자는 Boolean value가 거짓일 때 참을 반환하고, 참일 때 거짓을 반환합니다.
예를 들어, "a > 0 AND b < 10"은 a가 0보다 크고 b가 10보다 작은지 여부를 나타내는 Boolean expression입니다. 이 표현의 결과는 a와 b의 값에 따라 참 또는 거짓이 될 수 있습니다.
Boolean expression은 프로그래밍 언어에서 조건문, 반복문, 함수의 인자 등으로 사용됩니다. 조건문은 Boolean expression의 결과에 따라 코드를 실행하거나 실행하지 않도록 제어하는 데 사용됩니다. 반복문은 Boolean expression의 결과가 참인 동안 코드를 계속 실행하도록 제어하는 데 사용됩니다. 함수의 인자로 Boolean expression을 사용하면 함수가 실행될 때의 조건을 제어할 수 있습니다.
꿀팁
solve() 에서 사용하는 변수가 여러개인 경우, 결과가 x=ㅁㅁ and y=ㅇㅇ or x=◇◇ and y=△△ 의 꼴(=boolean expression)로 나오게 되므로 결과 그대로를 다른 수식에 이용하는 것은 어렵습니다.
이 때 exp▶list(expr, {x,y,z}) 함수를 이용하면 결과를 행렬 형태로 변경시킬 수 있습니다.
[프로그램] "or" 단위로 구분된 수식을 "리스트 / 매트릭스" 형태로 바꿈
https://allcalc.org/41844
ㄴ or 단위만 없애려면 위 프로그램을 사용하실 수도 있습니다.
3. 
주의 사항
- 문제 발생 유형
답이 나오지 않는 경우 = false
입력한 식이 그대로 나온 경우
답이 표시됐으나 원하는 답이 아닌 경우
답이 표시되지 않고 모래시계만 계속 돌아가는 경우
- 문제해결에 도움이 되는 방법들
【ctrl】【enter】 (근사값 모드)로 풀어보기
입력한 식의 재확인(특히 문자*(괄호)에서 곱하기 생략한거 없는지 확인, 함수형식 맞는지)
추정값(Guess) 입력하여 재계산 (매우 중요)
solve(~~~) | a<x<b 꼴로 범위 지정하여 재계산
입력한 수식을 변형하여 재입력
그래도 안되면, 최종 단계로 그래프로 그려보고 확인
-
25
댓글22
-
세상의모든계산기
예시1) 버그 - 변수에 대한 큰 지수가 있을 때, 오류값 출력 (예 : 이자율)
solve 자체의 버그는 아니고, 계산기 고유의 버그
(※ 내부 유효숫자(internal significant digits) 문제로 발생함)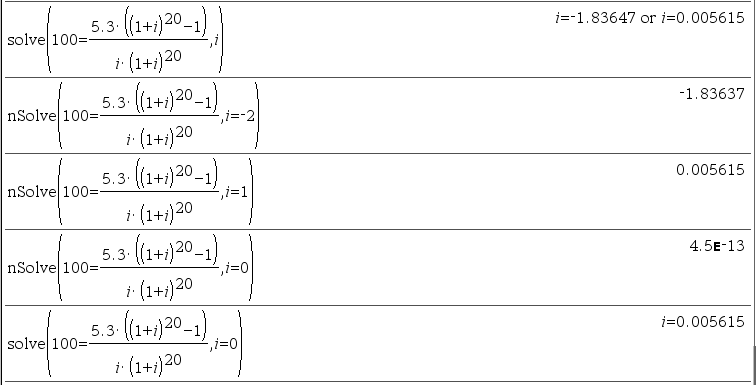
버그 내용 : 4.4999999999999E−13 는 해가 아님.
-
1
세상의모든계산기
유사 사례 - 이자율 계산
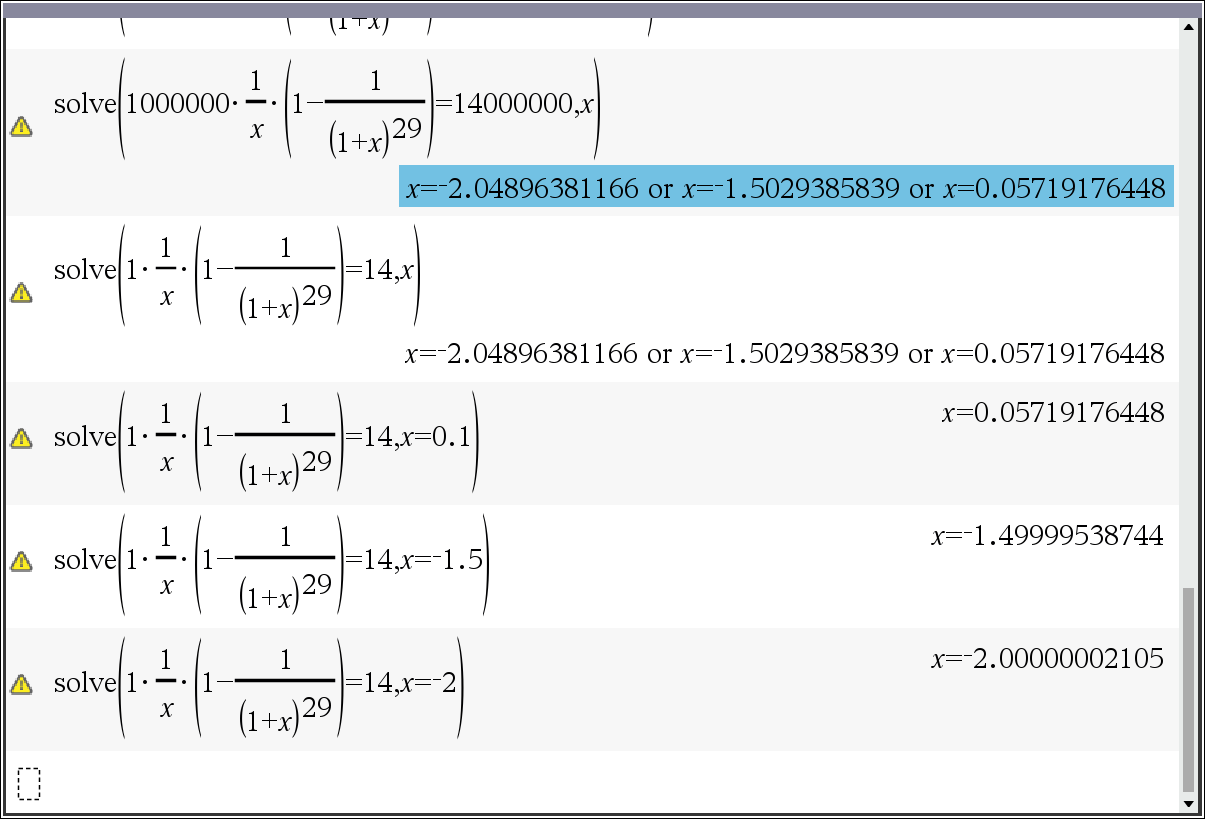
Questionable accuracy. : When applicable, try using graphical methods to verify the results.시도 1 : 초기값 지정 ⇒ 이자율에 해당할 수 있는 0.1(=10%) 로 지정하면 찾아짐
해결되지 않음 : 초기값 지정 ⇒ 음수 지정시 지정한대로 또 다른 오답이 찾아짐
시도 2 : nsolve(), ⇒ solve() 와 동일함.
최종 결론 : 위의 이자율 계산할 때는 |x>0 인 조건을 걸고, 정상 이자율(0 < r < 1) 을 초기값으로 넣는 것이 최선
-
세상의모든계산기
예시2) 식의 정리 방법. 여러 문자 중 특정 문자로 뽑아낼 때
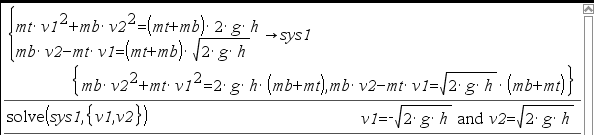
* 이런식으로 입력하더라도, 조건이 꼭 필요한 경우에는 뒤에 치렁치렁 다 데리고 나올 때 있음.
-
세상의모든계산기
예시3) 적분을 포함한 식의 solve : 가능
답이 맞는지는 모르겠음
-
세상의모든계산기
예시4) solve 결과 false 가 나올 때
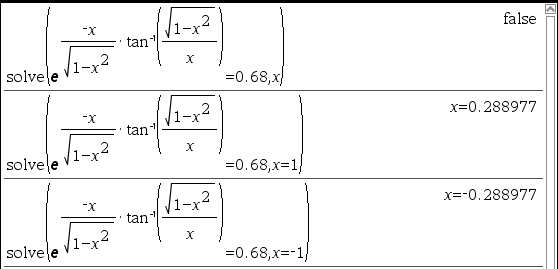
추정값(=Guess) 입력여부에 따라 결과값이 달라질 수 있습니다.
-
세상의모든계산기
예시5) 입력한 수식의 형태(좌변 vs 우변 위치) 에 따라 결과가 달라질 수도
-
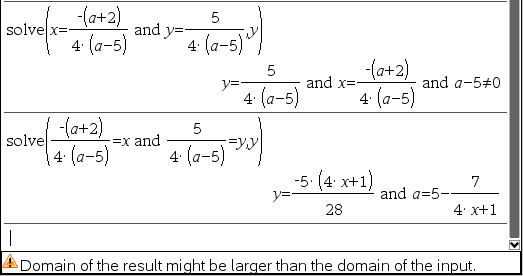
세상의모든계산기
예시6) 버그 - Solve 자체의 버그인데 계산기 OS 에 따라 다르게 발생함
V 4.0 에서는 Doc-Setup-Real or Complex Format 설정에 따라 복소수 결과가 나올 수도 있음. 게다가 오답
V 3.2 에서는 설정과 관계없이 실수결과값이 구해짐. 정상위 문제를 csolve 로 풀었을 때는
V 4.0 에서는 무한루프(시계) 상태가 되고,
V 3.2 에서는 주기함수 형태로 답이 나옵니다.
-
[질문] exp▶list(expr, {x,y,z})
solve() 에서 사용하는 변수가 여러개인 경우, 결과가 x=ㅁㅁ and y=ㅇㅇ or x=◇◇ and y=△△ 의 꼴로 나오게 되므로결과 그대로 다른 수식에 이용하는 것은 어렵습니다.
이 때 exp▶list(expr, {x,y,z}) 함수를 이용하면 결과를 행렬 [ㅁㅁ ㅇㅇ △△]형태로 변경시킬 수 있습니다.
이 부분
exp▶list(expr, {x,y,z}) 이 부분에 대해서 좀 자세히 알려주실 수 있나요?
함수로 만들어야 할 것 같은데, expr 부분을 어떻게 입력해야하는지 모르겠습니다.
x= 1 and y=4 and z=3 이런식으로 된 것을 인식하게 만드는 것 같은데
행렬1x3 (x,y,z)▶list(expr, {x,y,z}) 로 입력해도 안되서 이렇게 질문합니다. - 1
-
세상의모든계산기
예시 8) 버그
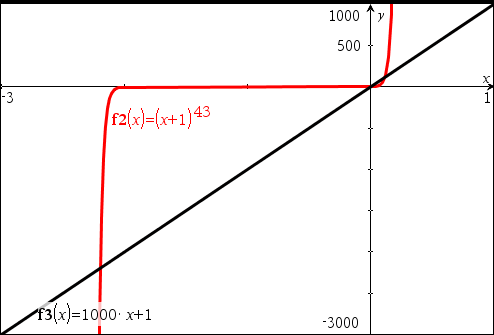
실수해가 분명 3개인 상황인데...
x=-2.67537 과 x=-0.68638 은 왜??? 찾아진건지 모르겠음.
http://www.wolframalpha.com/input/?i=(x%2B1)%5E43-1000*x-1
-
세상의모든계산기
비교) nsolve vs solve
ㄴ 여기서 false 의 원인은 "Overflow replaced by ∞ or -∞"간혹 solve 로는 안나오는 답이 nsolve로는 나오는 경우가 있습니다.
이 때는 【ctrl】【enter】 가 도움이 될 수 있습니다. -
세상의모든계산기
예시10) 답이 반복되는 삼각함수에서 특정한 해만 찾을 때
-> 범위를 지정(추천)하거나, 추정값을 입력하시면 됩니다.
-
세상의모든계산기
복잡하지 않은 경우에는 공역≠치역 일 때,
solve 로 범위나 구간을 포함한 정답이 찾아집니다.
-
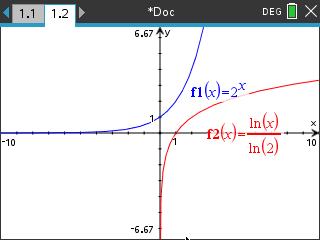
rPtkscal
[질문]
문자로 되어있는 식에서 원하는 문자들(분수)로 답을 정리하고 싶을 때 solve를 사용해서 표현할 수 있을까요?
https://allcalc.org/27981 이 글 처럼, 문자로 결과를 받으려고 합니다.a(b-c)=c/d+c/e 라는 식에서 c/b=dea/(ade+d+e) 이런 식으로 표현하고 싶은데, solve(a(b-c)=c/d+c/e, c/b)를 해보면 "Error: Argument must be a variable name."이라는 에러가 뜹니다. 혹시 어떻게 표현하면 구할 수 있을까요?
-
1
세상의모든계산기
[답변]
ⓐ solve(Equation, Var) ⇒ Boolean expression
c/b 는 Var 가 아니라 Expression 에 해당하기 때문에 에러가 나는 것입니다.
따라서 solve() 를 이용해서는 원하시는 답을 얻으실 수 없고,
제약식을 같이 섞어서 원하시는 답을 구하실 수 있습니다.[TI-nspire] 수식에 "|"(Constraint Operator) 조건식, 제약식을 붙이는 방법
ㄴ ▲ Warning : Domain of the result might be larger than the domain of the input.
-
2
세상의모든계산기
solve(abcde,{c,b}) 로 한번에 답을 구한 다음에
-> 통째로 집어넣어 답을 구하는 것이 가장 이상적입니다만,위에서는 그게 안되어서 solve() 를 두번 나누어 답을 구한 것입니다.
한꺼번에 넣었을 때 답이 안나오는 이유는,
s.bc 가 or 로 엮어진 3가지 경우의 답변을 포함하고 있기 때문입니다.▲ Warning : Constraint was ignored. Try evaluating a relation instead. For example, if
'Expr | (Condition_A or Condition_B)'
does not produce a desired result, try
'Var = Expr | (Condition_A or Condition_B)'3가지 경우를 각각 넣어보면 제각각 답이 나오기 때문에 답을 하나로 표시할 수 없는 것입니다.
앞선 답변에서처럼 s.b 와 s.c 를 각각 찾아서 답을 얻은 것에
느낌표(Warning) 경고가 나온 것도 경우에 따라 다른 답이 가능하기 때문에 발생한 거라고 보시면 되겠습니다.따라서 정확한 답은 아래에 3가지 경우를 모두 적으셔야 합니다.
-
1
세상의모든계산기
상수값을 a, b 에 지정하면,
문자변수 a, b 가 들어간 수식은 자동으로 a, b 가 숫자로 치환되어 사용됩니다.
따라서
solve 안에 숫자(상수)가 아닌 미지수 a, b 로 입력하려면 a, b 에 아무 값도 지정하지 말고 입력하시면 됩니다.
이미 지정되어 있다면 delvar 로 변수를 클리어(초기화)하고 사용하시구요.
[TI-nspire] 사용자 함수와 변수의 지정 (저장) 및 삭제 function and variables
https://allcalc.org/5752 -
세상의모든계산기
예시11) 선형 연립방정식에서 답이 false 로 나올 때
https://allcalc.org/55823
에러 메시지
세상의모든계산기 님의 최근 댓글
3×3 이상인 행렬의 행렬식 determinant https://allcalc.org/50536 2025 12.30 답에 이상한 숫자 14.2857142857가 들어간 것은 조건식에 소숫점(.) 이 들어가 있기 때문에 발생한 현상이구요. 100÷7 = 14.285714285714285714285714285714 소숫점 없이 분수로 식이 주어졌을 때와 결과적으로는 동일합니다. 2025 12.30 그럼 해가 무한히 많은지 아닌지 어떻게 아느냐? 고등학교 수학 교과과정에 나오는 행렬의 판별식(d, determinant)을 이용하면 알 수 있습니다. ㄴ 고교과정에서는 2x2 행렬만 다루던가요? 연립방정식의 계수들로 행렬을 만들고 그 행렬식(determinant)을 계산하여야 합니다. 행렬식이 d≠0 이면 유일한 해가 존재하고, d=0 이면 해가 없거나 무수히 많습니다. * 정상적인 경우 (`2y + 8z = 115`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 8 | 행렬식 값 = 1(0 - (-7)) - 1(8 - 0) = 7 - 8 = -1 (0이 아니므로 유일한 해 존재) * 문제가 된 경우 (`2y + 7z = 100`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 7 | 행렬식 값 = 1(0 - (-7)) - 1(7 - 0) = 7 - 7 = 0 (0이므로 유일한 해가 존재하지 않음) 2025 12.30 좀 더 수학적으로 말씀드리면 (AI Gemini 참고) 수학적 핵심 원리: 선형 독립성(Linear Independence) 3원 1차 연립방정식에서 미지수 x, y, z에 대한 단 하나의 해(a unique solution)가 존재하기 위한 필수 조건은 주어진 세 개의 방정식이 서로 선형 독립(linearly independent) 관계에 있어야 한다는 것입니다. * 선형 독립 (Linearly Independent): 어떤 방정식도 다른 방정식들의 조합(상수배를 더하거나 빼는 등)으로 만들어질 수 없는 상태입니다. 기하학적으로 이는 3개의 평면(각 방정식은 3D 공간의 평면을 나타냄)이 단 한 개의 점(해)에서 만나는 것을 의미합니다. * 선형 종속 (Linearly Dependent): 하나 이상의 방정식이 다른 방정식들의 조합으로 표현될 수 있는 상태입니다. 이 경우, 새로운 정보를 제공하지 못하는 '잉여' 방정식이 존재하는 것입니다. 기하학적으로 이는 3개의 평면이 하나의 선에서 만나거나(무수히 많은 해), 완전히 겹치거나, 혹은 평행하여 만나지 않는(해가 없음) 상태를 의미합니다. 질문자님의 사례는 '선형 종속'이 되어 무수히 많은 해가 발생하는 경우입니다. 2025 12.30 질문하신 연립 방정식은 미지수가 3개이고 모두 1차인 3원 1차 연립방정식입니다. 이상적으로 문제가 없다면 {x,y,z} 에 대한 좌표가 하나 나오게 됩니다. 원하는 답 {52.5, -2.5, 15} 그런데 두개 조건(식)을 그대로 두고 나머지 하나를 변형하다 보니 원하는 답이 나오지 않는 상황이 발생하였다고 질문하신 상황입니다. 3개의 조건식이 주어진 3원 1차 연립방정식은 조건을 변형해서 하나의 변수를 제거할 수 있습니다. 그러면 2개의 조건식으로 주어지는 2원 1차 연립방정식으로 변형할 수 있습니다. (알아보기 더 쉬워서 변형하는 겁니다) 변경하지 않은 조건의 식(con1) 을 이용해 하나의 y & z 1차 방정식을 유도할 수 있는데요. 나머지 방정식이 con1에서 유도된 방정식과 동일해지면 하나의 답이 구해지지 않는 것입니다. 계산기(ti-nspire)는 {x,y,z} 의 답이 하나가 아니고 무수히 많음을 c1 을 이용해서 표현해 준 것입니다. linear_independence_cond12.tns 2025 12.30