- CASIO 570
[fx-570ES][EX] (복소수) 페이저의 표시 설정 / 입력 / 전환(극좌표, 직교좌표)
※ [570] 시리즈의 복소수 모드(CMPLX) 에 대해 잘 알지 못하신다면, 먼저 기초 정보 글을 읽고 오시기 바랍니다. http://www.allcalc.org/7027
1. 복소수 표시 형식의 설정
- 계산을 위해 복소수&페이저를 입력할 때는 직교좌표나 극좌표 형식 아무 것이나 사용해도 상관 없습니다. 하지만, 그 결과값을 화면에 출력할 때는 사전에 지정된 형식으로만 표시됩니다. 따라서 아래와 같이 원하는 출력형식을 미리 지정해 두십시오.
- 【SHIFT】 【MODE】 【▼】 【3】
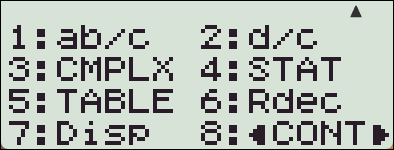
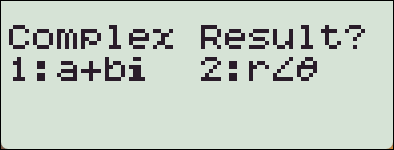
[fx-570EX] 는 【SHIFT】 【MENU】 【▼】 【2】

2. 직교좌표와 극좌표간의 전환 (일시 적용)
【SHIFT】【2】 에서
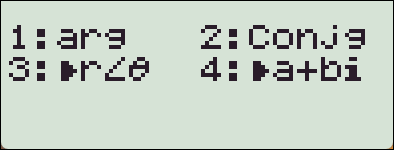
【3】 : 극좌표 형식으로 변환
【4】 : 직교좌표 형식으로 변환
[fx-570 EX] 는
【OPTN】【▼】 후 형식 선택하시면 됩니다.
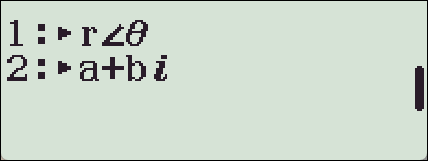
예시 : 결과값(Ans=11+23i) 을 극좌표 형식으로 전환
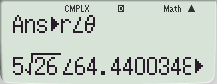
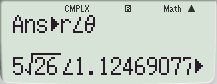
└ 각도 설정 Degree / Radian 에 따라 변환 후 결과 단위가 달라집니다.
※ 복소수값을 이용한 계산없이, 좌표변환만 필요한 경우에는,
[fx-350]과 같이 COMP 모드에서 Pol(), Rect() 함수를 이용해 값을 구할 수도 있습니다.
http://www.allcalc.org/7902
댓글2
-
세상의모든계산기
[EX] Math IO / Line IO 에 따른 차이
【SHIFT】【MENU】(SETUP)
【1】Input / Output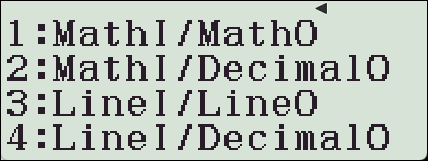
1 : MathI / MathO
 【S⇔D】
【S⇔D】
2: MathI / LineO
 【S⇔D】
【S⇔D】
3: LineI/MathO
4: LineI/LineO

【S⇔D】눌러도 변함 없음.


세상의모든계산기 님의 최근 댓글
오류 발생 https://www.youtube.com/watch?v=dcg0x5SjETY 위 영상의 문제의 함수를 직접 구해 보았습니다. 그래프로는 잘 확인이 되는데... fmin(), fmax() 함수로 직접 구해보니, 결과가 기대한 것과 다르네요. 구간을 넣지 않으니 fmim, fmax 둘 다에서 오류인 결과를 내놓습니다. 구간을 넣더라도, 적절하게 넣지 않으면, 답이 잘 안나오는 걸 확인할 수 있습니다. fmin 은 그나마 x=0을 기준으로 나누지 않더라도 답이 나오는 편이지만, fmax 는 -10~10 을 구간으로 넣을 때, 가운데 x=0 근방에서 그래프가 위로 솟아오르는 구간은 함수값을 확인하지 않는 듯 합니다. ㄴ fmax가 더 열등해서 그런 것은 아니고, 뒤집어진 모양에서는 반대로 fmin이 못찾습니다. 구간 범위가 커질 경우, 함수에 적용하여 계산하다가 숫자 허용 한계를 벗어나서 overflow 가 나서 오류가 발생할 수도 있는 듯 합니다. 뒤에 점을 넣으니 경고 문구가 추가로 나오긴 했는데, ⚠️ Questionable accuracy. When applicable, try using graphical methods to verify the results. 그래도 실망이네요. * 믿음직한 녀석은 아닌 듯 하니, 주의 표시 ⚠️가 나오든 안나오든, 사용에 주의하시기 바랍니다. 가급적이면 그래프로 검증해 보시는게 좋겠습니다. 2025 10.26 예시 8-1 : 분수식 solve시 오류 예시, 분모에 들어간 X³을 X로 치환해 해결? https://allcalc.org/56074 2025 10.25 fx-570 CW 는 아래 링크에서 https://allcalc.org/56026 2025 10.24 불러오기 할 때 변수값을 먼저 확인하고 싶을 때는 VARIABLE 버튼 【⇄[x]】목록에서 확인하고 Recall 하시면 되고, 변수값을 이미 알고 있을 때는 바로 【⬆️SHIFT】【4】로 (A)를 바로 입력할 수 있습니다. 2025 10.24 fx-570 CW 로 계산하면? - 최종 확인된 결과 값 = 73.049507058478629343538 (23-digits) - 오차 = 6.632809104889414877 × 10^-19 꽤 정밀하게 나온건 맞는데, 시뮬레이션상의 22-digits 와 오차 수준이 비슷함. 왜 그런지는 모르겠음. - 계산기중 정밀도가 높은 편인 HP Prime CAS모드와 비교해도 월등한 정밀도 값을 가짐. 2025 10.24