복잡한 다항식 수식에서 계산기 유효 자릿수에 따른 approx() 오차
TI-nspire 기종에 대한 solve 질문글에 대해 답변을 하던 중 이상한 점을 발견하였습니다.
https://allcalc.org/55823
평소에는 방정식의 해를 numeric 한 방식으로 solve 를 이용해 찾는 것보다,
(소숫점을 없애서) exact 방식으로 참 값을 먼저 구하고 → 그 값에 대한 근사값 approx(참 값) 을 구하는 것이 더 정확했습니다.
그런데 이번에는 반대로 오차가 커지는 겁니다.
이 궁금증을 해결하기 위해 직접 분석을 진행해 보았습니다.

1. 분석 대상 수식
분석에 사용된 수식은 다음과 같습니다. cos, sin의 단위는 모두 degree입니다.
$$ \dfrac{120 \left( 150000 \left( \cos\left(\dfrac{7001}{5000}\right) \sqrt{2} - 2 \sin\left(\dfrac{217999}{5000}\right) \right) \cos\left(\dfrac{217999}{5000}\right) - 136342 \sin\left(\dfrac{217999}{5000}\right) \cos\left(\dfrac{7001}{5000}\right) - \left( 150000 \sin\left(\dfrac{7001}{5000}\right) \sin\left(\dfrac{217999}{5000}\right) - 68171 \right) \sqrt{2} \right)}{\sin\left(\dfrac{7001}{5000}\right) \left( 150000 \cos\left(\dfrac{7001}{5000}\right) \cos\left(\dfrac{217999}{5000}\right) - 150000 \sin\left(\dfrac{7001}{5000}\right) \sin\left(\dfrac{217999}{5000}\right) + 68171 \right)} $$
((120*(150000*(cos(((7001)/(5000)))*√(2)-2*sin(((217999)/(5000))))*cos(((217999)/(5000)))-136342*sin(((217999)/(5000)))*cos(((7001)/(5000)))-(150000*sin(((7001)/(5000)))*sin(((217999)/(5000)))-68171)*√(2)))/(sin(((7001)/(5000)))*(150000*cos(((7001)/(5000)))*cos(((217999)/(5000)))-150000*sin(((7001)/(5000)))*sin(((217999)/(5000)))+68171)))
2. 가장 정확한 기준값은? (고정밀도 계산)
오차를 측정하려면 가장 정확한 '참값'이 필요합니다. 일반적인 PC 계산 환경(64비트 float)의 한계를 넘어서기 위해, 파이썬의 mpmath 라이브러리를 사용하여 100자리의 정밀도로 기준값을 계산했습니다.
기준값 (100자리 정밀도):
73.04950705847862934420128091048894148771096960598761210206551516481655390211661403804814403351531886
3. 최종 정밀도 분석표
위 100자리 고정밀도 기준값을 바탕으로, 각기 다른 십진수 유효자릿수를 가진 가상의 계산기를 시뮬레이션하여, 오차를 측정한 결과입니다.
------------------------------------------------------------------------------------------
기준값 (mpmath 100자리): 73.04950705847862934420128091048894148771096960598761210206551516481655390211661403804814403351531886
------------------------------------------------------------------------------------------
유효자릿수 | 시뮬레이션 계산 결과 | 실제 오차 (절대값)
------------------------------------------------------------------------------------------
6 | 73.0496 | 0.0000929415213705222166847666122236
7 | 73.05274 | 0.00323294152137066489366610724034
8 | 73.049758 | 0.00025094152137065247515544299319
9 | 73.0494926 | 0.0000144584786293447601893855457378
10 | 73.04950392 | 0.00000313847862934422482624283943565
11 | 73.049507264 | 0.000000205521370655802788174857506077
12 | 73.0495070344 | 0.0000000240786293442009088985191012186
13 | 73.04950705634 | 0.00000000213862934420122992156882411472
14 | 73.049507058547 | 6.8370655798718306374102620489e-11
15 | 73.0495070585241 | 4.54706557987191402555162474671e-11
16 | 73.04950705847651 | 2.11934420128089909820778774776e-12
17 | 73.049507058478403 | 2.263442012809062555690176752e-13
18 | 73.0495070584786359 | 6.55579871908965212938025673134e-15
19 | 73.04950705847863067 | 1.32579871908948155385084562584e-15
20 | 73.049507058478629386 | 4.17987190895119656392043225004e-17
21 | 73.049507058478629312 | 3.22012809104888423825358781415e-17
22 | 73.04950705847862934452 | 3.18719089511043124817045362596e-19
23 | 73.049507058478629344148 | 5.32809104889360986718490925566e-20
------------------------------------------------------------------------------------------
참고: 표준 64비트 float 계산
- 계산 결과: 73.04950705847811
- 실제 오차: 5.16135835013993051626500528352e-13
------------------------------------------------------------------------------------------
4. 왜 이런 오차가 발생할까?
컴퓨터의 숫자 저장 방식: 2진법의 한계
가장 근본적인 원인은 컴퓨터가 숫자를 2진법으로 저장하는 데 있습니다. 우리가 사용하는 10진수 소수 중 상당수는 2진수로 변환하면 무한소수가 되어, 정해진 비트(bit) 안에 완벽하게 담지 못하고 근사치로 저장됩니다. 이 작은 근사 오차가 계산 과정에서 계속 누적되어 최종 결과에 영향을 미칩니다.
누적 오차의 예시
(1 / 3) * 3 을 유효자릿수 4자리 계산기로 계산하는 상황을 가정해 봅시다.
1 / 3계산: 결과는0.333333...이지만, 4자리만 저장할 수 있으므로0.3333으로 반올림됩니다. (첫 오차 발생)0.3333 * 3계산: 결과는0.9999가 됩니다. 참값인1.0과 미세한 차이가 생깁니다.
복잡한 수식은 이런 과정이 수십, 수백 번 반복되는 것과 같으므로 작은 오차들이 모여 눈에 띄는 차이를 만들게 됩니다.
문제가 된 처음의 수식 역시 계산기 입장에서
* 나눗셈 (Division): 12회
* 분자와 분모의 각 sin, cos 함수 안에 있는 분수 계산 11회
* 마지막에 분자를 분모로 나누는 계산 1회
* 사인 (sin): 7회
* 코사인 (cos): 5회
* 루트 (√): 2회
* 곱셈 (Multiplication): 15회
* 뺄셈 (Subtraction): 5회
* 덧셈 (Addition): 1회
를 모두 계산하는 과정에서 오차가 매번 발생하며 때로는 증폭되기도 하고, 또 누적되기도 하여
최종적으로 solve의 정상 범주를 벗어난 x값이 구해진 것이라고 분석할 수 있겠습니다.
결론
일반적인 공학용 계산기(보통 10~14자리)의 정밀도는 대부분의 상황에서 충분히 신뢰할 만합니다. 하지만 이번 분석처럼 매우 복잡한 연산을 하거나, 과학/금융 분야에서 극도의 정밀도를 요구할 때는 표준 계산 환경의 한계를 인지하는 것이 중요합니다.
이러한 한계를 극복하기 위해 파이썬의 mpmath와 같은 임의 정밀도 산술 라이브러리가 존재하며, 이를 통해 우리는 하드웨어의 제약을 넘어 원하는 만큼 정밀한 값을 얻을 수 있습니다.
부록: 분석에 사용된 전체 Python 코드
이 분석을 직접 재현해보고 싶으신 분들을 위해, 최종 분석에 사용된 전체 코드를 공유합니다. (mpmath 라이브러리 설치가 필요합니다: pip install mpmath)
import math
import sys
from mpmath import mp
def calculate_simulation(precision=None):
"""
Simulates the calculation with intermediate rounding to a specific number of significant digits.
Uses mpmath to perfectly model a calculator with 64-bit float internal precision.
If precision is None, performs a standard 64-bit float calculation without intermediate rounding.
"""
if precision is None:
# This block calculates the result using standard python floats (64-bit)
# to compare the standard float result with the high-precision one.
c_120, c_150000, c_7001, c_5000, c_2, c_217999, c_136342, c_68171 = \
120.0, 150000.0, 7001.0, 5000.0, 2.0, 217999.0, 136342.0, 68171.0
angle1_rad = math.radians(7001.0 / 5000.0)
angle2_rad = math.radians(217999.0 / 5000.0)
cos_a1, sin_a1, cos_a2, sin_a2, sqrt_2 = \
math.cos(angle1_rad), math.sin(angle1_rad), math.cos(angle2_rad), math.sin(angle2_rad), math.sqrt(2.0)
termA = c_150000 * (cos_a1 * sqrt_2 - c_2 * sin_a2)
mul_term1 = termA * cos_a2
termB = c_136342 * sin_a2 * cos_a1
termC = (c_150000 * sin_a1 * sin_a2 - c_68171) * sqrt_2
numerator = c_120 * (mul_term1 - termB - termC)
inner_den_final = (c_150000 * cos_a1 * cos_a2) - (c_150000 * sin_a1 * sin_a2) + c_68171
denominator = sin_a1 * inner_den_final
return (numerator / denominator) if denominator != 0 else float('inf')
# --- High-precision simulation that mimics a 64-bit float calculator ---
# If p < 17, use 53-bit precision to mimic float.
# If p >= 17, use enough bits to handle 'p' decimal digits.
working_prec = 53 if precision < 17 else int(precision * 3.4) + 20
def apply_prec(value):
"""Rounds the mp.mpf 'value' to 'precision' significant digits in a high-precision context."""
if value == 0:
return mp.mpf(0)
# Perform the rounding operation in a temporary high-precision context
with mp.workdps(precision + 10):
return mp.mpf(mp.nstr(value, n=precision))
# Perform the main calculation in the determined working precision
with mp.workprec(working_prec):
c_120, c_150000, c_7001, c_5000, c_2, c_217999, c_136342, c_68171 = \
mp.mpf(120), mp.mpf(150000), mp.mpf(7001), mp.mpf(5000), mp.mpf(2), \
mp.mpf(217999), mp.mpf(136342), mp.mpf(68171)
angle1_deg = apply_prec(c_7001 / c_5000)
angle2_deg = apply_prec(c_217999 / c_5000)
angle1_rad = apply_prec(mp.radians(angle1_deg))
angle2_rad = apply_prec(mp.radians(angle2_deg))
cos_a1, sin_a1, cos_a2, sin_a2, sqrt_2 = \
apply_prec(mp.cos(angle1_rad)), apply_prec(mp.sin(angle1_rad)), \
apply_prec(mp.cos(angle2_rad)), apply_prec(mp.sin(angle2_rad)), \
apply_prec(mp.sqrt(c_2))
termA_inner_part1 = apply_prec(cos_a1 * sqrt_2)
termA_inner_part2 = apply_prec(c_2 * sin_a2)
termA_inner_sub = apply_prec(termA_inner_part1 - termA_inner_part2)
termA = apply_prec(c_150000 * termA_inner_sub)
mul_term1 = apply_prec(termA * cos_a2)
termB = apply_prec(apply_prec(c_136342 * sin_a2) * cos_a1)
termC_inner_sub = apply_prec(apply_prec(apply_prec(c_150000 * sin_a1) * sin_a2) - c_68171)
termC = apply_prec(termC_inner_sub * sqrt_2)
numerator = apply_prec(c_120 * apply_prec(apply_prec(mul_term1 - termB) - termC))
den_term1 = sin_a1
den_term2 = apply_prec(apply_prec(c_150000 * cos_a1) * cos_a2)
den_term3 = apply_prec(apply_prec(c_150000 * sin_a1) * sin_a2)
inner_den_final = apply_prec(apply_prec(den_term2 - den_term3) + c_68171)
denominator = apply_prec(den_term1 * inner_den_final)
final_result = apply_prec(numerator / denominator) if denominator != 0 else mp.inf
return final_result
# --- High-Precision Ground Truth Function (from high_precision_calc.py) ---
def get_high_precision_ground_truth():
"""Calculates the ground truth with 100 digits of precision using mpmath."""
mp.dps = 100
c_120, c_150000, c_7001, c_5000, c_2, c_217999, c_136342, c_68171 = \
mp.mpf(120), mp.mpf(150000), mp.mpf(7001), mp.mpf(5000), mp.mpf(2), \
mp.mpf(217999), mp.mpf(136342), mp.mpf(68171)
angle1_rad = mp.radians(c_7001 / c_5000)
angle2_rad = mp.radians(c_217999 / c_5000)
cos_a1, sin_a1, cos_a2, sin_a2, sqrt_2 = \
mp.cos(angle1_rad), mp.sin(angle1_rad), mp.cos(angle2_rad), mp.sin(angle2_rad), mp.sqrt(c_2)
termA = c_150000 * (cos_a1 * sqrt_2 - c_2 * sin_a2)
mul_term1 = termA * cos_a2
termB = c_136342 * sin_a2 * cos_a1
termC = (c_150000 * sin_a1 * sin_a2 - c_68171) * sqrt_2
numerator = c_120 * (mul_term1 - termB - termC)
inner_den_final = (c_150000 * cos_a1 * cos_a2) - (c_150000 * sin_a1 * sin_a2) + c_68171
denominator = sin_a1 * inner_den_final
return numerator / denominator
# --- Main Execution ---
if __name__ == "__main__":
# 1. Get the high-precision ground truth
ground_truth = get_high_precision_ground_truth()
print("### 최종 정밀도 분석표 (100자리 기준값 사용) ###")
print("-" * 90)
print(f"기준값 (mpmath 100자리): {ground_truth}")
print("-" * 90)
print(f"{ '유효자릿수':<12} | {'시뮬레이션 계산 결과':<45} | {'실제 오차 (절대값)':<30}")
print("-" * 90)
# 2. Run the simulation loop and compare against the new ground truth
for p in range(6, 23):
sim_result = calculate_simulation(precision=p)
# Perform the error calculation in a high-precision context
with mp.workdps(100):
error = abs(sim_result - ground_truth)
# Format the error to 30 decimal places for printing
with mp.workdps(30):
error_str = str(error)
print(f"{p:<12} | {mp.nstr(sim_result, n=p):<45} | {error_str}")
print("-" * 90)
# 3. Analyze the standard float result against the ground truth
standard_float_result = calculate_simulation() # No precision limit
# Perform the error calculation in a high-precision context
with mp.workdps(100):
standard_float_error = abs(mp.mpf(standard_float_result) - ground_truth)
# Format the error to 30 decimal places for printing
with mp.workdps(30):
standard_float_error_str = str(standard_float_error)
print(f"참고: 표준 64비트 float 계산")
print(f" - 계산 결과: {standard_float_result}")
print(f" - 실제 오차: {standard_float_error_str}")
print("-" * 90)댓글6
-
세상의모든계산기
카시오 fx-570 ES, EX 로 계산하면?
카시오도 (십진수) 14digits 한계이므로, 비슷한 값이 나올 것으로 예상됨.다만, stack 및 길이 한계로 수식 전체를 그대로 입력할 수는 없음.
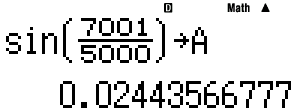
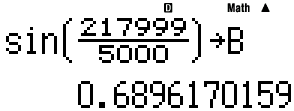
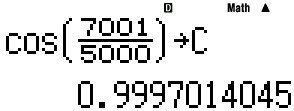
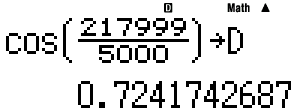
A,B,C,D 를 조합해 수식을 완성
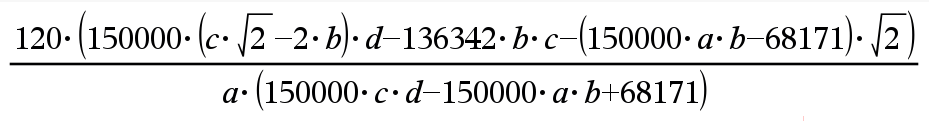
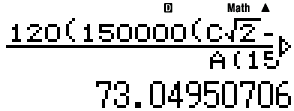
결과에서 73.049507 을 빼면
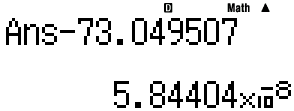
- fx-570 ES가 구한 결과값(Ans)은
73.0495070584404 (15digits) 로 최종 확인됨.
- TI-Nspire (14-digits) 보다 오차가 작음.
- 파이썬 시뮬레이션의 15-digits 결과(73.0495070585241)와 같지는 않음. 원인은 모르겠음.
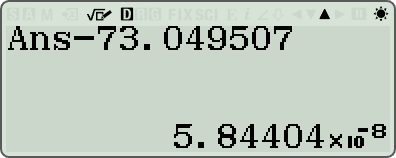
ㄴ fx-570 EX 결과
-
세상의모든계산기
TI-nspire 에서 동일하게 a,b,c,d로 치환해서 계산
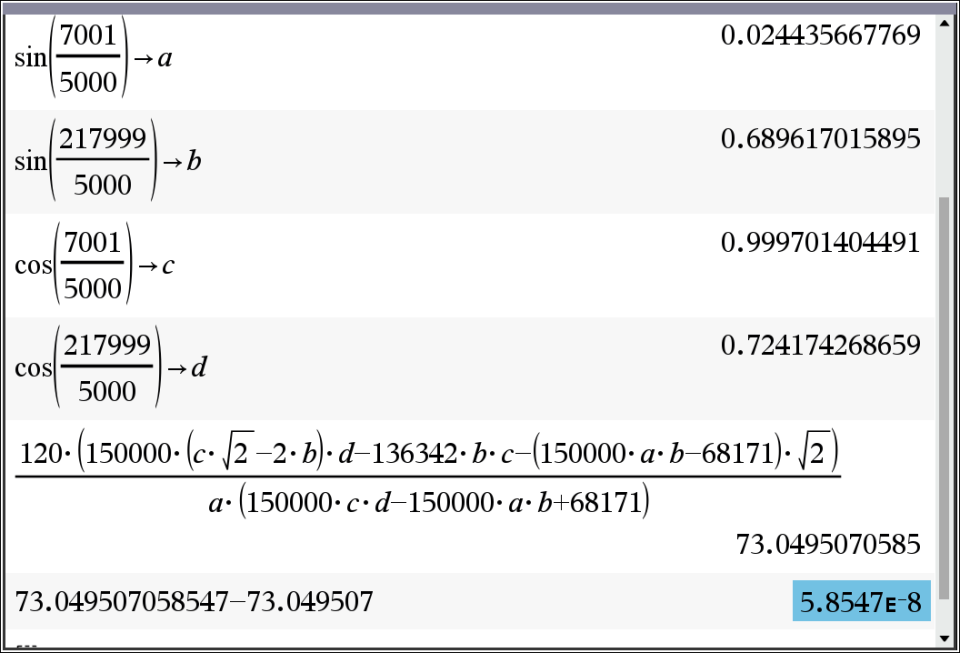
- 결과는 치환 없이 그냥 approx(전체식) 한 결과와 동일.
- 73.049507058547 (14-digits)
- 파이썬 시뮬레이션 14-digits 와 결과값이 같음.
-
세상의모든계산기
fx-9860 및 fx-CG 의 경우
fx-9860GII SD 에서 위의 fx-570 과 같이 A,B,C,D 로 나눠서 계산하면

fx-CG에서 치환할 대상을 약간 바꿔서 분모→A, 분자→B 로 저장해 풀어보아도

- 결과는 둘 다 같음.
- 73.0495070585238 (15 digits)
- fx-570ES와 같은 15-decimal-digits 정밀도인데, 왜 값이 다를까?
- 파이썬 시뮬레이터상 15 digits 값과도 같지 않음.
-
세상의모든계산기
fx-570 CW 로 계산하면?
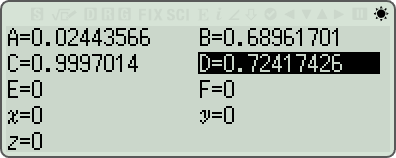
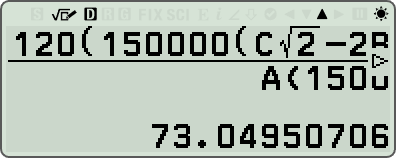
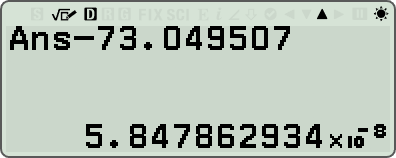
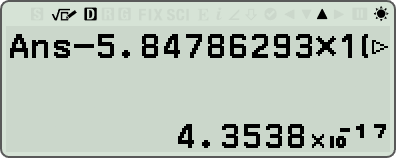
- 최종 확인된 결과 값 = 73.049507058478629343538 (23-digits)
- 오차 = 6.632809104889414877 × 10^-19
꽤 정밀하게 나온건 맞는데, 시뮬레이션상의 22-digits 와 오차 수준이 비슷함. 왜 그런지는 모르겠음.
- 계산기중 정밀도가 높은 편인 HP Prime CAS모드와 비교해도 월등한 정밀도 값을 가짐.
-
세상의모든계산기
HP Prime 에서
<Home>
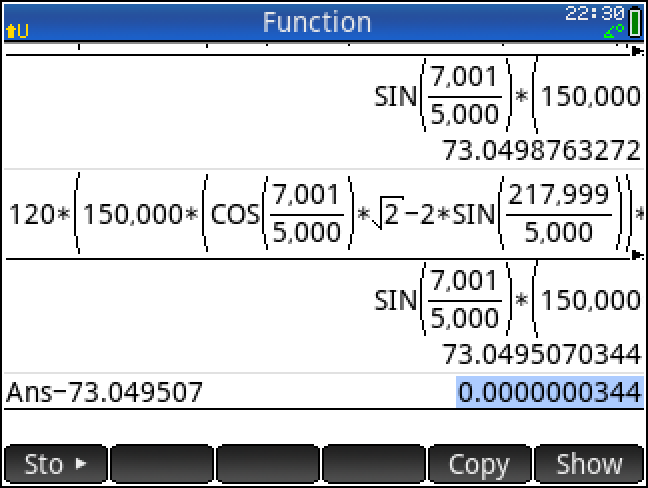
73.0495070344 (12-decimal-digits) // python 시뮬레이션과 일치
<CAS>
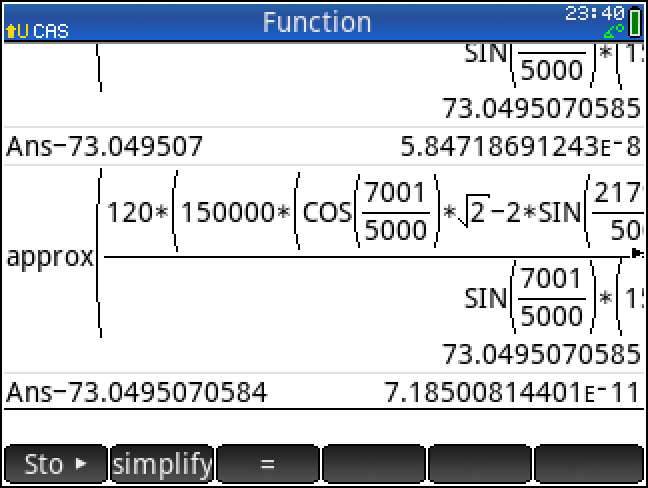
21자리까지 나와서 이상하다 싶었는데,
Ans- 에서 자릿수를 더 늘려서 빼보니, 뒷부분 숫자가 아예 바뀌어버림. 버그인가?
(전) 73.0495070584718691243 (21-digits ????)
(후) 73.0495070584718500814401 (24-digits ????)
찾아보니 버그는 아니고,
CAS에서는 십진수가 아니라 2진수(bit) 단위로 처리한다고 함.
Giac uses 48 bits mantissa from the 53 bits from IEEE double. The reason is that Giac stores CAS data (gen type) in 64 bits and 5 bits are used for the data type (24 types are available). We therefore loose 5 bits (the 5 low bits are reset to 0 when a double is retrieved from a gen).
출처 : https://www.hpmuseum.org/cgi-bin/archv021.cgi?read=255657
일단 오차를 놓고 보면 16-decimal-digits 수준으로 보임.


세상의모든계산기 님의 최근 댓글
불러오기 할 때 변수값을 먼저 확인하고 싶을 때는 VARIABLE 버튼 【⇄[x]】목록에서 확인하고 Recall 하시면 되고, 변수값을 이미 알고 있을 때는 바로 【⬆️SHIFT】【4】로 (A)를 바로 입력할 수 있습니다. 2025 10.24 fx-570 CW 로 계산하면? - 최종 확인된 결과 값 = 73.049507058478629343538 (23-digits) - 오차 = 6.632809104889414877 × 10^-19 꽤 정밀하게 나온건 맞는데, 시뮬레이션상의 22-digits 와 오차 수준이 비슷함. 왜 그런지는 모르겠음. - 계산기중 정밀도가 높은 편인 HP Prime CAS모드와 비교해도 월등한 정밀도 값을 가짐. 2025 10.24 HP Prime 에서 <Home> 73.0495070344 (12-decimal-digits) // python 시뮬레이션과 일치 <CAS> 21자리까지 나와서 이상하다 싶었는데, Ans- 에서 자릿수를 더 늘려서 빼보니, 뒷부분 숫자가 아예 바뀌어버림. 버그인가? (전) 73.0495070584718691243 (21-digits ????) (후) 73.0495070584718500814401 (24-digits ????) 찾아보니 버그는 아니고, CAS에서는 십진수가 아니라 2진수(bit) 단위로 처리한다고 함. Giac uses 48 bits mantissa from the 53 bits from IEEE double. The reason is that Giac stores CAS data (gen type) in 64 bits and 5 bits are used for the data type (24 types are available). We therefore loose 5 bits (the 5 low bits are reset to 0 when a double is retrieved from a gen). 출처 : https://www.hpmuseum.org/cgi-bin/archv021.cgi?read=255657 일단 오차를 놓고 보면 16-decimal-digits 수준으로 보임. 2025 10.23 khiCAS 에서 HP 39gII 에 올린 khiCAS는 254! 까지 계산 가능, 255! 부터는 ∞ fx-9750GIII 에 올린 khiCAS는 factorial(533) => 425760136423128437▷ // 정답, 10진수 1224자리 factorial(534) => Object too large 2025 10.23 같은 방식으로 500! 근사값을 구해보면 1.219933487 × 10^(1134) 1.22013682599111006870123878542304692625357434280319284219241358838 × 10^(1134) (참값, 울프람 알파) 2025 10.23