- CASIO 570
[fx-570ES] STAT 통계 - 편차제곱의 합. SSX 또는 SSY
편차제곱의 합은 통계학에서 데이터의 분산과 표준편차를 계산할 때 중요한 개념입니다. 이를 이해하기 위해 먼저 편차를 정의해야 합니다.

1. 편차 (Deviation):
편차는 각 데이터 값이 평균에서 얼마나 떨어져 있는지를 나타내는 값입니다. 수식으로는 다음과 같습니다.
\[
\text{편차} = x_i - \mu
\]
여기서:
- \( x_i \)는 각 데이터 값
- \( \mu \)는 데이터 값들의 평균입니다.
2. 편차제곱 (Squared Deviation):
편차는 양수 또는 음수일 수 있기 때문에, 이 값들을 제곱하여 편차제곱을 구합니다. 이는 음수와 양수를 구분하지 않고 편차의 크기만을 평가할 수 있게 합니다.
\[
\text{편차제곱} = (x_i - \mu)^2
\]
3. 편차제곱의 합 (Sum of Squared Deviations):
편차제곱을 모든 데이터에 대해 구한 후, 이들을 모두 더한 값이 편차제곱의 합입니다. 이는 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내는 중요한 값입니다.
\[
\text{편차제곱의 합} = \sum_{i=1}^{n} (x_i - \mu)^2
\]
이 값은 분산(Variance) 및 표준편차(Standard Deviation)를 구하는 데 사용됩니다.
- 분산은 편차제곱의 합을 데이터 개수로 나눈 값입니다.
- 표준편차는 분산의 제곱근입니다.
- 약어 표시
- SSX: 독립 변수 XXX에 대한 편차제곱의 합 (Sum of Squares for XXX).
- SST: 총 편차제곱의 합 (Total Sum of Squares).
- SSR: 회귀의 편차제곱의 합 (Sum of Squares for Regression).
- SSE: 잔차의 편차제곱의 합 (Sum of Squares for Error).
4. SSX와 기본 통계 변수들 간의 관계
1. SSX와 평균:
- SSX는 변수 X의 각 데이터 값이 평균 $ \mu \ $ 에서 얼마나 떨어져 있는지를 제곱한 값의 합입니다. 즉, 편차를 제곱하고 모두 더한 것이 SSX입니다.
\[
SSX = \sum_{i=1}^{n} (x_i - \bar{x})^2
\]
여기서 \(x_i\)는 각 데이터 값, \(\bar{x}\)는 데이터의 평균입니다.
2. SSX와 분산:
- 분산(Variance)은 SSX를 데이터 개수 \(n\)로 나눈 값입니다.
\[
\text{분산} (\sigma^2) = \frac{SSX}{n}
\]
분산은 데이터 값들이 평균에서 얼마나 퍼져 있는지를 나타내는 지표로, SSX를 표본 크기 \(n\)으로 나누어 계산합니다.
만약 표본 분산(sample variance)을 구하려면 \(n\) 대신 \(n - 1\)을 사용합니다.
\[
\text{표본 분산} (s^2) = \frac{SSX}{n - 1}
\]
3. SSX와 표준편차:
- 표준편차(Standard Deviation)는 분산의 제곱근입니다. 따라서, SSX를 이용해 분산을 구한 후, 표준편차를 구할 수 있습니다.
\[
\text{표준편차} (\sigma) = \sqrt{\frac{SSX}{n}}
\]
표본 표준편차(sample standard deviation)의 경우도 마찬가지로 표본 분산의 제곱근을 구합니다.
\[
\text{표본 표준편차} (s) = \sqrt{\frac{SSX}{n - 1}}
\]
요약
SSX는 기본 통계 변수들과 다음과 같은 관계를 가집니다:
- SSX는 평균에서 각 데이터 값들의 편차제곱을 모두 더한 값입니다.
- 분산은 SSX를 데이터의 개수로 나눈 값이며, 데이터 값들의 변동성을 나타냅니다.
- 표준편차는 SSX를 기반으로 구한 분산의 제곱근으로, 데이터가 평균에서 얼마나 퍼져 있는지 보여줍니다.
예시
- 데이터: \( [2, 4, 6, 8] \)
- 평균: \( \bar{x} = 5 \)
- SSX:
\[
SSX = (2-5)^2 + (4-5)^2 + (6-5)^2 + (8-5)^2 = 9 + 1 + 1 + 9 = 20
\]
- 분산: \( \sigma^2 = \frac{SSX}{n} = \frac{20}{4} = 5 \)
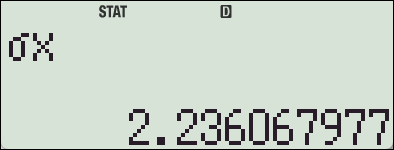
- 표준편차: \( \sigma = \sqrt{5} \approx 2.236 \)


 : 1-VAR
: 1-VAR








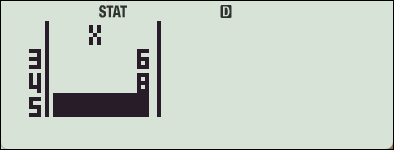



 : Var
: Var
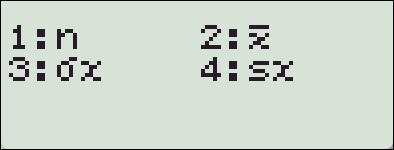
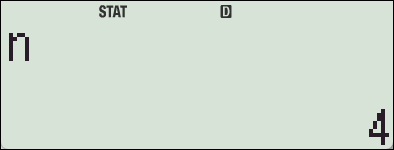
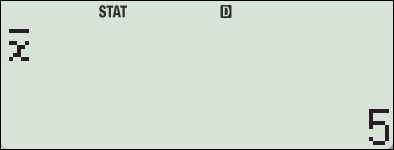

4. fx-570 ES 기종에서의 SSX, SSY
카시오 fx-570ES Plus 계산기에는 편차제곱의 합 (SSX, Sum of Squared Deviations)을 직접 구해주는 함수나 변수가 내장되어 있지 않습니다.
https://allcalc.org/5615 - [fx-570][fx-350] STAT 통계 모드 진행 과정 (변수 분석, 회귀 분석 등 전반)
일반적으로 통계 계산을 위해 제공되는 주요 기능들은 평균, 분산, 표준편차 등을 계산하는 것이기 때문에,
표준편차의 계산을 위한 중간 과정인 '분산'이나 '편차제곱의 합'은 통계 변수로 따로 저장되지 않았습니다.
(어떤 변수를 저장할지의 결정은 계산기 모델마다 다를 수 있습니다)
따라서 위에서 일일이 따로 계산하거나, 위의 공식(2. 분산) 을 반대로 계산하여 이미 계산되어 저장된 통계변수를 활용하여 값을 구할 수 있습니다.
\[
\text{편차제곱의 합}, SSX = \sigma^2 \cdot n = s^2 \cdot \left(n - 1\right)
\]




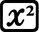






댓글1
-
세상의모든계산기
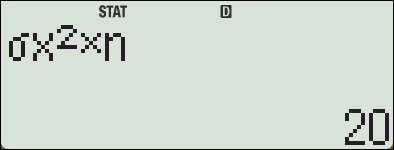
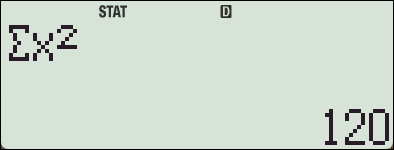
편차제곱의 합 SS 와
Sum 목록에 있는 x^2의 합은 서로 다른 값입니다.


 : Sum
: Sum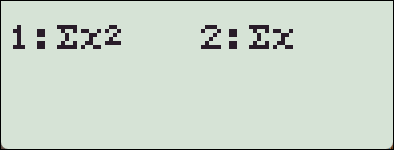



세상의모든계산기 님의 최근 댓글
[공학용 계산기] 빼기 기호 【-】 와 음수 기호 【(-)】 의 구분 https://allcalc.org/5876 2025 10.26 [BA II PLUS] 로 입력해 보니 [EL-738XT] 과 달리 【+|-】 버튼을 이용하든 【-】버튼을 이용하든 앞에 입력된 항목값은 음수 입력에 영향을 주지 않네요. 2025 10.26 오류 발생 https://www.youtube.com/watch?v=dcg0x5SjETY 위 영상의 문제의 함수를 직접 구해 보았습니다. 그래프로는 잘 확인이 되는데... fmin(), fmax() 함수로 직접 구해보니, 결과가 기대한 것과 다르네요. 구간을 넣지 않으니 fmim, fmax 둘 다에서 오류인 결과를 내놓습니다. 구간을 넣더라도, 적절하게 넣지 않으면, 답이 잘 안나오는 걸 확인할 수 있습니다. fmin 은 그나마 x=0을 기준으로 나누지 않더라도 답이 나오는 편이지만, fmax 는 -10~10 을 구간으로 넣을 때, 가운데 x=0 근방에서 그래프가 위로 솟아오르는 구간은 함수값을 확인하지 않는 듯 합니다. ㄴ fmax가 더 열등해서 그런 것은 아니고, 뒤집어진 모양에서는 반대로 fmin이 못찾습니다. 구간 범위가 커질 경우, 함수에 적용하여 계산하다가 숫자 허용 한계를 벗어나서 overflow 가 나서 오류가 발생할 수도 있는 듯 합니다. 뒤에 점을 넣으니 경고 문구가 추가로 나오긴 했는데, ⚠️ Questionable accuracy. When applicable, try using graphical methods to verify the results. 그래도 실망이네요. * 믿음직한 녀석은 아닌 듯 하니, 주의 표시 ⚠️가 나오든 안나오든, 사용에 주의하시기 바랍니다. 가급적이면 그래프로 검증해 보시는게 좋겠습니다. 2025 10.26 예시 8-1 : 분수식 solve시 오류 예시, 분모에 들어간 X³을 X로 치환해 해결? https://allcalc.org/56074 2025 10.25 fx-570 CW 는 아래 링크에서 https://allcalc.org/56026 2025 10.24