- TI nspire
fmax =함수의 최대값일 때의 x값, fmin =함수의 최소값일 때의 x값
1. fmax() 함수
fMax(Expr, Var) ⇒ Boolean expression
fMax(Expr, Var,lowBound)
fMax(Expr, Var,lowBound,upBound)
fMax(Expr, Var) | lowBound≤Var≤upBound
Expr을 최대화하는 Var의 후보 값, 또는 최대값이 없을 경우 최소 상한(least upper bound)이 되는 Var의 후보 값을 정의하는 부울리언 표현식을 반환합니다.
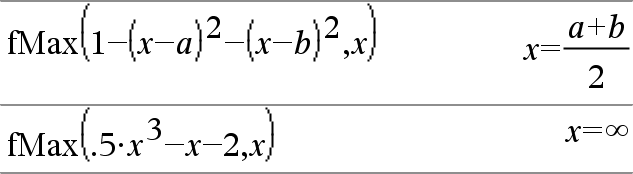
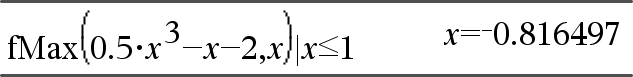
제약 연산자("|")를 사용하여 해의 구간을 제한하거나 다른 제약 조건을 지정할 수 있습니다.
'자동(Auto)' 또는 '근사(Approximate)' 모드에서 '근사(Approximate)'로 설정한 경우, fMax() 함수는 반복적인 계산을 통해 하나의 근사적인 극댓값(approximate local maximum)을 찾습니다.
특히, "|" 연산자로 검색 구간을 하나의 극댓값만 포함하는 작은 범위로 제한하면 계산 속도가 더 빨라집니다.
2. fmin() 함수
fMin(Expr, Var) ⇒ Boolean expression
fMin(Expr, Var,lowBound)
fMin(Expr, Var,lowBound,upBound)
fMin(Expr, Var) | lowBound≤Var≤upBound
Expr을 최소화하는 Var의 후보 값, 또는 최소값이 없을 경우 최대 하한(greatest lower bound)이 되는 Var의 후보 값을 정의하는 부울리언 표현식을 반환합니다.
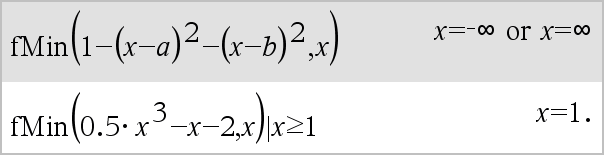
제약 연산자("|")를 사용하여 해의 구간을 제한하거나 다른 제약 조건을 지정할 수 있습니다.
'자동(Auto)' 또는 '근사(Approximate)' 모드에서 '근사(Approximate)'로 설정한 경우,
fMin() 함수는 반복적인 계산을 통해 하나의 근사적인 극솟값(approximate local minimum)을 찾습니다.
특히, "|" 연산자로 검색 구간을 하나의 극솟값만 포함하는 작은 범위로 제한하면 계산 속도가 더 빨라집니다.
3. 주의
위 두 함수는 최대(최소상한), 최소(최대하한) 이 되는 함수값 f(x) 를 계산해서 보여주는 함수가 아닙니다.
그 때의 x 값을 구하는 함수입니다.
함수값 f(x) 를 구하는 함수는 없으니, 찾아진 부울리언 표현식 f(x)에 제약연산자로 넣어서 계산하시면 됩니다.

- 계산기의 한계 :
fMin/fMax 기능은 댓글의 예제와 같이 복잡한 함수에 대해 넓은 구간 또는 무한 구간을 탐색할 때 수치적으로 불안정하거나 잘못된 결과를 내놓는 한계를 가지고 있습니다.
- 문제의 해결 :
그래프 기능으로 함수의 개형을 미리 확인하고, 검색 구간을 좁혀서 계산기를 '가이드' 하는 것이 바람직해 보입니다.
아니면 미분&solve 기능을 이용해 극값을 갖는 x값을 미리 확인하고, 그 값을 구간의 기준으로 나누어 검색해 보는 것도 방법이 될 수 있을 듯 합니다.
댓글1
-
세상의모든계산기
오류 발생
https://www.youtube.com/watch?v=dcg0x5SjETY
위 영상의 문제의 함수를 직접 구해 보았습니다.
그래프로는 잘 확인이 되는데...
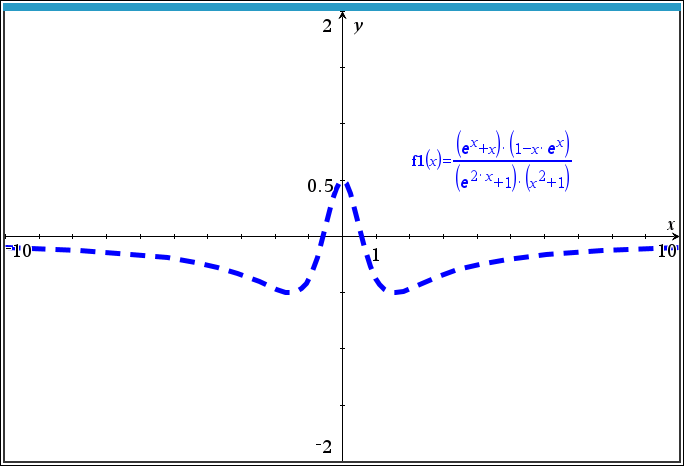

fmin(), fmax() 함수로 직접 구해보니, 결과가 기대한 것과 다르네요.
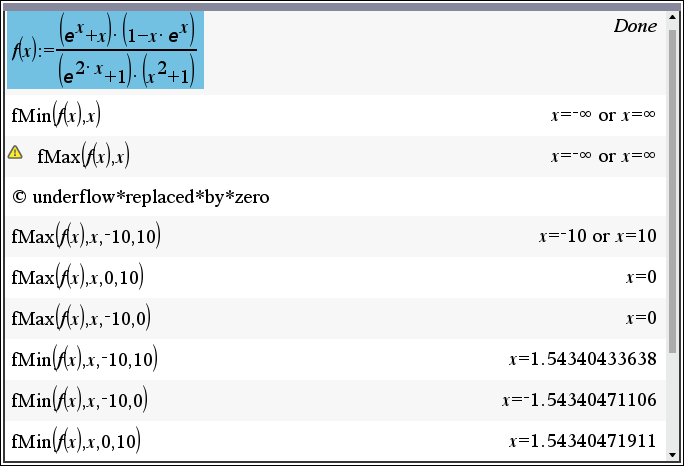
구간을 넣지 않으니 fmim, fmax 둘 다에서 오류인 결과를 내놓습니다.
구간을 넣더라도, 적절하게 넣지 않으면, 답이 잘 안나오는 걸 확인할 수 있습니다.
fmin 은 그나마 x=0을 기준으로 나누지 않더라도 답이 나오는 편이지만,
fmax 는 -10~10 을 구간으로 넣을 때, 가운데 x=0 근방에서 그래프가 위로 솟아오르는 구간은 함수값을 확인하지 않는 듯 합니다.
ㄴ fmax가 더 열등해서 그런 것은 아니고, 뒤집어진 모양에서는 반대로 fmin이 못찾습니다.

구간 범위가 커질 경우, 함수에 적용하여 계산하다가 숫자 허용 한계를 벗어나서 overflow 가 나서 오류가 발생할 수도 있는 듯 합니다.
뒤에 점을 넣으니 경고 문구가 추가로 나오긴 했는데,
⚠️ Questionable accuracy. When applicable, try using graphical methods to verify the results.
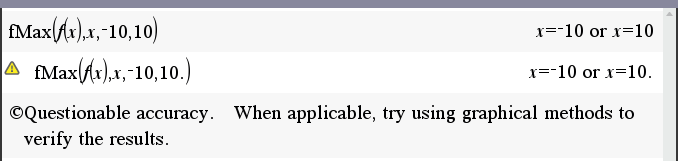
그래도 실망이네요.
* 믿음직한 녀석은 아닌 듯 하니, 주의 표시 ⚠️가 나오든 안나오든, 사용에 주의하시기 바랍니다.
가급적이면 그래프로 검증해 보시는게 좋겠습니다.


세상의모든계산기 님의 최근 댓글
2번 사진 3개 사진 공통적으로 구석(corner) 에 증상이 있다는 특징이 있네요. 영상 찾아보니 이 가능성이 가장 높은 듯 합니다. https://www.youtube.com/watch?v=zxRBohepzwc ㄴ Liquid Crystal Leakage (액정 누설). ㄴ 손으로 밀어내니 주변으로 밀려나네요. 그래서 점으로 보이기도 하구요. 2025 10.29 500! 의 십진수 근사값 확인 500! = 1.22013682599111006870123878542304692625357434280319284219241358838 × 10^(1134) (참값, 울프람 알파) 2025 10.29 관련 라이브러리 https://allcalc.org/56263 sgn(x) 내장된 부호 함수(signum function)와 달리, 이 함수의 sgn(0)은 0을 반환합니다. 2025 10.29 라이브러리로 사용할 수 있습니다. (제작자 추천) 1. mylib 폴더에 넣기 2. Actions ➡️ library ➡️ refresh libraries 실행 하기 2025 10.29 ChatGPT-5 기호(÷, /, :) 자체는 의미적으로 같은 “나눗셈”을 뜻하지만, 문맥(사람이 쓰는 수학 vs 컴퓨터/프로그래밍)에 따라 해석 우선순위가 달라질 수 있습니다. 🔹 1️⃣ 전통 수학 표기 — ÷, /, : 수학 교과서, 논문, 일반 문서 등에서는 셋 다 의미적으로 “나누기”로 간주됩니다. 즉, 48÷2(9+3), 48/2(9+3), 48:2(9+3) 은 같은 의미로 받아들여야 합니다. 모두 사람의 수학 관행적 해석이 적용되어 48 ÷ 2 × (9+3) = 288 로 처리되죠. 즉, 기호가 바뀌어도 결과는 바뀌지 않습니다. 🔹 2️⃣ 컴퓨터·프로그래밍 문맥에서 / 사용 시 컴퓨터는 “생략된 곱셈(implicit multiplication)”을 따로 구분하지 못합니다. 따라서 다음 두 식은 완전히 다르게 인식됩니다. 표현 파이썬 등에서 해석 결과 48 / 2*(9+3) ((48 / 2) * (9+3)) 288 48 / 2(9+3) ❌ 문법 오류 (생략된 곱셈 인식 불가) — 즉, 컴퓨터 언어에서는 생략된 곱셈이 허용되지 않기 때문에, /는 반드시 명시적 *와 함께 써야 합니다. 🔹 3️⃣ “:” 기호의 경우 현대 수학에서는 “비율”을 나타내는 기호로 쓰입니다. a:b = \frac{a}{b} 따라서 (27 : 3(1+2)3) 같은 표현은 모호하거나 비표준적으로 간주됩니다. 대부분의 경우 계산기로는 입력 자체가 불가능합니다. ✅ 정리 기호 의미 결과 변화 주로 쓰이는 문맥 ÷ 나누기 없음 초중등 수학, 일반 표기 / 나누기 없음 (단, 프로그래밍에서는 생략 곱 불허) 수학/컴퓨터 : 비율 (또는 나누기 의미로 혼용) 보통 계산식에서는 사용 안 함 비, 비율 표기 🔹 결론 48 ÷ 2(9+3), 48/2(9+3), 48:2(9+3) 는 “수학적 의미”로는 동일하게 81로 해석됩니다. 하지만 프로그래밍이나 수식 파서(context) 에서는 /만 유효하고, 생략된 곱은 허용되지 않으며, :는 아예 다른 의미(비율)로 인식됩니다. 2025 10.28