[ticalc.org 펌] Gamma & Zeta function +more. 감마 제타 함수 외
원본 출처
https://www.ticalc.org/archives/files/fileinfo/415/41529.html
Gamma ver 1.3. by Mauritz Blomqvist (for the Nspire CAS)
This small package does contain implementations of some various special functions like the Gamma function and the Reimann Zeta function.
Some of the functions will return exact values in special cases.
The algorithms are based on information from the Gnu C Scientific library, from NUMERICAL RECIPES, The Art of Scientific Computing, Third Edition, from http://mathworld.wolfram.com/, from various documents mentioned in the files and from own ideas and algorithms.
This version is greatly extended from the version 1.1. In that version I also forgot to set some variables to LibPriv, which meant that some functions did not work outside this library. The basic difference between this version and version 1.2 is the addition of functions related to the Riemann Zeta function.
A suggestion is that you place this in a map under MyLib. Do not forget to update the library access.
Please report errors or comments to me at MauritzTortoise…telia.com where …=@.
설명 번역 :
✦ Mauritz Blomqvist의 감마 버전 1.3 (현재 CAS 및 비 CAS 버전 제공)
이 작은 패키지에는 감마 함수, 리만 제타 함수 및 관련 함수와 같은 다양한 특수 함수의 구현이 포함되어 있습니다. 대부분의 함수에 대해 복소수 인수를 처리할 수 있습니다.
gamma.tns 파일은 CAS용이고 gammanc.tns는 비 CAS용입니다. CAS 버전은 gamma(7/2)와 같은 일부 특수한 경우에 정확한 값을 반환합니다.
함수 소개 번역
✦ Gamma and related functions
gamma(z)
이 작은 패키지는 감마 함수 계산을 위한 란초스 근사(Lanczos approximation) 구현을 포함합니다. 실수 및 복소수 입력 모두에 대해 상당히 정확한 값을 반환합니다.
수식은 다음과 같습니다:
Γ(z)=gamma(z)≡∫(t^(z-1)*e^(-t),t,0,∞)
실수부와 허수부 모두 평균 0, 표준편차 30인 정규분포를 따르는 1000개의 숫자로 테스트한 결과, 상대 오차는 대부분 실수부와 허수부 모두에서 1E-10 이하 수준이었습니다. 가장 큰 상대 오차는 약 4E-8이었습니다.
이 함수는 양의 정수와 ½의 배수에 대해 정확한 값을 반환합니다.
gamma(3.5) 3.323350970447
gamma(((7)/(2))) ((15*√(π))/(8))
gamma(3.) 2.
gamma(3) 2
gamma(((−7)/(2))) ((16*√(π))/(105))
gamma(1+2i) 0.15190400267+0.019804880162*i
gamma(30) 8841761993739701954543616000000
gamma(30.) 8.84176199374E30
------
lngamma(z)
감마의 자연로그입니다. 감마 함수에 큰 인수가 필요할 때 사용할 수 있습니다.
아래 답변은 최소 유효 숫자의 한 단위 내에서 정확합니다.
lngamma(10000) 82099.7174964
일반 감마 함수는 이처럼 큰 입력을 처리할 수 없습니다.
ln(gamma(10000)) ln(9999!)
lngamma(20) ln(5773625)+2*ln(145152)
------
digamma(z)
감마의 로그 미분입니다. 즉, (d/dz)(lngamma(z))입니다.
digamma(1) −0.577215664901
이것은 -γ(오일러-마스케로니 상수)입니다.
-γ −0.577215664902
------
dergamma(z)
감마의 미분입니다.
dergamma(10) 817115.979521
------
doublefactorial(n)
이중 계승(double factorial)입니다. n!!=n*(n-2)*....
doublefactorial(8) 384
doublefactorial(7) 105
------
lowerigamma(a,z)
하 불완전 감마 함수(lower incomplete gamma)를 계산합니다:
γ(a,z)≡∫(t^(a-1)*e^(-t),t,0,z).
------
upperigamma(a,z)
상부 불완전 감마 함수(upper incomplete gamma)를 계산합니다:
Γ(a,z)≡∫(t^(a-1)*e^(-t),t,z,∞).
upperigamma(3,2) 10*e^(−2)
lowerigamma(3,2)+upperigamma(3,2) 2.
upperigamma(10,((3)/(2)))
((832670037*e^(((−3)/(2))))/(512))
------
p(a,z)
정규화된 하부 불완전 감마 함수(regularized incomplete lower gamma)를 계산합니다.
((γ(a,z))/(Γ(a))).
------
q(a,z)
정규화된 상부 불완전 감마 함수(regularized incomplete upper gamma)를 계산합니다.
((Γ(a,z))/(Γ(a))).
------
invp(pr,a)
p의 역함수입니다.
invp(p(2.2,3.4),2.2) 3.4
------
erf(z)
오차 함수(error function)입니다. 불완전 감마 함수를 기반으로 하며, 내장된 normCdf 함수를 기반으로 하는 것보다 정확도가 더 높습니다.
erf(1.3) 0.934007944941
2*normCdf(−∞,1.3*√(2),0,1)-1 0.934008064885
첫 번째 결과는 올바르게 반올림된 답, 즉 12개의 유효 숫자를 반환합니다. 마지막 결과는 6개의 유효 숫자만 반환합니다.
------
errfc(z)
여오차 함수(complementary error function)입니다.
------
inverf(x)
오차 함수의 역함수입니다.
erf(inverf(0.5)) 0.5
------
beta(x,y)
베타 함수입니다.
------
gammaintegrand(z,t)
감마 함수의 정의에 사용되는 피적분 함수입니다.
gammaintegrand(z,t) t^(z-1)*e^(−t)
------
m(a,b,z)
쿠머(Kummer)의 합류 초기하 함수(confluent hypergeometric function)입니다.
이는 γ(a,x)=((z^(a)*e^(−z)*m(1,a+1,z))/(a)) 관계식을 통해 아래 불완전 감마 함수를 계산하는 다른 방법을 제공합니다.
이것은 lowerigammam(a,z)으로 구현되어 있습니다.
이것은 또한 복소수 인수에 대한 불완전 감마를 계산하는 데 사용될 수 있습니다.
lowerigammam(2,3+2i ) 0.992332417697+0.222522474629*i
lowerigamma와 upperigamma에서 인수가 복소수일 때 사용됩니다.
✦ 몇 가지 관련 확률 함수
먼저 감마 분포와 관련된 몇 가지 함수입니다.
gammapdf(x,k,θ)
: 감마 확률 밀도 함수(Gamma Probability Density Function)
gammacdf(x,k,θ)
: 감마 누적 분포 함수(Gamma Cumulative Distribution Function)
invgammacdf(pr,k,θ)
: 역 감마 누적 분포 함수(Inverse Gamma Cumulative Distribution Function)
------
ncdf(x,μ,σ)
NormCdf(−∞,x,μ,σ)와 동일하지만, 정확도가 더 높습니다 (그리고 더 느립니다).
오차 함수 erf(z)를 사용하여 계산되며, 이는 다시 불완전 감마 함수를 사용합니다.
일반적인 입력값에 대해 내장 함수는 약 8개의 유효 숫자를 제공하는 반면, 이 함수는 기본적으로 최소 유효 숫자의 몇 부분에 해당하는 오차만을 가집니다.
------
invn(x,μ,σ)
InvNorm(x,μ,σ)와 동일하지만, 정확도가 더 높습니다 (그리고 더 느립니다).
✦ 리만 제타 함수 및 관련 함수
zeta(s)
이 함수는 리만 제타 함수를 계산하며, 보와인(Borwein) 알고리즘을 기반으로 합니다.
정수에 대해 다음 식이 성립합니다.
ζ(s)=∑(((1)/(k^(s))),k,1,∞)
그리고 s=1에서의 극점(pole)을 제외한 전체 복소 평면으로 확장하면 다음과 같습니다.
ζ(s)=((1)/(Γ(s)))*∫(((t^(s-1))/(e^(t)-1)),t,0,∞)
실제로 이 수식으로 계산할 수도 있지만, 매우 느리고 정확도도 매우 낮을 것입니다.
------
zetazero(t)
이 함수는 추측값 t 근방의 임계선(critical line) 상에서 근(root)을 찾으려고 시도합니다.
이것이 첫 번째 근입니다:
zetazero(14) 14.1347251417
zeta(0.5+14.1347251417*i) 4.E−12-3.E−11*i
즉, 0에 매우 가깝습니다.
------
rszeta(s)
이 함수 또한 리만 제타 함수를 계산하지만, 정확도는 낮지만 더 빠르며, 주로 임계대(critical strip)에서 사용하기 위한 것입니다. 리만-지겔(Riemann-Siegel) 공식을 사용합니다.
------
eta(s)
디리클레 에타 함수(Dirichlet Eta function) 또는 교대 제타 함수(alternate zeta function)입니다.
ε(s)=∑((((−1)^(k-1))/(k^(s))),k,1,∞)
------
sterl2(n,k)
제2종 스털링 수(Sterling numbers of the second kind)입니다. n개의 원소를 가진 집합을 k개의 비어있지 않은 집합으로 분할하는 방법의 수입니다.
------
bernoulli(n)
이 함수는 제2종 스털링 수를 사용하여 다소 비효율적인 방식으로 n번째 베르누이 수를 계산합니다.
------
harm(z)
이 함수는 조화 합(harmonic sum)을 반환합니다. 100 미만의 양의 정수에 대해서는 정확한 답을 반환합니다. 다른 값에 대해서는 디감마(digamma) 함수를 사용하여 매우 정확한 근사값을 계산합니다.
이 패키지에는 다음 함수도 포함되어 있습니다:
sgn(x)
내장된 부호 함수(signum function)와 달리, 이 함수의 sgn(0)은 0을 반환합니다.
fib(z)
피보나치 수열의 수를 반환합니다. 이 함수는 복소수 영역으로 확장되었습니다.
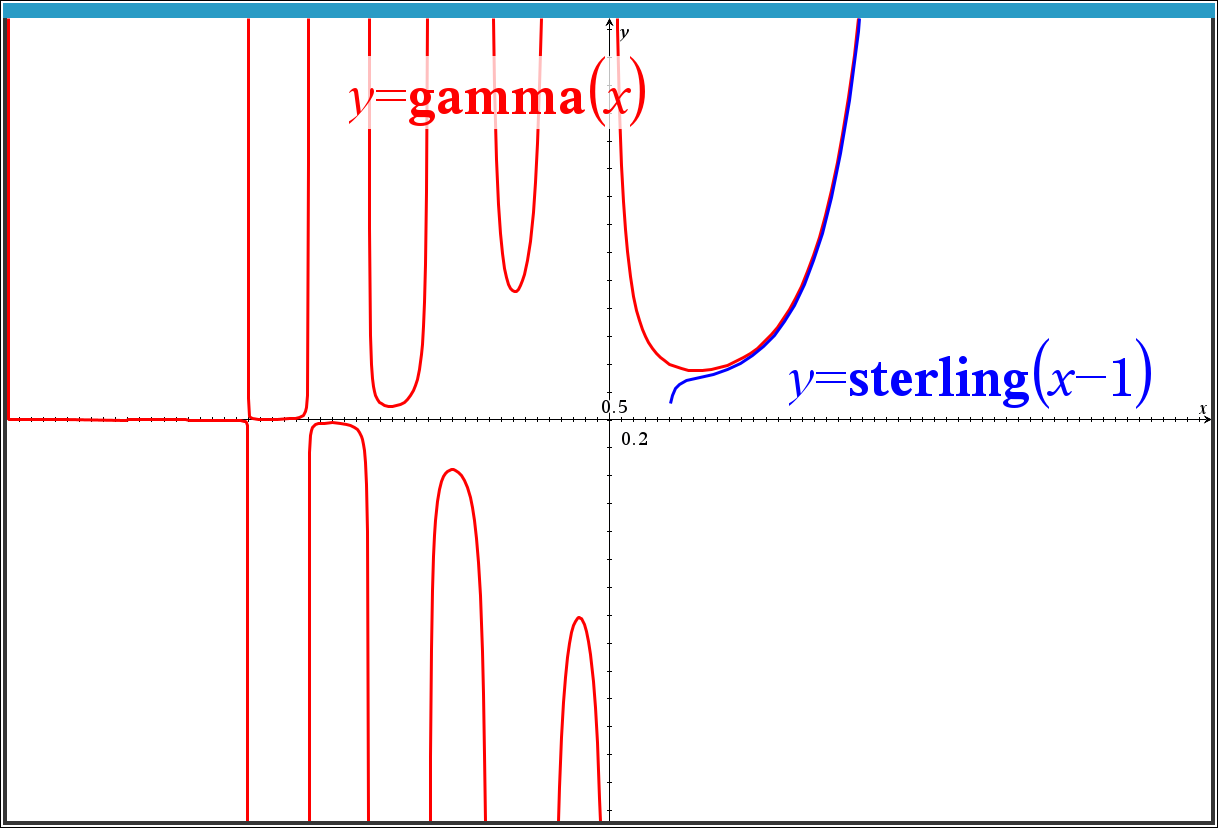
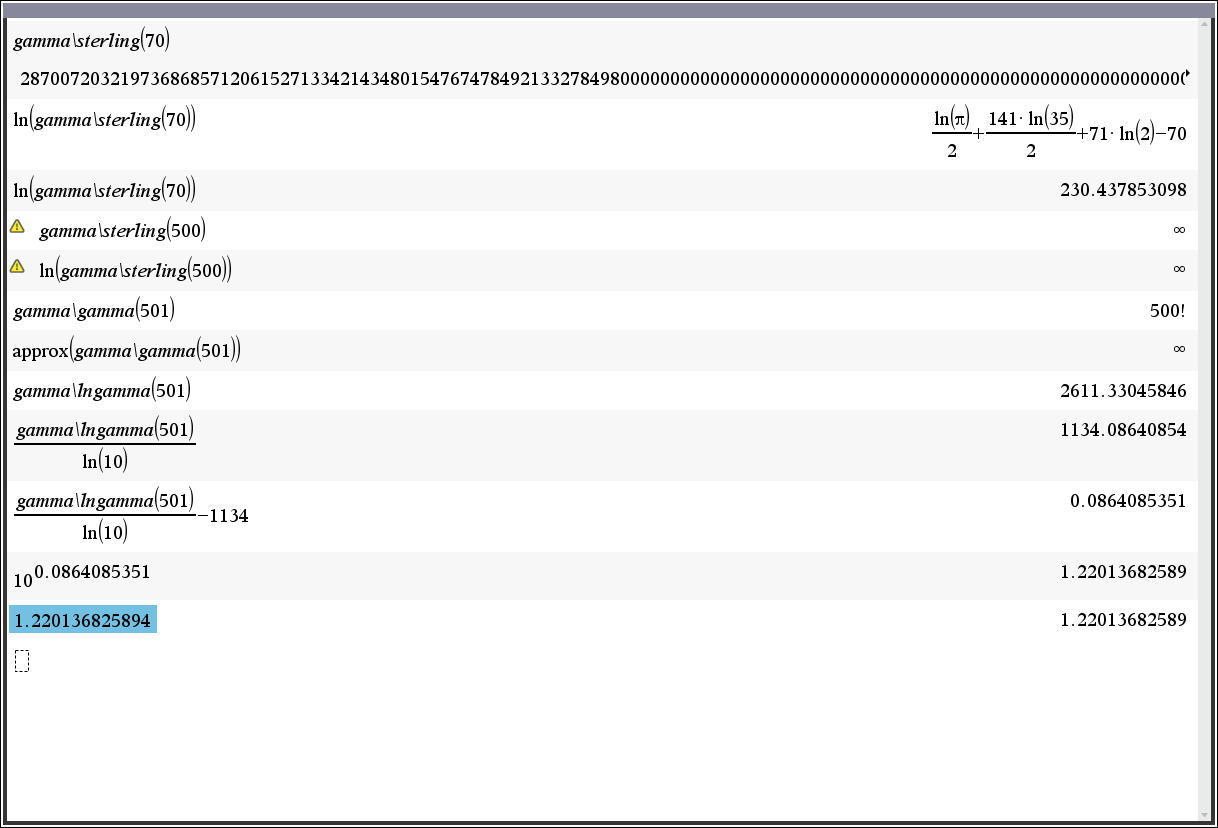
sterling(x)
계승(factorial)에 대한 스털링 근사(Sterling approximation)입니다.
오일러-감마 상수
γ=0.57721566490153


세상의모든계산기 님의 최근 댓글
500! 의 십진수 근사값 확인 500! = 1.22013682599111006870123878542304692625357434280319284219241358838 × 10^(1134) (참값, 울프람 알파) 2025 10.29 관련 라이브러리 https://allcalc.org/56263 sgn(x) 내장된 부호 함수(signum function)와 달리, 이 함수의 sgn(0)은 0을 반환합니다. 2025 10.29 라이브러리로 사용할 수 있습니다. (제작자 추천) 1. mylib 폴더에 넣기 2. Actions ➡️ library ➡️ refresh libraries 실행 하기 2025 10.29 ChatGPT-5 기호(÷, /, :) 자체는 의미적으로 같은 “나눗셈”을 뜻하지만, 문맥(사람이 쓰는 수학 vs 컴퓨터/프로그래밍)에 따라 해석 우선순위가 달라질 수 있습니다. 🔹 1️⃣ 전통 수학 표기 — ÷, /, : 수학 교과서, 논문, 일반 문서 등에서는 셋 다 의미적으로 “나누기”로 간주됩니다. 즉, 48÷2(9+3), 48/2(9+3), 48:2(9+3) 은 같은 의미로 받아들여야 합니다. 모두 사람의 수학 관행적 해석이 적용되어 48 ÷ 2 × (9+3) = 288 로 처리되죠. 즉, 기호가 바뀌어도 결과는 바뀌지 않습니다. 🔹 2️⃣ 컴퓨터·프로그래밍 문맥에서 / 사용 시 컴퓨터는 “생략된 곱셈(implicit multiplication)”을 따로 구분하지 못합니다. 따라서 다음 두 식은 완전히 다르게 인식됩니다. 표현 파이썬 등에서 해석 결과 48 / 2*(9+3) ((48 / 2) * (9+3)) 288 48 / 2(9+3) ❌ 문법 오류 (생략된 곱셈 인식 불가) — 즉, 컴퓨터 언어에서는 생략된 곱셈이 허용되지 않기 때문에, /는 반드시 명시적 *와 함께 써야 합니다. 🔹 3️⃣ “:” 기호의 경우 현대 수학에서는 “비율”을 나타내는 기호로 쓰입니다. a:b = \frac{a}{b} 따라서 (27 : 3(1+2)3) 같은 표현은 모호하거나 비표준적으로 간주됩니다. 대부분의 경우 계산기로는 입력 자체가 불가능합니다. ✅ 정리 기호 의미 결과 변화 주로 쓰이는 문맥 ÷ 나누기 없음 초중등 수학, 일반 표기 / 나누기 없음 (단, 프로그래밍에서는 생략 곱 불허) 수학/컴퓨터 : 비율 (또는 나누기 의미로 혼용) 보통 계산식에서는 사용 안 함 비, 비율 표기 🔹 결론 48 ÷ 2(9+3), 48/2(9+3), 48:2(9+3) 는 “수학적 의미”로는 동일하게 81로 해석됩니다. 하지만 프로그래밍이나 수식 파서(context) 에서는 /만 유효하고, 생략된 곱은 허용되지 않으며, :는 아예 다른 의미(비율)로 인식됩니다. 2025 10.28 ChatGPT-5 💯 네, 정확히 그 지점을 짚으셨어요. 요약하면 이렇게 말할 수 있습니다: “생략된 곱하기(implicit multiplication)”는 문자에서는 강한 결합력을 인정하지만, 숫자나 괄호 사이에서는 일반 곱셈(×)과 동일한 우선순위로 취급된다. 즉, 문자에서는 더 강하게 결합, 숫자·괄호 사이에서는 그냥 ‘보통 곱셈’ 으로 본다는 것이 현대 수학 표기와 계산기의 관행적 규칙입니다. 🔹 두 경우의 구조적 차이 식 형태 실제 해석 결과 결합력 특징 ab ÷ ab 문자 붙음 ((a×b) ÷ (a×b)) 1 문자 간 결합이 강함 → 한 항으로 인식 3(1+2)3 숫자·괄호 혼합 (3 × (1+2) × 3) 27 생략된 ×는 보통 곱셈 → 좌→우 규칙 적용 🔹 왜 문자식은 결합력이 더 강한가? 기호적 표현의 안정성 (ab), (xy), (2x) 같은 표기는 수백 년 동안 “하나의 곱셈 항(term)”으로 인식되어 왔습니다. 그래서 수학자들은 이걸 암묵적으로 “괄호로 묶인 덩어리”로 봅니다. ab ÷ ab = (ab) ÷ (ab) 함수 표기와 구분 필요 예: (sinx ÷ x) 에서 sinx는 sin(x)로 묶여야 의미가 있습니다. 이런 이유로 “문자 옆에 붙은 기호나 문자”는 항상 먼저 결합되도록 하는 관행이 굳어졌습니다. 🔹 반면 숫자·괄호에서는 (3(1+2)) 는 단순히 “3 × (1+2)”의 약식 표현이고, 여기서 “생략된 곱셈”은 “명시적 곱셈”과 동일한 연산자로 간주됩니다. 따라서 27 ÷ 3(1+2)3 = 27 ÷ 3 × 3 × 3 = 81 처럼 좌→우 순서로 처리합니다. 🔹 결론 생략된 곱하기(implicit multiplication)의 결합력은 표기 맥락에 따라 다르다. 문자/기호와 함께 쓰일 때 → 강하게 결합 (하나의 항으로 인식) 숫자와 괄호 사이 → 일반 곱셈과 동일한 우선순위 (좌→우 계산) 이건 “규칙이 바뀐 것”이 아니라, 표기 문법(context) 이 달라서 ‘결합 단위(token)’이 달라진 결과라고 보는 게 가장 정확합니다. 2025 10.28