- TI nspire
[TI-nspire] 아랫첨자(Subscript)를 사용하여 문자열 생성하기
1. 템플릿(Template) 이용

- 위 템플릿을 이용하면 아랫첨자를 쉽게 입력할 수 있습니다.
- 숫자 나 문자를 아래첨자에 입력할 수 있습니다.
- 아랫첨자를 연속으로 입력하는 것도 가능합니다.
- 아랫첨자에 들어가는 내용은 모두 문자열(String) 처리되므로 수식계산(Expr) 방식으로 입력할 수는 없습니다.
2. 카탈로그(Catalog) 이용
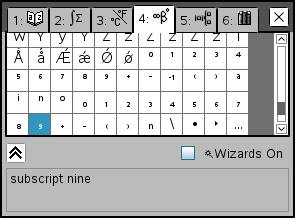
- 카탈로그(Catalog) 의 문자표에서 아랫첨자에 해당하는 문자를 찾아서 하나씩 입력할 수도 있습니다.
- 다만, (TI-nspire에서 사용 가능한) 모든 아랫 첨자 문자가 Catalog 에 제시되는 것은 아닙니다.
3. char() 함수 이용
- 아랫첨자인 문자에 대응하는 숫자를 이용해 char(int) 형식으로 입력할 수 있습니다.
- 아랫첨자 숫자 0~9 는 차례대로 8320~8329 까지 입니다.

- 아랫첨자 알파벳 대문자 A~Z 는 차례대로 63553~63578 까지입니다.
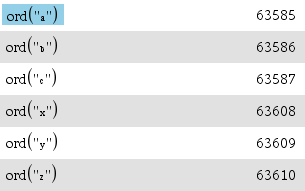
- 아랫첨자 알파벳 소문자 a~z 는 차례대로 63585~63610 까지입니다.
- 아랫첨자(subscript)를 이용해 index를 자동생성하려면 &char(8320) 과 같은 방식으로 한글자씩 따로따로 문자열 처리하여야 합니다. (더 좋은 방법이 있을 것도 같습니다만, 저는 아직 찾지 못하였습니다. 찾으시면 제보 바랍니다.)
:Define indexsub()= :Prgm :Local idstr,idn,i,j :Request "How many index?",n,0 :For i,1,n : idstr:="" : idn:=i : For j,1,int(log(i,10))+1 : char(8320+expr(right(string(idn),1)))&idstr→idstr : int(((idn)/(10)))→idn : EndFor :"i"&idstr→idstr : DispAt 1,idstr,"=",i :EndFor :EndPrgm
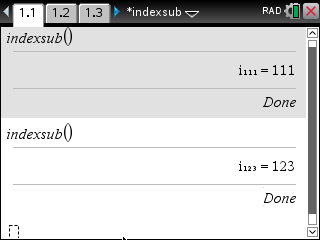
- 아랫첨자는 변수명에 사용할 수도 있습니다.
- 아랫첨자는 변수명/인덱스명으로 사용할 때 단순히 보기에 좋을 뿐, 특별한 효과는 없습니다.
추천인


 탱글탱글
탱글탱글
세상의모든계산기 님의 최근 댓글
참고 : 라플라스 해법 1- 문제풀이의 개요 [출처] 라플라스 해법 1- 문제풀이의 개요|작성자 공학 엔지니어 지망생 https://blog.naver.com/hgengineer/220380176222 2026 01.01 3×3 이상인 행렬의 행렬식 determinant https://allcalc.org/50536 2025 12.30 답에 이상한 숫자 14.2857142857가 들어간 것은 조건식에 소숫점(.) 이 들어가 있기 때문에 발생한 현상이구요. 100÷7 = 14.285714285714285714285714285714 소숫점 없이 분수로 식이 주어졌을 때와 결과적으로는 동일합니다. 2025 12.30 그럼 해가 무한히 많은지 아닌지 어떻게 아느냐? 고등학교 수학 교과과정에 나오는 행렬의 판별식(d, determinant)을 이용하면 알 수 있습니다. ㄴ 고교과정에서는 2x2 행렬만 다루던가요? 연립방정식의 계수들로 행렬을 만들고 그 행렬식(determinant)을 계산하여야 합니다. 행렬식이 d≠0 이면 유일한 해가 존재하고, d=0 이면 해가 없거나 무수히 많습니다. * 정상적인 경우 (`2y + 8z = 115`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 8 | 행렬식 값 = 1(0 - (-7)) - 1(8 - 0) = 7 - 8 = -1 (0이 아니므로 유일한 해 존재) * 문제가 된 경우 (`2y + 7z = 100`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 7 | 행렬식 값 = 1(0 - (-7)) - 1(7 - 0) = 7 - 7 = 0 (0이므로 유일한 해가 존재하지 않음) 2025 12.30 좀 더 수학적으로 말씀드리면 (AI Gemini 참고) 수학적 핵심 원리: 선형 독립성(Linear Independence) 3원 1차 연립방정식에서 미지수 x, y, z에 대한 단 하나의 해(a unique solution)가 존재하기 위한 필수 조건은 '주어진 세 개의 방정식이 서로 선형 독립(linearly independent) 관계에 있어야 한다'는 것입니다. * 선형 독립 (Linearly Independent): 어떤 방정식도 다른 방정식들의 조합(상수배를 더하거나 빼는 등)으로 만들어질 수 없는 상태입니다. 기하학적으로 이는 3개의 평면(각 방정식은 3D 공간의 평면을 나타냄)이 단 한 개의 점(해)에서 만나는 것을 의미합니다. * 선형 종속 (Linearly Dependent): 하나 이상의 방정식이 다른 방정식들의 조합으로 표현될 수 있는 상태입니다. 이 경우, 새로운 정보를 제공하지 못하는 '잉여' 방정식이 존재하는 것입니다. 기하학적으로 이는 3개의 평면이 하나의 선에서 만나거나(무수히 많은 해), 완전히 겹치거나, 혹은 평행하여 만나지 않는(해가 없음) 상태를 의미합니다. 질문자님의 사례는 '선형 종속'이 되어 무수히 많은 해가 발생하는 경우입니다. 2025 12.30