- TI nspire
[TI-nspire] ÉTS 에서 만든 TI-Nspire 용 라이브러리 (Geo3D)
-
- 2024.09.05 - 10:05 2015.11.05 - 11:31 1010 3
École de technologie supérieure (ÉTS)
ÉTS 는 캐나다 퀘벡주 몬트리올에 위치한 공과대학입니다.
ETS는 특히 응용 과학과 공학 분야에 중점을 두며, 산업과 밀접한 관계를 유지하면서 실용적인 기술 교육을 제공합니다.
이 학교는 주로 기술자들이나 공학 관련 직업을 목표로 하는 학생들을 위해 설계된 프로그램을 제공하며, 연구와 개발에도 적극적으로 참여하고 있습니다.
ETS는 다양한 공학 분야에서 학사, 석사, 박사 학위를 제공하며, 특히 실무 중심의 교육 방식을 통해 학생들이 현장에서 바로 활용할 수 있는 기술과 지식을 습득할 수 있도록 돕습니다.
http://seg-apps.etsmtl.ca/nspire/librairies.html
위 링크 들어가 보시면 총 4개의 라이브러리 파일이 있습니다.
잘은 모르지만,
모르는 사람이 봐도 상당히 공들여 만든 라이브러리로 보여집니다.
1. De Michel Beaudin, une librairie de fonctions et procédures utiles pour les cours MAT-144-145-165-265-472-805 et MEC-532.
2. Librairie geo3d : geo3d.tns (18 juillet 2014)
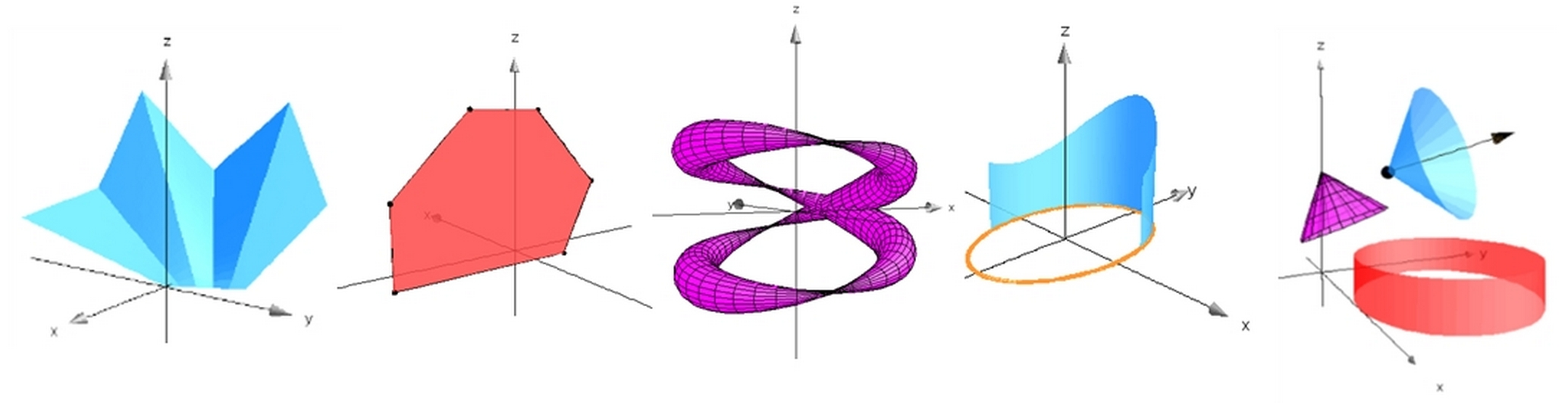
3. Library geo3d in ENGLISH : geo3d.tns (25 juin 2014)
4. Librairie signum : signum.tns (25 juin 2014)
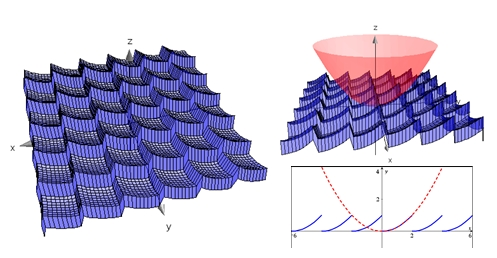
2번 3번은 같은 라이브러리인데 언어만 다른 것으로 파악됩니다만,
2번의 경우 날짜가 좀 다른데, 2018년에 추가로 업데이트가 있었던 것 같기도 하고, 아닌 것 같기도 하고 그렇네요.
geo3d 라이브러리 목록에는 아래 함수들이 들어 있습니다.
-
25
댓글3
-
세상의모든계산기
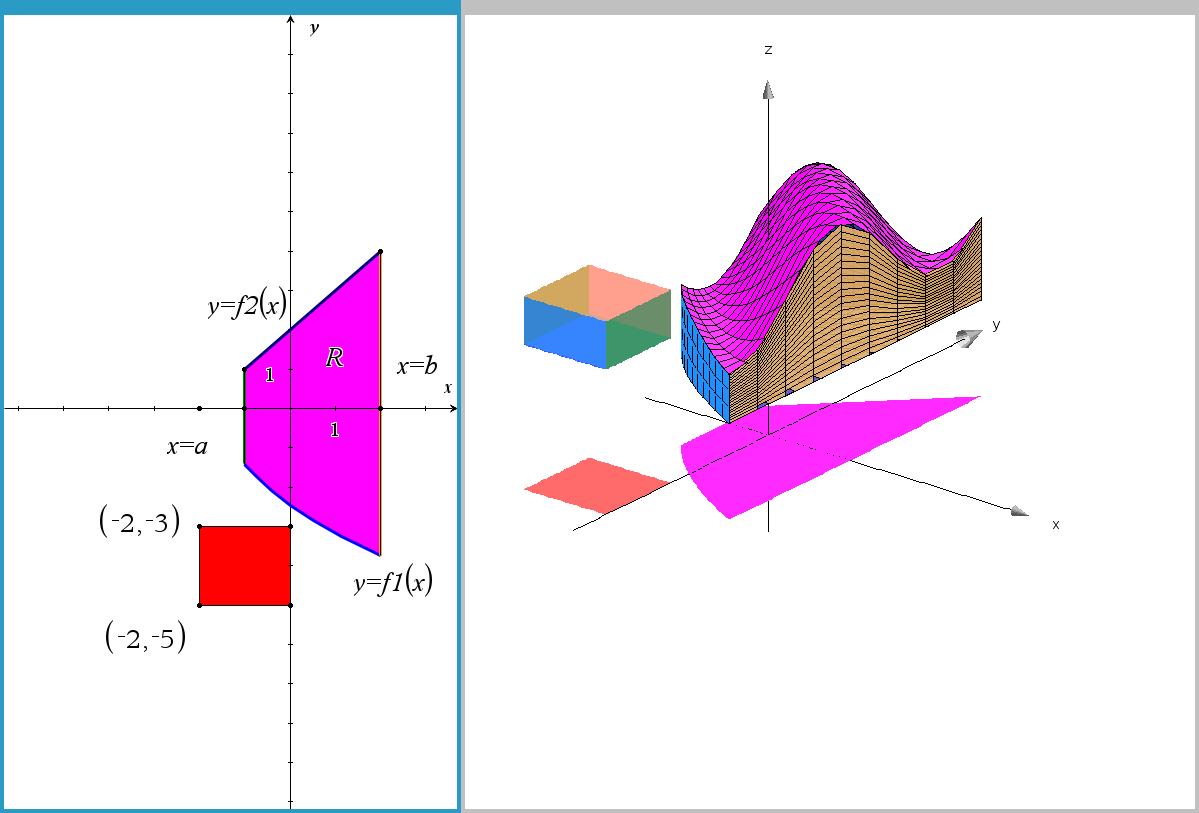
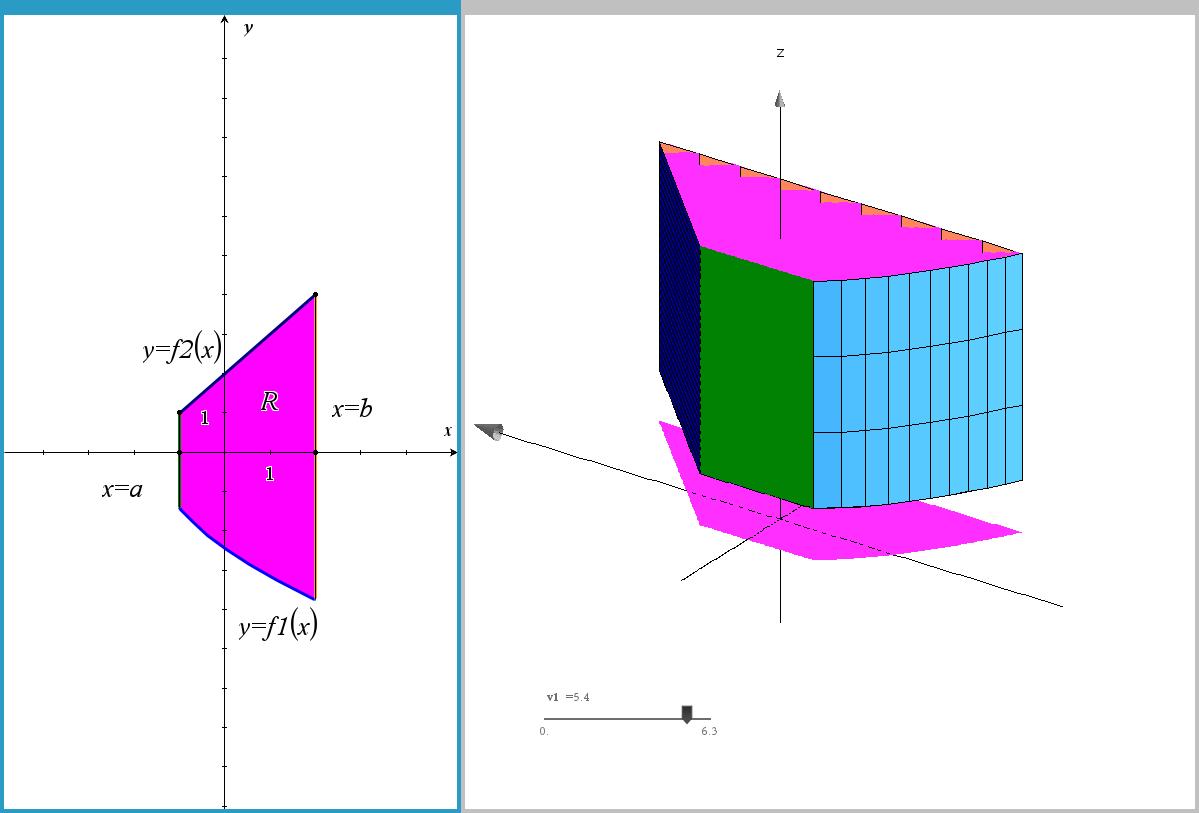
샘플 파일 TracerSolides.tns 예제 일부 (18 juillet 2018).
-
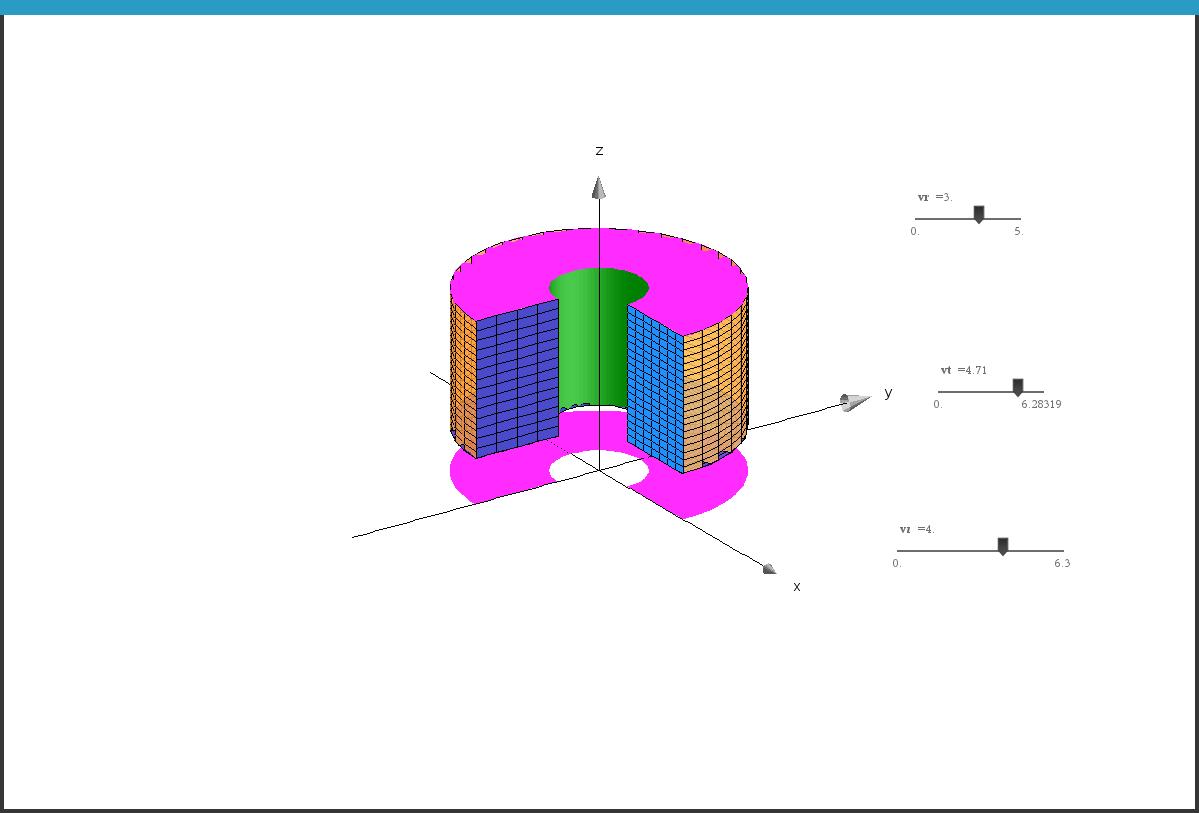
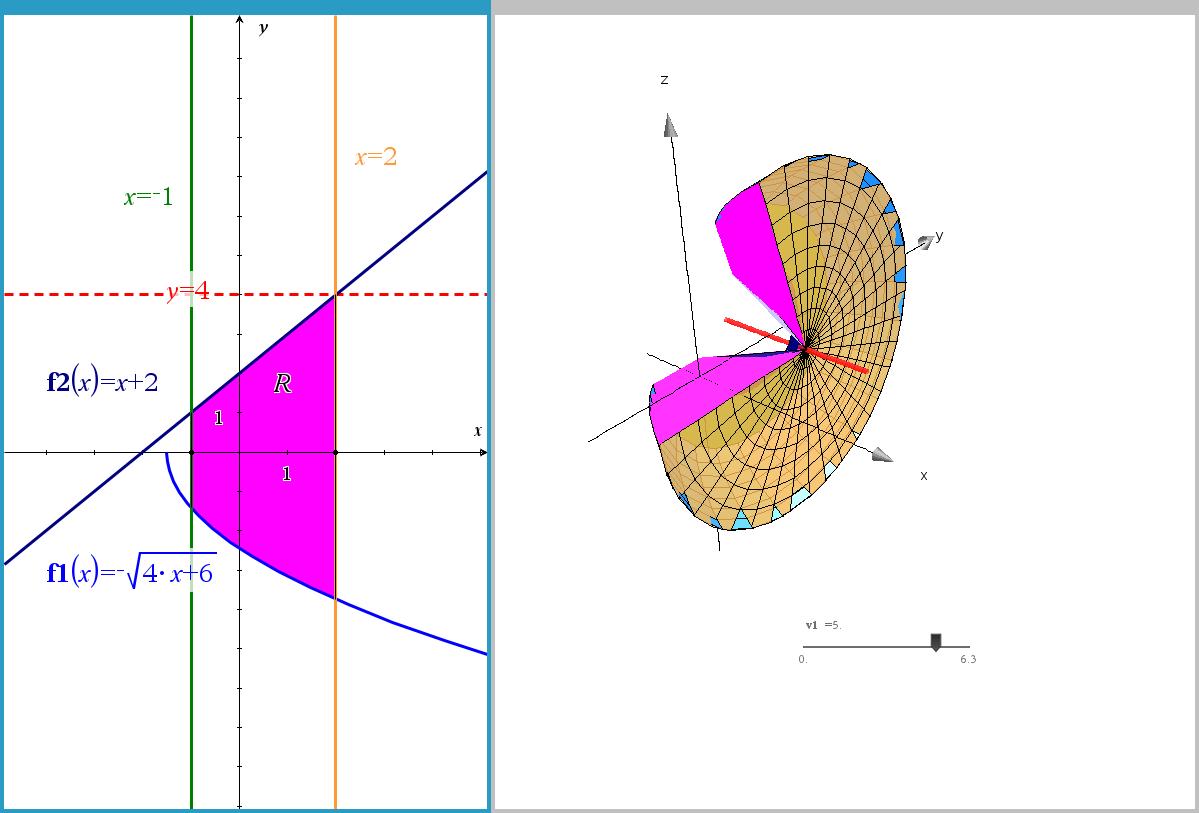
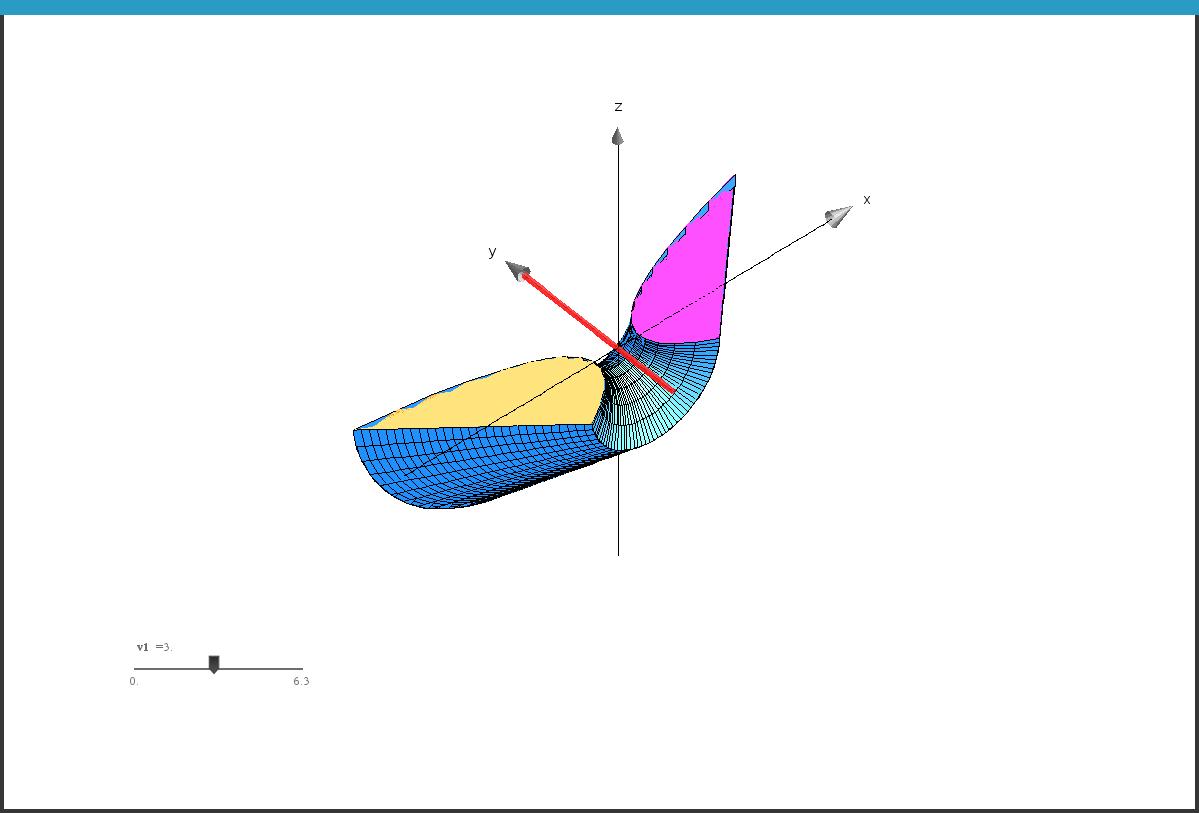
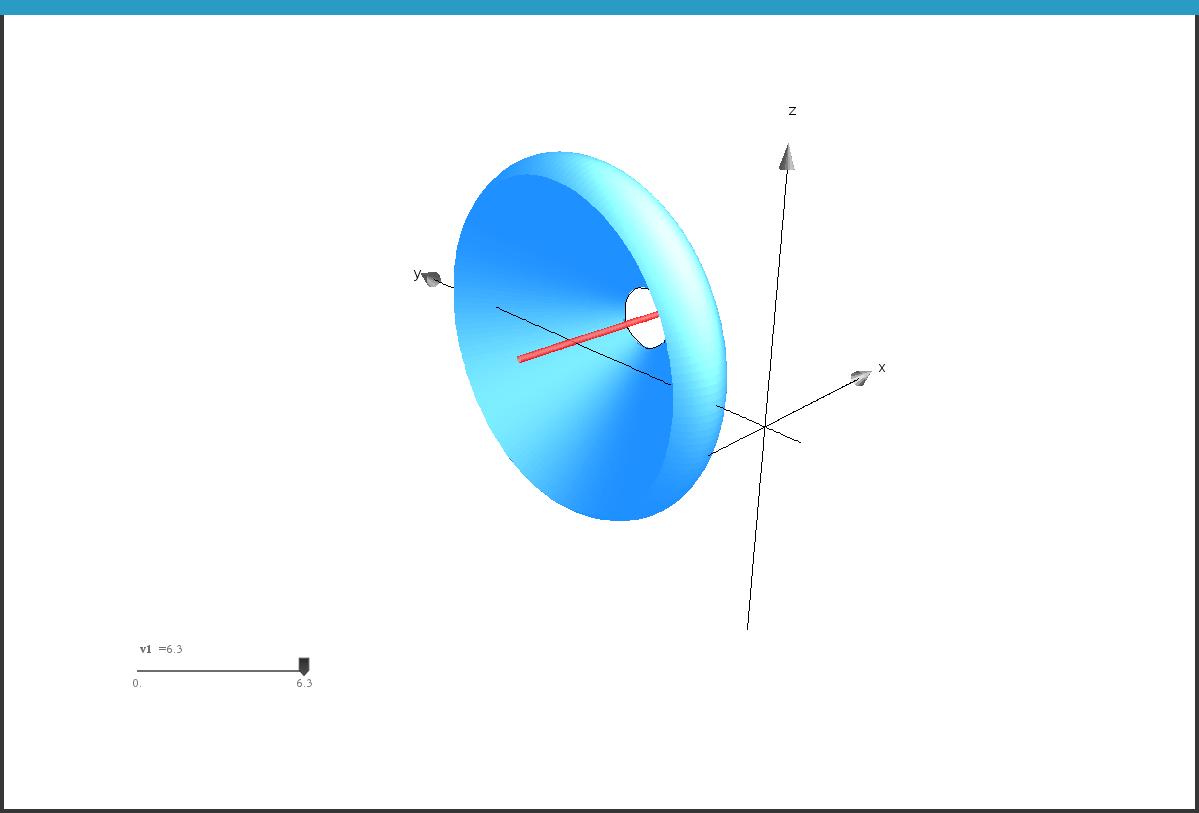
세상의모든계산기
x=1, y=1, z=1 평면 그리기 - geo3d\polygon()
1. z=1 은 function 타입으로 입력합니다. z1(x,y) = 1
2. y=1, z=1 은 function 타입으로 입력할 방법이 없습니다.
플롯할 범위를 먼저 생각하고 꼭지점을 구합니다.
폴리곤은 삼각형 단위로 면을 채우는 기능이므로 사각형 평면을 만들려면 2개의 폴리곤이 각각 필요합니다.
ㄴ 점의 순서는 그렇게 중요하진 않은데, 추가적으로 이용을 하려면 중요할 수도 있겠습니다.
y1~y4 에 대해서도 같은 방식으로 처리를 한 다음에 g3, g4에 저장.
geo3d\putg(1,4) 를 실행하면 g1~g4에 대한 처리가 끝납니다.
그래프 페이지로 넘어가서, 해당 함수를 활성화하면 그래프가 표시됩니다.
ㄴ z=1은 하나의 색, x=1, y=1 은 두개의 색(삼각형)으로 처리되었습니다.
ㄴ 티 안나게 하려면 색은 수동으로 변경 설정하셔야 합니다.
세상의모든계산기 님의 최근 댓글
[일반계산기] 매출액 / 원가 / 마진율(=이익율)의 계산. https://allcalc.org/20806 2026 02.08 V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04 1. 분모 먼저 계산 400 × 10000 = 100 × 6000 = GT 결과값 4,600,000 역수 처리 ÷÷== 결과값 0.00000021739 2. 분자 곱하기 ×3 00 00 00 ×4 00 ×1 00 00 최종 결과 = 2,608,695.65217 2026 02.04 해결 방법 1. t=-1 을 기준으로 그래프를 2개로 나누어 표현 ㄴ 근데 이것도 tstep을 맞추지 않으면 문제가 발생할 것기도 하고, 상관이 없을 것 같기도 하고... 모르겠네요. 2. t=-1 이 직접 계산되도록 tstep을 적절하게 조정 tstep=0.1 tstep=0.01 도 해 보고 싶지만, 구간 크기에 따라 최소 tstep 이 변하는지 여기서는 0.01로 설정해도 0.015로 바뀌어버립니다. 그래서 tstep=0.02 로 하는게 최대한 긴 그래프를 얻을 수 있습니다. 2026 02.02