- CASIO 570
[fx-570 ES PLUS] VECTOR Calculation 벡터 계산
1. 벡터 계산 모드


2. 기능 설명 (Manual 참고)



3. 예시 (Manual 참고)

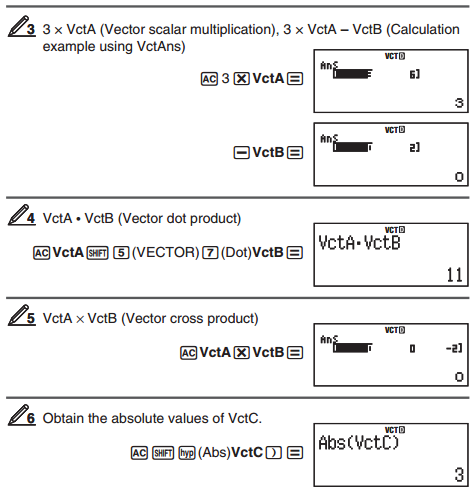
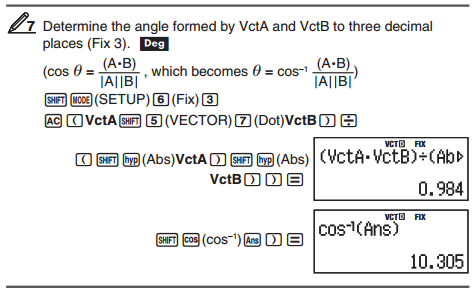
댓글5
-
1
세상의모든계산기
공학용 계산기 카시오 fx-570ES Plus를 사용하여 벡터 연산을 수행하는 방법을 안내해드리겠습니다.
문제는 벡터 \(\mathbf{v} = 2i - 2j + 4k\)를 크기로 나누는 것입니다.
벡터의 크기(노름)를 구하는 방법은 다음과 같습니다:
\[
|\mathbf{v}| = \sqrt{2^2 + (-2)^2 + 4^2} = \sqrt{4 + 4 + 16} = \sqrt{24} = 2\sqrt{6}
\]따라서 정규화된 벡터는:
\[
\frac{\mathbf{v}}{|\mathbf{v}|} = \frac{2i - 2j + 4k}{2\sqrt{6}} = \frac{2}{2\sqrt{6}}i - \frac{2}{2\sqrt{6}}j + \frac{4}{2\sqrt{6}}k = \frac{1}{\sqrt{6}}i - \frac{1}{\sqrt{6}}j + \frac{2}{\sqrt{6}}k
\]
- MODE 8
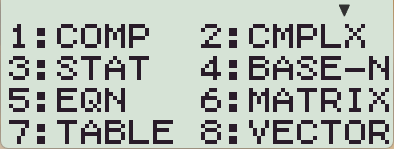
- 입력할 벡터 변수 선택 (1~3)
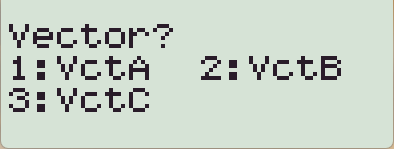
- 3차원 벡터이니 Dimension 을 3으로 선택
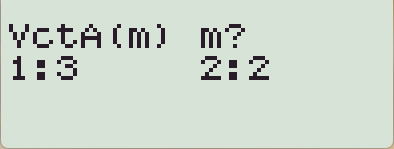
- 벡터 요소를 입력

- 벡터 입력이 끝났으면 AC 를 눌러 밖으로 빠져 나오고
SHIFT hyp 을 눌러 ABS( 명령을 띄움)
SHIFT 5 (Vector) 명령어 메뉴를 열고 아까 입력한 (VctA) 를 선택
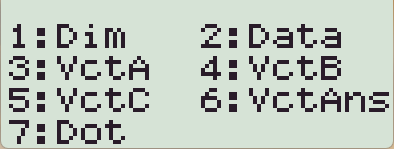
= 을 누르면 길이가 계산됨 (루트꼴로 표시 불가)
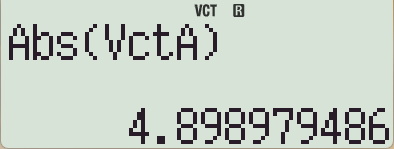
ㄴ 이 값은 Ans 에 저장됨.
- 다시
SHIFT 5 (Vector) 명령어 메뉴를 열고,
아까 입력한 VctA 를 선택하고,
÷ Ans 를 입력하고 = 계산
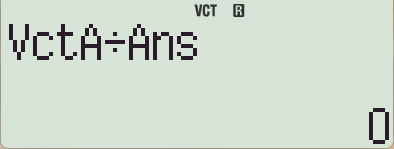
ㄴ 이 값은 Ans 가 아닌 VctAns 에 저장됨.
- 최종 결과가 Vector 형식으로 표현됨.
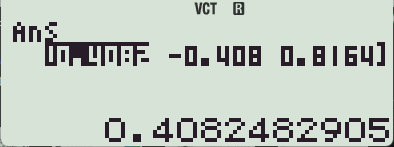
ㄴ 여기서도 숫자는 Decimal 형태로 나오고, 루트를 이용한 표현은 불가능합니다.
fx-570 시리즈 벡터 계산에서
루트를 포함한 결과를 얻고 싶으시면 하나씩 계산하셔야 합니다.
1. 분모의 크기를 계산합니다.
- 계산기에서 √(2^2 + 2^2 + 4^2)를 입력합니다.
- 이 계산 결과는 2√6입니다.
2. 각 성분을 분모로 나눕니다.
- 계산기에서 2 / (2√6)를 입력하여 i 성분을 계산합니다.
- 2를 입력하고 /를 누른 뒤, 괄호를 열고 2 * √6을 입력합니다. 계산 결과 1/√6이 나옵니다.
- 마찬가지로 -2 / (2√6)를 입력하여 j 성분을 계산합니다.
- -2를 입력하고 /를 누른 뒤, 괄호를 열고 2 * √6을 입력합니다. 계산 결과 -1/√6이 나옵니다.
- 마지막으로 4 / (2√6)를 입력하여 k 성분을 계산합니다.
- 4를 입력하고 /를 누른 뒤, 괄호를 열고 2 * √6을 입력합니다. 계산 결과 2/√6이 나옵니다.결과적으로, 각 성분을 나눈 값을 합하여 정규화된 벡터를 얻을 수 있습니다.
따라서 정규화된 벡터는:
\[
\frac{1}{\sqrt{6}}i - \frac{1}{\sqrt{6}}j + \frac{2}{\sqrt{6}}k
\]이 방법을 사용하여 공학용 계산기에서 벡터 연산을 수행할 수 있습니다.
- MODE 8
- 2
-
세상의모든계산기
예제 : 두 벡터 \( \mathbf{A} = 2\hat{i} + 4\hat{j} \)와 \( \mathbf{B} = 6\hat{j} - 4\hat{k} \) 사이의 각도 \( \theta \)를 구하시오.
두 벡터 사이의 각도 \( \theta \)는 벡터 내적(dot product)을 이용하여 다음과 같이 구할 수 있습니다.
벡터 내적 공식은 다음과 같습니다:
\[
\mathbf{A} \cdot \mathbf{B} = |\mathbf{A}| |\mathbf{B}| \cos \theta
\]
따라서 각도 \( \theta \)는 다음과 같이 구할 수 있습니다:
\[
\cos \theta = \frac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{A}| |\mathbf{B}|}
\]1. 벡터 내적 계산
\[
\mathbf{A} \cdot \mathbf{B} = (2\hat{i} + 4\hat{j}) \cdot (6\hat{j} - 4\hat{k})
\]
내적은 각 성분끼리의 곱만을 더합니다. 즉:
\[
\mathbf{A} \cdot \mathbf{B} = (2)\cdot(0) + (4)\cdot(6) + (0)\cdot(-4) = 24
\]2. 벡터 크기 계산
\begin{aligned}|\mathbf{A}| = \sqrt{2^2 + 4^2} = \sqrt{4 + 16} = \sqrt{20} = 4.47 \\
|\mathbf{B}| = \sqrt{6^2 + (-4)^2} = \sqrt{36 + 16} = \sqrt{52} = 7.21 \end{aligned}
3. 각도 \( \theta \) 계산
\[
\cos \theta = \frac{24}{4.47 \times 7.21} = \frac{24}{32.24} \approx 0.7445
\]
따라서:
\[
\theta = \cos^{-1}(0.7445) \approx 41.9^\circ
\]답
두 벡터 사이의 각도는 약 \( 41.9^\circ \)입니다. -
1
세상의모든계산기
[fx-570EX] 이용 계산
【MENU】【5】
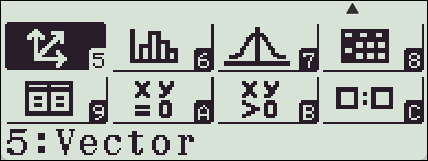
Define Vector A 【1】Dimension 【3】
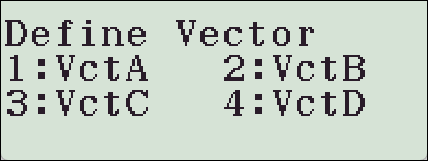
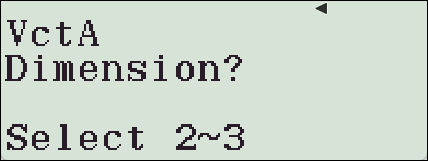

입력 후 【AC】로 Edit 모드 나오기
B도 같은 방식으로 입력
【OPTN】【4】

입력 후 【AC】로 Edit 모드 나오기
계산 버튼 입력 :
【SHIFT】【COS】【(】【OPTN】【3】【OPTN】【▼】【2】 : Dot Product

【OPTN】【4】【)】【÷】【(】【SHIFT】【(】【OPTN】【3】【)】【SHIFT】【(】【OPTN】【4】
【)】【)】【)】 마지막 닫는 괄호들은 생략 가능
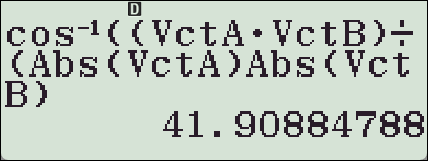
* 결과값(각도)이 다르다면 Degree / Radian 확인


세상의모든계산기 님의 최근 댓글
설명서 : https://www.casio.com/content/dam/casio/global/support/manuals/calculators/pdf/2022/f/fx-9910CW_EN.pdf 2026 01.02 참고 : 라플라스 해법 1- 문제풀이의 개요 [출처] 라플라스 해법 1- 문제풀이의 개요|작성자 공학 엔지니어 지망생 https://blog.naver.com/hgengineer/220380176222 2026 01.01 3×3 이상인 행렬의 행렬식 determinant https://allcalc.org/50536 2025 12.30 답에 이상한 숫자 14.2857142857가 들어간 것은 조건식에 소숫점(.) 이 들어가 있기 때문에 발생한 현상이구요. 100÷7 = 14.285714285714285714285714285714 소숫점 없이 분수로 식이 주어졌을 때와 결과적으로는 동일합니다. 2025 12.30 그럼 해가 무한히 많은지 아닌지 어떻게 아느냐? 고등학교 수학 교과과정에 나오는 행렬의 판별식(d, determinant)을 이용하면 알 수 있습니다. ㄴ 고교과정에서는 2x2 행렬만 다루던가요? 연립방정식의 계수들로 행렬을 만들고 그 행렬식(determinant)을 계산하여야 합니다. 행렬식이 d≠0 이면 유일한 해가 존재하고, d=0 이면 해가 없거나 무수히 많습니다. * 정상적인 경우 (`2y + 8z = 115`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 8 | 행렬식 값 = 1(0 - (-7)) - 1(8 - 0) = 7 - 8 = -1 (0이 아니므로 유일한 해 존재) * 문제가 된 경우 (`2y + 7z = 100`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 7 | 행렬식 값 = 1(0 - (-7)) - 1(7 - 0) = 7 - 7 = 0 (0이므로 유일한 해가 존재하지 않음) 2025 12.30