- CASIO 350
[fx-350] 2차 방정식 해를 찾는 방법 - 2차 회귀식
-
- 2024.10.20 - 18:13 2015.10.22 - 23:31 31469 3
1. [fx-350] 시리즈의 한계
[fx-350] 기종은 EQN 모드도 없고, Solve 기능도 없기 때문에 일반적인 방법으로는 방정식의 해를 구할 수가 없습니다.
* 동급인 fx-82도 같습니다만, fx-95 시리즈에는 EQN기능이 들어가 있습니다.
https://support.casio.com/global/ko/calc/manual/fx-82ESPLUS_85ESPLUS_95ESPLUS_350ESPLUS_ko/using_calculation_modes/equation_calculations.html
2. 2차 방정식의 해 - 근의 공식 (fx-350 시리즈에서는 이 방법이 최선입니다)
그럼에도 불구하고... 2차 방정식의 해를 찾아야만 한다면? 근의 공식을 이용하는 수밖에 없습니다.
$$ x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} $$
기억이 가물가물 한데... 근의 공식을 중1 수학시간에 배웠던가???
산수에서 수학으로 넘어가는 첫번째 관문이라고 할 수가 있죠.
그나마도 ± 기호를 넣을 수 없으니, 식을 두번 따로 따로 계산해야 합니다.
예시) -4.905t^2+10t+20=0 의 해를 구해봅시다.
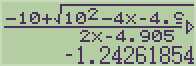
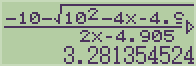
3. 2차 방정식의 해 - 편법 (2차 회귀식 Regression)
하지만, 이 계산기에도 기본 통계 기능은 있고, 나름 회귀 방정식이라는 것도 구할 수가 있습니다.
그렇습니다. 나름 방정식입니다. 우리가 찾는 바로 그 방정식과 같은 이름입니다. 선형 회귀, 지수회귀, 로그회귀, 그리고 다항식(2차) 회귀 등을 구할 길이 작게 열렸습니다.
한번 해 볼까요?
- 통계 모드로 들어갑니다. 【MODE】【2】 STAT
(계산기 모델에 따라서 메뉴번호가 조금 다를 수도 있습니다.)
- 암호같은 기호들이 잔뜩 나타나는데 당황하지 말고,
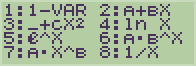
X의 제곱(²)기호가 있는 【3】_+cX² 을 선택
- 빈 칸이 나타났다면
빈칸의 X와 Y에 방정식이 지나는 {X,Y} 순서쌍을 딱 3개만 넣어줍니다.
지금은 방정식 : -4.905t^2+10t+20=0 의 해를 구하고 있기 때문에 최대한 간단한 것을 찾아 넣습니다.
(암산으로도 구할 수 있는) 좌표 {0,ㅁ} {1,ㅁ} {-1,ㅁ} 을 입력합니다. 어차피 계산기로 계산해서 넣으면 되니까 부담갖지 마시구요.
- X부터 차례대로
【0】【=】
【1】【=】
【(-)】【1】【=】
Y는 차례대로
【20】【=】
【-4.905*(1)+10*(1) +20】【=】
【-4.905*(1)+10*(-1)+20】【=】
- DATA 입력이 끝났으면 【AC】를 눌러서 밖으로 나옵니다.
- 【SHIFT】 【1】 을 눌러서 STAT 관련 화면을 띄웁니다.
ㄴ [fx-350EX] 기종은 【OPTN】 으로 들어가서 찾아보세요.
- 【7】 : Reg 을 선택합니다. 회귀 변수들이 보입니다.
A, B, C는 입력한 DATA(쌍)로부터 구해진 2차 회귀식(=방정식)의 계수들입니다.
x(햇)은 x절편, y(햇)은 y절편을 찾을 때 사용합니다.
- 【4】 : x(햇=모자)1 또는 【5】 : x(햇=모자)2 을 눌러서 변수를 불러냅니다.
그리고 그 앞에! 0을 붙이고 【=】를 누르면 신기하게도 근이 구해집니다.
ㄴ y=0에 해당하는 x절편 2개를 의미합니다. 즉 방정식=0 을 만족하는 두 해가 찾아진 것입니다.
ㄴ 찾아진 절편값은 변수 메모리에 바로 저장(STO)할 수도 있고,
앞 뒤로 괄호를 쳐서 결과값을 가공할 수도 있습니다.
(괄호 안쳐도 되긴 합니다만, 모양상 치는 편이 헷갈리지 않을 듯)
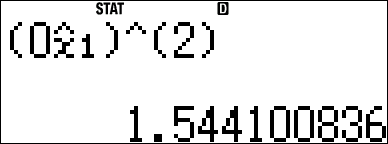
근의 공식보다도 많이 복잡해 보이지만, 여튼 구하는 방법이 있다는 데 의의를...
위에서 y=0 과 방정식이 만나는 점인 해(y=0에서의 x절편)를 찾았다면, y=1 일 때의 x절편도 찾을 수 있습니다.
그래프로 표현하면 이렇게 됩니다.
[fx-350MS] 기종도 (키 입력방법은 다르지만) 같은 원리로 해를 구할 수 있습니다.
-
25
세상의모든계산기 님의 최근 댓글
엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10 엑셀 / 행의 최대 개수, 열의 최대 개수, 셀의 최대 개수 엑셀의 행 개수 제한은 파일 형식에 따라 다르며, 최신 .xlsx 파일 형식은 시트당 최대 1,048,576행까지 지원하지만, 구형 .xls 파일은 65,536행으로 제한됩니다. 따라서 대용량 데이터를 다룰 때는 반드시 최신 파일 형식(.)으로 저장해야 하며, 행과 열의 총 수는 1,048,576행 x 16,384열이 최대입니다. 주요 행 개수 제한 사항: 최신 파일 형식 (.xlsx, .xlsm, .xlsb 등): 시트당 1,048,576행 (2^20). 구형 파일 형식 (.xls): 시트당 65,536행 (2^16). 그 외 알아두면 좋은 점: 최대 행 수: 1,048,576행 (100만여개) 최대 열 수: 16,384열 (XFD) 대용량 데이터 처리: 65,536행을 초과하는 데이터를 다루려면 반드시 .xlsx 형식으로 저장하고 사용해야 합니다. 문제 해결: 데이터가 많아 엑셀이 멈추거나 오류가 발생하면, 불필요한 빈 행을 정리하거나 Inquire 추가 기능을 활용하여 파일을 최적화할 수 있습니다. 2026 02.10 [일반계산기] 매출액 / 원가 / 마진율(=이익율)의 계산. https://allcalc.org/20806 2026 02.08 V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04