- TI nspire
[TI-nspire] (프로그램) 보간법 (선형, 다항식) Linear & Polynomial Interpolation
-
- 2024.06.26 - 09:44 2015.01.15 - 22:05 6672 10
Linear & Polynomial Interpolation for TI-Nspire
Ver 1.2
by allcalc.org
-----
Usage
1. Input each x1,y1,x2,y2... var_x and var_y alternately
or matrix (2*n) type DATA at prompt for DATA.x
2. When you finished to insert DATA, type "end" at prompt for DATA.x
3. If there's no error with DATA sets, function i.linear() and i.polynomial() will be created.
4. Use functions to find unkown value "y"
5. Additionally, data.sub(matrix) and data.subx,data.suby(list) will be made too.
Caution
To stop a program that contains a Request command inside an infinite loop:
• Handheld: Hold down the "on" key and press "enter" repeatedly.
• Windows?: Hold down the "F12" key and press "Enter" repeatedly.
• Macintosh?: Hold down the "F5" key and press "Enter" repeatedly.
1. 기능
기본 데이터를 입력하여 선형 보간법에 따른 조각함수(Piecewise Function) i.linear(x) 와 다항식 보간법(라그랑주)에 따른 함수 i.polynomial(x) 를 생성합니다.
생성된 함수를 이용하여 특정 값(x)에서의, 보간법 예상치(y)를 구합니다.
2. 사용법
2-a. 기본 데이터 입력
- 프로그램의 실행 : inter()
- 기본 DATA 입력
방법 1 : 번갈아 입력 : x1, y1, x2, y2, x3, y3... , (입력이 끝나면 e 또는 end 를 입력)
혹은
방법 2 : 2×N 행렬을 한꺼번에 입력 : x값 입력시에 입력 - DATA 입력시
주의사항
* x 는 크기 순서로 입력할 필요 없음 (자동 sort 됨)
* (x,y) 데이터 쌍이 중복 되어도 괜찮으나, 하나의 x값에 둘 이상의 y값이 존재하면 에러 발생
2-b. 결과 함수의 이용
- 2-a의 입력이 끝나면 결과함수로 사용할 변수명을 물어봄
- 결과함수를 이용하여 추정값을 구함
ex) i.linear(3) 【Enter】 : x=3일 때의 추정값을 구함
2-c. 생성된 함수의 확인 http://www.allcalc.org/5752
- 【MENU】 【1】 【2】 (Action - Recall Definition) 명령으로 사용자 함수에 현재 정의되어 있는 내용을 확인할 수 있습니다.
3. 결과
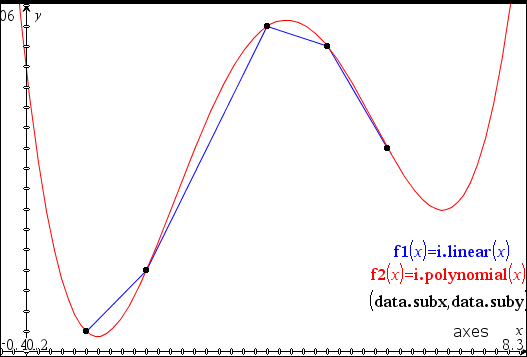
4. 소스코드
Define LibPub inter()=
Prgm
:© Linear and Polynomial Interpolation for TI-nspire
:© Ver 1.2
:© by allcalc (allcalc.org)
:
:© Part A: Input DATA
:
:Local n,data.x,data.y,data
:n:=0
:Loop
: Request "data.x or matrix(2×n) or END",data.x,0
:
:© Exit Loop Condition
: If string(data.x)="end" or string(data.x)="END" or string(data.x)="e" Then
: Exit
: EndIf
:
:© Adding Data
: n+1→n
:© Adding Data with Matrix
: If getType(data.x)="MAT" Then
: n+dim(data.x)[2]-1→n
: If n=dim(data.x)[2] Then
: data.x→data
: Else
: augment(data,data.x)→data
: EndIf
:© Adding Each Data Pair
: Else
: Request "data.y for x="&string(data.x),data.y,0
: If string(data.y)="end" or string(data.y)="END" Then
: Exit
: EndIf
: If n=1 Then
:[[data.x][data.y]]→data
: Else
: augment(data,[[data.x][data.y]])→data
: EndIf
: EndIf
:EndLoop
:
:© Part B : Data Processing
:
:© Part B1 : Data Processing
:Local data.listx,data.listy
:mat▶list(data[1])→data.listx
:mat▶list(data[2])→data.listy
:SortA data.listx,data.listy
:colAugment(list▶mat(data.listx),list▶mat(data.listy))→data
:
:© Part B2 : Section Verification&Consolidation and Slope
:© Verification
:Local i,j,dup
:newList(n)→dup
:For i,1,n-1
: If data[1,i]=data[1,i+1] Then
: 1→dup[i+1]
: If data[2,i]≠data[2,i+1] Then
: Disp "Data Error : ",[["x"]["y"]],"=",subMat(data,1,i,2,i+1)
: Stop
: EndIf
: EndIf
:EndFor
:
:© Consolidation
:© Local data.sub : Make data.sub global var
:subMat(data,1,1,2,1)→data.sub
:For i,2,n
: If dup[i]=0 Then
: augment(data.sub,subMat(data,1,i,2,i))→data.sub
: EndIf
:EndFor
:
:mat▶list(data.sub[1])→data.subx
:mat▶list(data.sub[2])→data.suby
:Disp "data.sub",[["x"]["y"]],"=",data.sub
:
:© Slope for Linear Interpolation
:Local sub.slope,sub.n
:dim(data.sub)[2]→sub.n
:newList(sub.n-1)→sub.slope
:For i,1,sub.n-1
:((data.sub[2,i+1]-data.sub[2,i])/(data.sub[1,i+1]-data.sub[1,i]))→sub.slope[i]
:EndFor
:
:
:© Part C1 : Out Polynomial Function as i.polynomial(x)
:Local poly,f_name
:"i"→f_name
:Request "Input Function name",f_name,0
:If getType(f_name)="NUM" Then
:"i"&string(f_name)→f_name
:Else
: If getType(f_name)≠"STR" Then
: string(f_name)→f_name
: EndIf
:EndIf
:
:"Define "&f_name&".polynomial(var_x)="&string(∑(data.sub[2,i]*∏(when(i≠j,((var_x-data.sub[1,j])/(data.sub[1,i]-data.sub[1,j])),1),j,1,sub.n),i,1,sub.n))→poly
:expr(poly)
:
:© Part C2 : Out Piecewise Linear Interpolation Function as i.linear(x)
:
:Local pf,random.x
:"Define "&f_name&".linear(x)=piecewise("→pf
:For i,1,sub.n-1
: pf&string(sub.slope[i]*(x-data.sub[1,i])+data.sub[2,i])&","&string(data.sub[1,i]≤x≤data.sub[1,i+1])&","→pf
:EndFor
:left(pf,dim(pf)-1)&")"→pf
:expr(pf)
:
:© Part C3 : Display functions usage
:rand()*(data.sub[1,sub.n]-data.sub[1,1])+data.sub[1,1]→random.x
:Disp "Usage : "&f_name&".linear("&string(random.x)&")=",#(f_name&".linear")(random.x)
:Disp f_name&".polynomial("&string(random.x)&")=",#(f_name&".polynomial")(random.x)
:
:Disp "Linear function is =",pf
:Disp "Polynomial function is =",poly
:EndPrgm
-
25
댓글10
-
세상의모든계산기
이 프로그램은 선형 보간법과 라그랑주 보간법을 동시에 구하는 프로그램입니다.
간단하게 선형 보간법의 결과만 필요한 경우에는
별도의 프로그램 파일 혹은 라이브러리를 사용하기보다 statistics(통계) 의 Linear Regression 기능을 이용하는 것이 편합니다.(예제 : http://www.allcalc.org/7826 )
- 1
-
세상의모든계산기
예를 들어
http://www.allcalc.org/2387 의 댓글에 있는 예제를 푼다면
【inter()】
【200】【1250】
【300】【1890】
【e】【Enter】
순으로 DATA 입력을 마치고【i.linear(250)】
으로 목표값을 찾습니다.* 이렇게 DATA 가 2쌍 뿐인 경우에는 i.linear() 함수와 i.polynomial() 함수가 동일한 결과값을 출력합니다.
(단, linear() 함수는 조각함수라서 데이터 범위 안쪽의 값만을 구할 수 있습니다.) - 1
- 2
- 3
- 4
-
3
세상의모든계산기
inter() 함수 결과에 생성된 함수를 출력하는 명령(Disp)을 추가했습니다.
한 줄 표기되어서 알아보기 어렵다고 느끼실 때는
- Menu - Action - Recall Definition
- 아니면 한 줄 표기된 결과를 선택해서 입력창에 붙여넣기 하신 다음 [enter] 하시면 입체적 표현으로 바뀝니다.
세상의모든계산기 님의 최근 댓글
[일반계산기] 매출액 / 원가 / 마진율(=이익율)의 계산. https://allcalc.org/20806 2026 02.08 V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04 1. 분모 먼저 계산 400 × 10000 = 100 × 6000 = GT 결과값 4,600,000 역수 처리 ÷÷== 결과값 0.00000021739 2. 분자 곱하기 ×3 00 00 00 ×4 00 ×1 00 00 최종 결과 = 2,608,695.65217 2026 02.04 해결 방법 1. t=-1 을 기준으로 그래프를 2개로 나누어 표현 ㄴ 근데 이것도 tstep을 맞추지 않으면 문제가 발생할 것기도 하고, 상관이 없을 것 같기도 하고... 모르겠네요. 2. t=-1 이 직접 계산되도록 tstep을 적절하게 조정 tstep=0.1 tstep=0.01 도 해 보고 싶지만, 구간 크기에 따라 최소 tstep 이 변하는지 여기서는 0.01로 설정해도 0.015로 바뀌어버립니다. 그래서 tstep=0.02 로 하는게 최대한 긴 그래프를 얻을 수 있습니다. 2026 02.02