- TI nspire
[TI-nspire] irr, mirr 내부수익률, 수정된 내부수익률 의 계산
-
- 2024.06.14 - 13:45 2015.03.21 - 14:54 3179 7
1. irr() 
irr(CF0,CFList [,CFFreq]) ⇒ value
irr 함수는 투자의 **내부 수익률(IRR)**을 계산하는 재무 함수입니다.
- CF0: 초기 현금 흐름(시간 0)이며 실수여야 합니다.
- CFList: 초기 현금 흐름(CF0) 이후의 현금 흐름 금액 목록입니다.
- CFFreq: (선택 사항) 각 요소가 그룹화된 (연속적인) 현금 흐름 금액의 발생 빈도를 지정하는 목록입니다. 이는 CFList의 해당 요소와 일치합니다. 기본값은 1이며, 값을 입력할 경우 10,000 미만의 양의 정수여야 합니다.
2. mirr() 
mirr(financeRate,reinvestRate,CF0,CFList[,CFFreq])
조정 내부 수익률(Modified Internal Rate of Return, MIRR)을 반환하는 재무 함수입니다.
- financeRate : 현금 흐름 금액에 대해 지불하는 이자율입니다.
- reinvestRate : 현금 흐름을 재투자할 때 적용하는 이자율입니다.
- CF0 : 초기 현금 흐름(시간 0)이며 실수여야 합니다.
- CFList : 초기 현금 흐름(CF0) 이후의 현금 흐름 금액 목록입니다.
- CFFreq : : (선택 사항) 각 요소가 그룹화된 (연속적인) 현금 흐름 금액의 발생 빈도를 지정하는 목록입니다. 이는 CFList의 해당 요소와 일치합니다. 기본값은 1이며, 값을 입력할 경우 10,000 미만의 양의 정수여야 합니다.
IRR과의 차이점:
- IRR은 모든 현금 흐름이 IRR 자체와 동일한 이자율로 재투자된다는 가정을 합니다.
- MIRR은 현금 흐름을 재투자할 때 사용하는 이자율(reinvestRate)을 별도로 고려하여 보다 사실적인 내부 수익률을 계산합니다.
3. 예제
- CF0 = - 200,000 (초기 투자액)
- CF1 = 20,000
- CF2 = 25,000
- CF3 = 30,000
- CF4 = 35,000
- CF5 = 40,000 + (40,000/0.1)
- IRR = ?
- I (InvestRate=financeRate) = 7 %, RI (ReInvestRate) = 4 %, MIRR = ?
※ irr()만 있고, mirr() 기능이 없는 계산기에서의 계산 방법
- 매기 현금흐름 중에서
1.1 【+(플러스) 현금흐름】은 재투자율로 미래가치로 계산,
└ nspire에는 nfv() 함수가 없으므로 npv()
tvmfv() 2단계 거침.
1.2 【-(마이너스) 현금흐름】은 (내부수익률이 아닌!) 시장이자율로 현재가치로 계산
- 【초기투자액】 + 【-(마이너스) 현금흐름】 현가 = 【+현금흐름】 재투자후 미래가치의 현가
를 만족하는 irr 값을 찾으면 그것이 MIRR
-
25
댓글7
-
1
-
1
-
세상의모든계산기
http://kin.naver.com/qna/detail.nhn?d1id=11&dirId=1113&docId=235021440
├ IRR 기능이 없다면, Solve() 기능으로 찾을 수도 있습니다.
└ 단, IRR 은 해가 여러개일 수 있으므로 주의하여야 합니다. -
세상의모든계산기
본문의 예제(irr 구하기)를 시행착오법으로 구하려 한다면, 시도(try)할 값을 npv() 의 I% 에 하나씩 대입해 풀면 됩니다.
정확한 값을 구할 수 있는데, 굳이 이 방법을 쓸 이유는 없겠습니다. 문제에서 요구한 것이 아니라면 말이죠.
-
세상의모든계산기
채권의 만기수익률 & 맥콜레이 듀레이션
http://kin.naver.com/qna/detail.nhn?d1id=11&dirId=1113&docId=239432530
-
세상의모든계산기
재무 계산기(BA II Plus)에서 MIRR 계산 동영상
https://www.youtube.com/watch?v=SGeWLQIMxc4&ab_channel=FIN-Ed
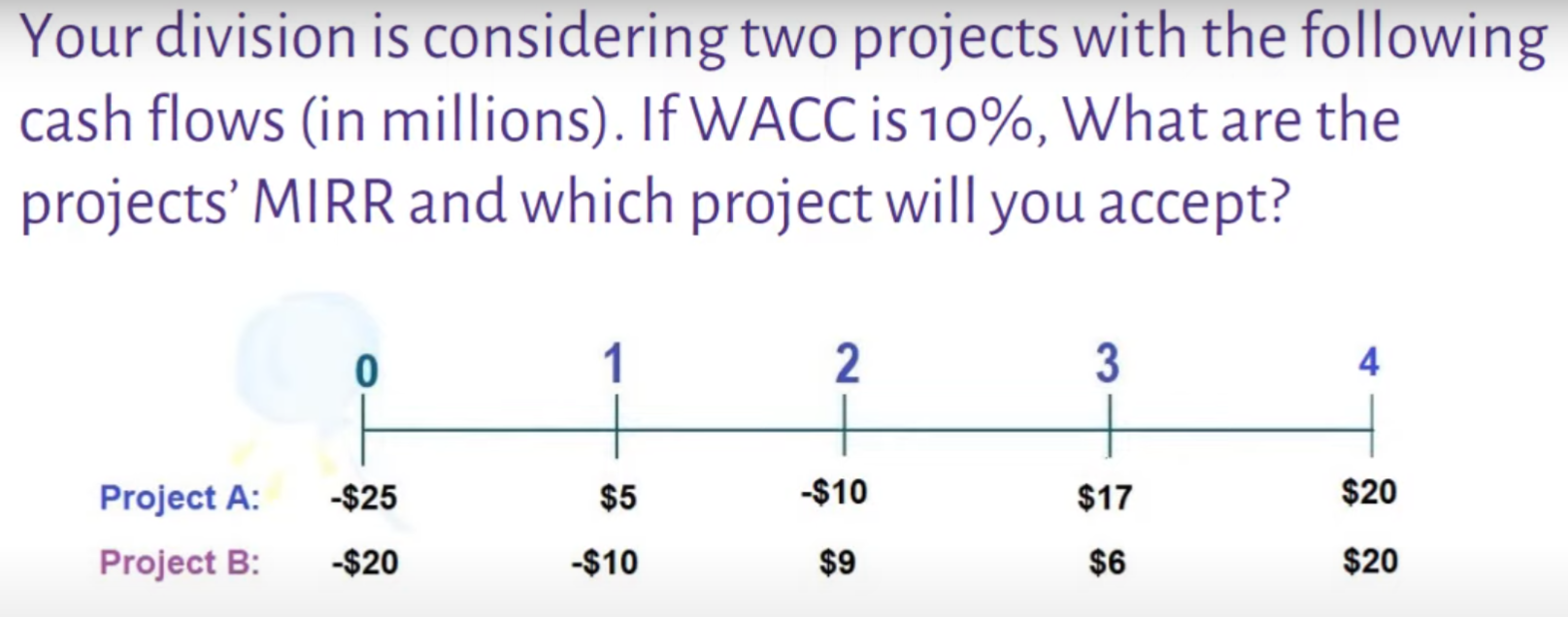
영상 속에서는, WACC=10% 를 사용하여 자본이자율=재투자율=10% 인 것으로 계산하였네요.
ㄴ Project A, B 에 대해 각각 이런 결론이 나온 셈이구요.Project A만 따로 계산해 보면 아래의 과정을 거쳐 나왔습니다.
세상의모든계산기 님의 최근 댓글
뉴턴-랩슨 적분 방정식 시각화 v1.0 body { font-family: 'Pretendard', -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, Helvetica, Arial, sans-serif; display: flex; flex-direction: column; align-items: center; background: #f8f9fa; padding: 40px 20px; margin: 0; color: #333; } .container { background: white; padding: 40px; border-radius: 20px; box-shadow: 0 15px 35px rgba(0,0,0,0.08); max-width: 900px; width: 100%; } header { border-bottom: 2px solid #f1f3f4; margin-bottom: 30px; padding-bottom: 20px; } h1 { color: #1a73e8; margin: 0 0 10px 0; font-size: 1.8em; } p.subtitle { color: #5f6368; margin: 0; font-size: 1.1em; } .equation-box { background: #f1f3f4; padding: 15px; border-radius: 10px; text-align: center; margin-bottom: 30px; font-size: 1.3em; } canvas { border: 1px solid #e0e0e0; border-radius: 12px; background: #fff; width: 100%; height: auto; display: block; } .controls { margin-top: 30px; display: flex; gap: 15px; align-items: center; justify-content: center; flex-wrap: wrap; } button { padding: 12px 25px; border: none; border-radius: 8px; background: #1a73e8; color: white; cursor: pointer; font-weight: 600; font-size: 1em; transition: all 0.2s; box-shadow: 0 2px 5px rgba(26,115,232,0.3); } button:hover { background: #1557b0; transform: translateY(-1px); box-shadow: 0 4px 8px rgba(26,115,232,0.4); } button:active { transform: translateY(0); } button.secondary { background: #5f6368; box-shadow: 0 2px 5px rgba(0,0,0,0.2); } button.secondary:hover { background: #4a4e52; } .status-badge { background: #e8f0fe; color: #1967d2; padding: 8px 15px; border-radius: 20px; font-weight: bold; font-size: 0.9em; } .explanation { margin-top: 40px; padding: 25px; background: #fff8e1; border-left: 5px solid #ffc107; border-radius: 8px; line-height: 1.8; } .explanation h3 { margin-top: 0; color: #856404; } .math-symbol { font-family: 'Times New Roman', serif; font-style: italic; font-weight: bold; color: #d93025; } .code-snippet { background: #202124; color: #e8eaed; padding: 2px 6px; border-radius: 4px; font-family: monospace; } 📊 Newton-Raphson 적분 방정식 시뮬레이터 미분적분학의 기본 정리(FTC)를 이용한 수치해석 시각화 목표 방정식: ∫₀ᴬ (2√x) dx = 20 을 만족하는 A를 찾아라! 계산 시작 (A 추적) 초기화 현재 반복: 0회 💡 시각적 동작 원리 (Newton-Raphson & FTC) Step 1 (오차 측정): 현재 A까지 쌓인 파란색 면적이 목표치(20)와 얼마나 차이나는지 계산합니다. Step 2 (FTC의 마법): 면적의 변화율(미분)은 그 지점의 그래프 높이 f(A)와 같습니다. Step 3 (보정): 다음 A = 현재 A - (면적 오차 / 현재 높이) 공식을 사용하여 A를 이동시킵니다. 결론: 오차를 현재 높이로 나누면, 오차를 메우기 위해 필요한 가로 길이(ΔA)가 나옵니다. 이 과정을 반복하면 정답에 도달합니다! const canvas = document.getElementById('graphCanvas'); const ctx = canvas.getContext('2d'); const iterText = document.getElementById('iterText'); // 수학 설정 const targetArea = 20; const f = (x) => Math.sqrt(x) * 2; // 피적분 함수 f(x) = 2√x const F = (x) => (4/3) * Math.pow(x, 1.5); // 정적분 결과 F(x) = ∫ 2√x dx = 4/3 * x^(3/2) let A = 1.5; // 초기값 let iteration = 0; let animating = false; // 그래프 드로잉 설정 const scale = 50; const offsetX = 60; const offsetY = 380; function drawGrid() { ctx.strokeStyle = '#f1f3f4'; ctx.lineWidth = 1; ctx.beginPath(); for(let i=0; i 2026 04.11 참값 : A = ±2√5 근사값 : A≈±4.472135954999579392818347 2026 04.10 fx-570 ES 입력 결과 초기값 입력 반복 수식 입력 반복 결과 2026 04.10 파이썬 코드 검증 결과 초기값: 5.0 반복 1회차: 4.5000000000 반복 2회차: 4.4722222222 반복 3회차: 4.4721359558 반복 4회차: 4.4721359550 반복 5회차: 4.4721359550 초기값: 10.0 반복 1회차: 6.0000000000 반복 2회차: 4.6666666667 반복 3회차: 4.4761904762 반복 4회차: 4.4721377913 반복 5회차: 4.4721359550 2026 04.10 감사합니다. 주말 잘 보내세요. 2026 03.06