Sharp 계산기의 Advanced D.A.L 이란? (Direct Algebric Logic)
Until the introduction of SHARP's D.A.L., keying in equations had been a complicated process making scientific calculators difficult to use. Introduced in 1992 and an industry-first, SHARP's D.A.L. allows symbols and numbers of an equation to be entered as they are written. Instead of wasting energy on difficult calculator operations, users are free to concentrate on mathematical concepts.
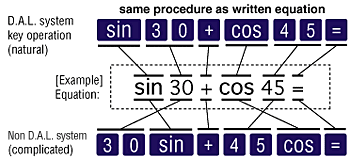
• Non D.A.L. system key operation You have to push the keys in a different order than the actual equation, making the input process confusing. You push the keys in the same order as the actual equation.
출처 : http://www.sharp-world.com/contents/calculator/features/standard/dal/index.html
Keying in an equation is a complicated process with most scientific calculators, which makes them difficult to use. But with D.A.L., a feature unique to Sharp scientific calculators, symbols and numbers in an equation can be keyed in as they are written, allowing users to concentrate on mathematical concepts rather than difficult calculator operations.
출처 : http://sharp-world.com/sc/excite/calculator/text/non-pro/feature1.html
sin(30) 을 입력할 때
D.A.L 아닌 경우에는
순서로 입력해야 했는데,
D.A.L 에서는 글씨 쓸때처럼
순서로 입력 할 수 있다는 이야기...
카시오에서는 이것을 Visually Perfect Algebraic Method (V.P.A.M.) 이라고 부름.
통상은 Infix Notation 이라고 함(wikipedia 인용)
지금은 대부분의 공학용 계산기가 이러한 방식을 사용
* 참조 : http://en.wikipedia.org/wiki/Calculator_input_methods
* 참조 : http://www.allcalc.org/4075 계산기 입력방식의 분류



세상의모든계산기 님의 최근 댓글
[일반계산기] 매출액 / 원가 / 마진율(=이익율)의 계산. https://allcalc.org/20806 2026 02.08 V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04 1. 분모 먼저 계산 400 × 10000 = 100 × 6000 = GT 결과값 4,600,000 역수 처리 ÷÷== 결과값 0.00000021739 2. 분자 곱하기 ×3 00 00 00 ×4 00 ×1 00 00 최종 결과 = 2,608,695.65217 2026 02.04 해결 방법 1. t=-1 을 기준으로 그래프를 2개로 나누어 표현 ㄴ 근데 이것도 tstep을 맞추지 않으면 문제가 발생할 것기도 하고, 상관이 없을 것 같기도 하고... 모르겠네요. 2. t=-1 이 직접 계산되도록 tstep을 적절하게 조정 tstep=0.1 tstep=0.01 도 해 보고 싶지만, 구간 크기에 따라 최소 tstep 이 변하는지 여기서는 0.01로 설정해도 0.015로 바뀌어버립니다. 그래서 tstep=0.02 로 하는게 최대한 긴 그래프를 얻을 수 있습니다. 2026 02.02