- 세상의 모든 계산기 수학, 과학, 공학 이야기 수학 ()
테일러 급수 Taylor Series
테일러 급수(Taylor series)는 함수 \( f(x) \)를 주어진 점 \( a \)를 중심으로 다항식의 형태로 근사하는 방법입니다.
이는 특정 점 주변에서 함수의 값을 근사하기 위해 함수의 도함수 값을 활용하여 무한급수의 형태로 표현합니다.
테일러 급수의 정의
주어진 함수 \( f(x) \)가 \( a \)에서 \( n \)차 미분 가능할 때, \( f(x) \)의 \( a \)를 중심으로 한 테일러 급수는 다음과 같이 정의됩니다:
\[
f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \frac{f'''(a)}{3!}(x - a)^3 + \cdots
\]
즉, 일반적인 형태는 다음과 같습니다:
\[
f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x - a)^n
\]
여기서:
- \( f^{(n)}(a) \)는 \( f(x) \)의 \( n \)차 미분을 \( a \)에서 평가한 값입니다.
- \( n! \)는 \( n \)의 팩토리얼로, \( n! = n \times (n-1) \times \cdots \times 2 \times 1 \)입니다.
- \( (x - a)^n \)는 \( x \)와 \( a \)의 차이를 \( n \)차까지 곱한 것입니다.
테일러 급수의 적용
테일러 급수는 다음과 같은 경우에 유용합니다:
1. 근사 계산: 복잡한 함수를 다항식으로 근사하여 계산을 간단히 할 수 있습니다.
2. 해석적 함수 연구: 함수의 성질을 분석하고 극한, 연속성, 미분 가능성을 연구하는 데 도움을 줍니다.
3. 수치해석: 수치적 방법에서 많은 알고리즘의 근본이 됩니다.
예시
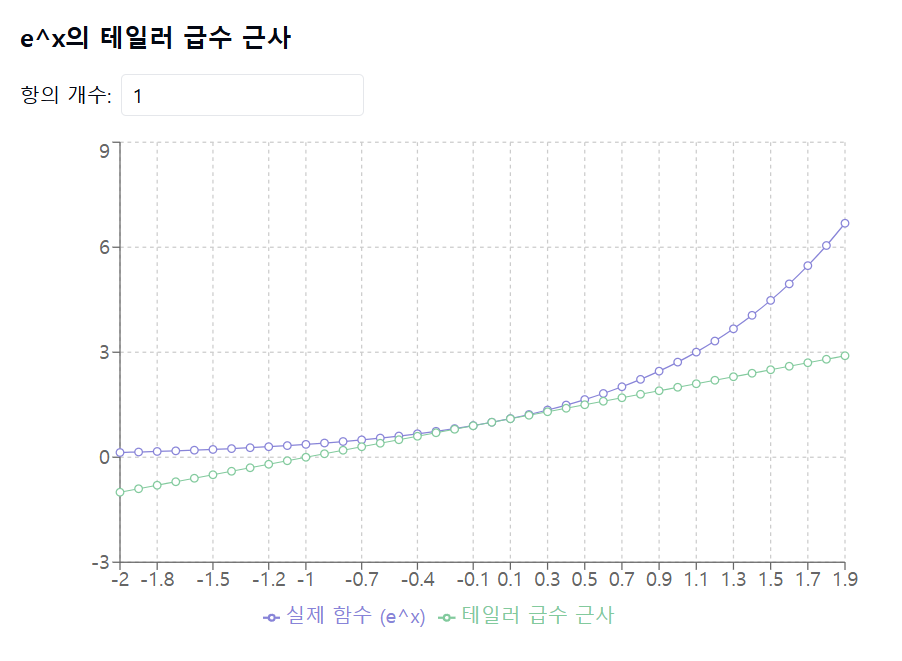
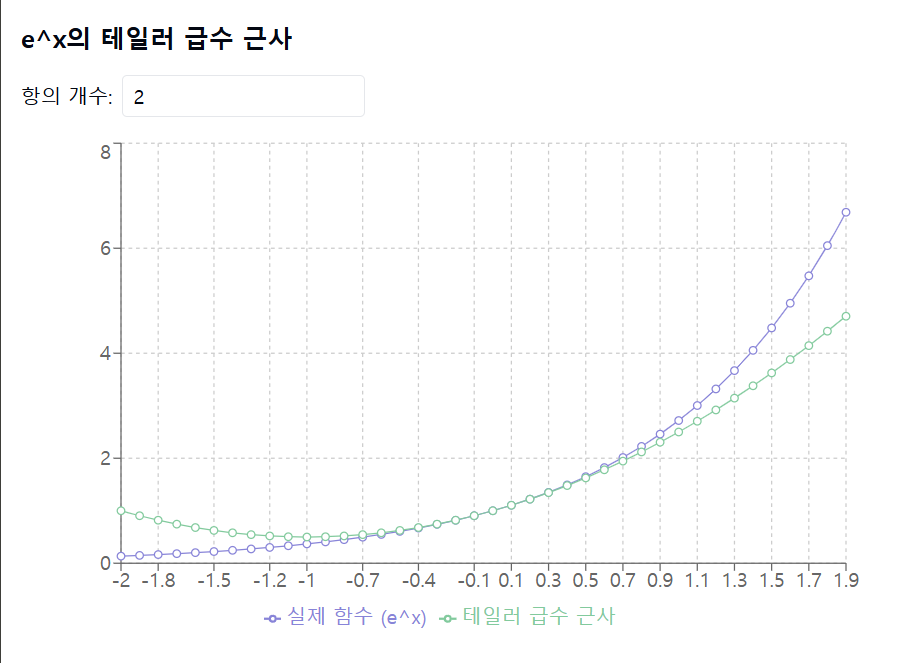
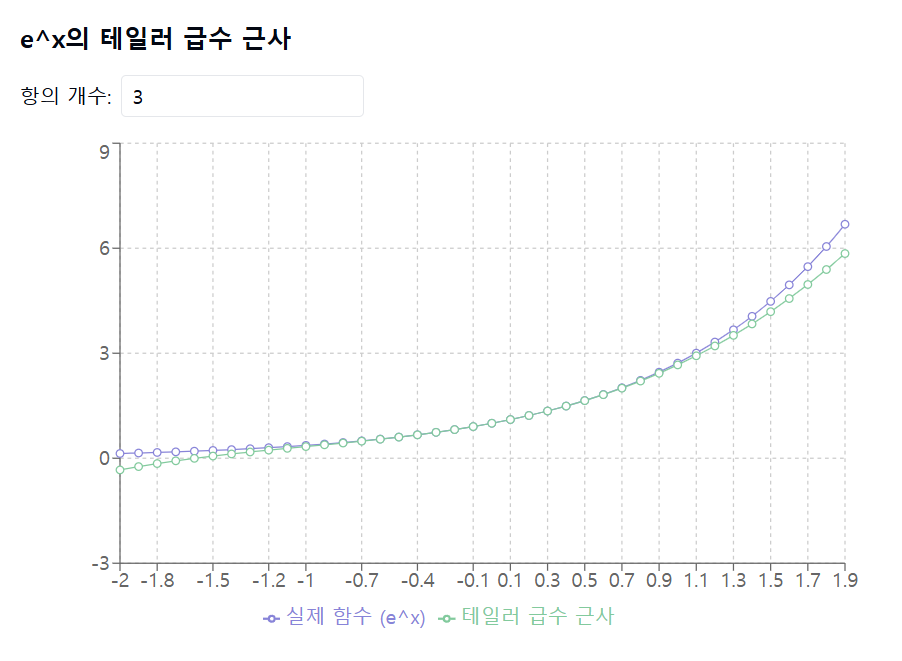
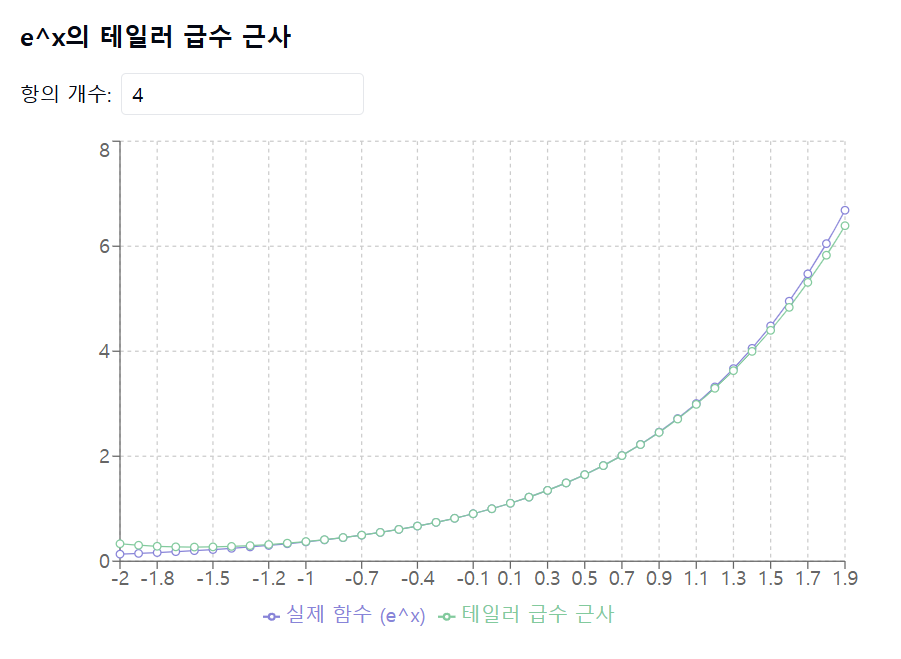
함수 \( e^x \)의 테일러 급수는 \( a = 0 \)을 중심으로 하면 다음과 같이 됩니다:
\[
e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}
\]
또한, \( \sin(x) \)의 테일러 급수는 다음과 같습니다:
\[
\sin(x) = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n + 1)!}x^{2n + 1}
\]
이러한 테일러 급수는 \( x \)가 0에 가까운 경우 \( e^x \)와 \( \sin(x) \)의 값에 매우 잘 근사합니다.
결론
테일러 급수는 함수 근사의 강력한 도구로, 미적분학, 물리학, 공학 등 다양한 분야에서 널리 사용됩니다. 이를 통해 복잡한 함수도 간단한 다항식으로 접근하여 다양한 문제를 해결할 수 있습니다.
참고

http://navercast.naver.com/contents.nhn?rid=22&contents_id=5561
https://ko.wikipedia.org/wiki/%ED%85%8C%EC%9D%BC%EB%9F%AC_%EA%B8%89%EC%88%98
댓글6
-
세상의모든계산기
[TI-nspire] 의 taylor() 내장 함수
taylor(sin(x),x,13)

ㄴ 상단 : Degree, 하단 : Radian
* 이런 저런 이유로 각도 설정은 항상 Radian 으로 하는 것이 좋음.
-
-
세상의모든계산기
예시에서 0 을 중심으로 테일러 급수를 전개한 이유는?
테일러 급수를 0을 중심으로 전개하면 '매클로린 급수'라고도 불리는 특별한 경우의 테일러 급수가 됩니다.
- 계산의 단순화: 0을 중심으로 전개하면 계산이 상대적으로 간단해집니다. x^n 항의 계수가 f^(n)(0) / n!로 표현되어, 많은 함수에서 이 값을 쉽게 계산할 수 있습니다.
- 대칭성: 많은 중요한 함수들(예: e^x, sin(x), cos(x))이 원점에 대해 대칭적인 성질을 가집니다. 0을 중심으로 전개하면 이러한 대칭성을 잘 활용할 수 있습니다.
- 표준화: 0을 기준점으로 사용하면 다양한 함수들을 일관된 방식으로 비교하고 분석할 수 있습니다.
- 수학적 편의성: 많은 수학적 정리와 응용에서 0을 중심으로 한 급수 전개가 유용하게 사용됩니다.
- 오차 분석: 0 주변에서의 근사는 오차 분석이 상대적으로 쉽습니다.
-
세상의모든계산기
테일러 급수의 오차 한계는?
테일러 급수에서 오차는 보통 테일러 급수의 n차 항까지 근사했을 때 실제 함수 값과의 차이로 정의됩니다.
이 오차를 나타내는 대표적인 표현이 테일러 정리의 나머지항(Remainder Term)입니다.
일반적으로 오차의 한계를 제시할 때는 라그랑주 잔여항(Lagrange Remainder) 또는 코시 잔여항(Cauchy Remainder)를 사용합니다.
만약 어떤 함수 \( f(x) \)를 \( a \)를 중심으로 한 테일러 급수로 근사한다고 할 때, 테일러 급수의 \( n \)차 항까지 근사한 오차는 다음과 같은 형태로 주어집니다.
라그랑주 잔여항에 의한 오차
라그랑주 잔여항 \( R_n(x) \)은 다음과 같이 표현됩니다:
\[
R_n(x) = \frac{f^{(n+1)}(c)}{(n+1)!} (x - a)^{n+1}
\]여기서:
- \( f^{(n+1)}(c) \)는 \( a \)와 \( x \) 사이의 어떤 점 \( c \)에서의 \( (n+1) \)차 미분값입니다.
- \( (n+1)! \)은 \( n+1 \) 팩토리얼입니다.
- \( (x - a)^{n+1} \)는 \( x \)와 중심 \( a \) 간의 거리의 \( (n+1) \)제곱입니다.- 테일러 전개를 통해 n번째 항까지 사용하였다면, n+1번째 항이 오차 한계에 해당함을 알 수 있습니다.
이 표현을 통해 오차의 크기를 다음과 같이 한정할 수 있습니다:
\[
|R_n(x)| \leq \frac{\max_{c \in [a, x]} |f^{(n+1)}(c)|}{(n+1)!} |x - a|^{n+1}
\]
따라서, 주어진 구간에서 \( f^{(n+1)}(c) \)의 최대값을 알면, 이 잔여항을 이용하여 테일러 급수 근사 오차의 한계를 추정할 수 있습니다.이 오차는 테일러 급수의 차수가 높아질수록 작아지며, 중심에 가까운 점일수록 더 정확한 근사를 제공합니다.
-
1
세상의모든계산기
예) 구간[3,5] 에서 f(x)=√x 의 근사값을 a=4 에서의 2차 테일러 다항식을 이용하여 구할 때, 테일러 부등식에 의한 오차의 한계로 가장 적절한 것은?
(단, $ \dfrac{1}{3^{5/2}} \approx 0.064, \dfrac{1}{4^{5/2}} \approx 0.031, \dfrac{1}{5^{5/2}} \approx 0.018) $)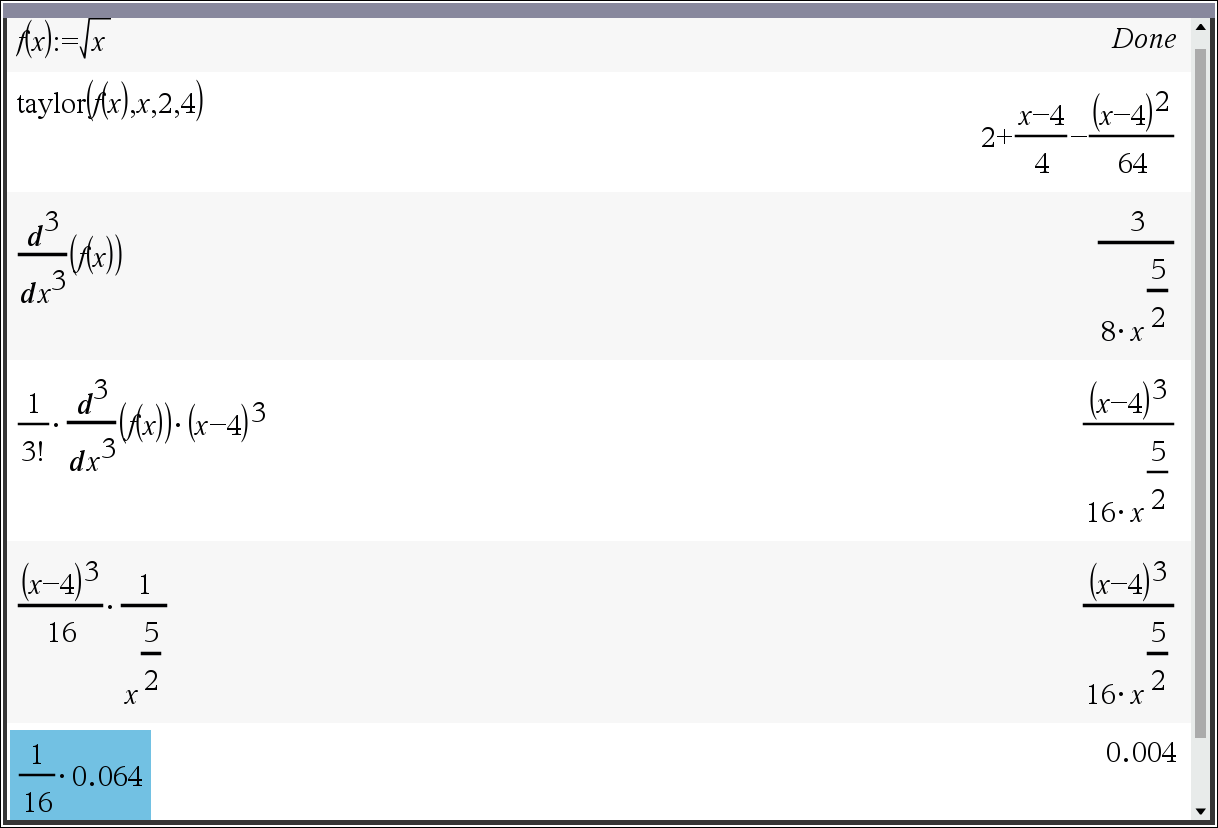


세상의모든계산기 님의 최근 댓글
쌀집계산기로 연립방정식 계산하기 - 크래머/크레이머/크라메르 공식 적용 https://allcalc.org/56739 3. 'x' 값 구하기 계산기 조작법 목표: x = Dx / D = [(c×e) - (b×f)] / [(a×e) - (b×d)] 계산하기 1단계: 분모 D 계산 (메모리 활용) 1 * 1 M+ : 메모리(M)에 1를 더합니다. (현재 M = 1) -0.1 * -0.2 M- : 메모리(M)에서 0.02를 뺍니다. (현재 M = 0.98 = 0.98) 이로써 메모리(MR)에는 분모 0.98가 저장됩니다. 2단계: 분자 Dx 계산 후 나누기 78000 * 1 : 78000를 계산합니다. = : GT에 더합니다. -0.1 * 200000 : -20000를 계산합니다. ± = : 부호를 뒤집어 GT에 넣습니다. // sign changer 버튼 사용 GT : GT를 불러옵니다. GT는 98000 (분자 Dx) 값입니다. ÷ MR = : 위 결과(98000)를 메모리(MR)에 저장된 분모 D(0.98)로 나누어 최종 x값 100,000를 구합니다. 4. 'y' 값 구하기 계산기 조작법 목표: y = Dy / D = [(a×f) - (c×d)] / [(a×e) - (b×d)] 계산하기 1단계: 분모 D 계산 (메모리 활용) 'x'에서와 분모는 동일하고 메모리(MR)에 0.98가 저장되어 있으므로 패스합니다. 2단계: 분자 Dy 계산 후 나누기 GT ± = : GT를 불러오고 부호를 뒤집어 GT에 더합니다. GT가 0으로 리셋됩니다. 【AC】를 누르면 M은 유지되고 GT만 리셋되는 계산기도 있으니 확인해 보세요. 1 * 200000 : 200000를 계산합니다. = : GT에 더합니다. 78000 * -0.2 : -15600를 계산합니다. ± = : 부호를 뒤집어 GT에 넣습니다. GT : GT를 불러옵니다. 215600 (분자 Dy) 값입니다. ÷ MR = : 위 결과(215600)를 메모리(MR)에 저장된 분모 D(0.98)로 나누어 최종 y값 220,000를 구합니다. x, y 값을 이용해 최종 결과를 구합니다. 2026 01.18 크레이머 = 크레머 = 크라메르 공식 = Cramer's Rule https://allcalc.org/8985 2026 01.18 부호 변경 버튼 https://allcalc.org/52092 2026 01.18 [fx-570 CW] 와의 차이 CW에 【×10x】버튼이 사라진 것은 아닌데, 버튼을 누를 때 [ES][EX] 처럼 특수기호 뭉치가 생성되는 것이 아니고, 【×】【1】【0】【xㅁ】 버튼이 차례로 눌린 효과가 발생됨. ※ 계산 우선순위 차이가 발생할 수 있으므로 주의. 괄호로 해결할 것! 2026 01.18 26년 1월 기준 국가 전문자격 종류 가맹거래사 감정사 감정평가사 검량사 검수사 경매사 경비지도사 경영지도사 공인노무사 공인중개사 관광통역안내사 관세사 국가유산수리기능자(24종목) 국가유산수리기술자 국내여행안내사 기술지도사 농산물품질관리사 물류관리사 박물관 및 미술관 준학예사 변리사 사회복지사 1급 산업보건지도사 산업안전지도사 세무사 소방시설관리사 소방안전교육사 손해평가사 수산물품질관리사 정수시설운영관리사 주택관리사보 청소년상담사 청소년지도사 한국어교육능력검정시험 행정사 호텔경영사 호텔관리사 호텔서비스사 2026 01.17