- 세상의 모든 계산기 수학, 과학, 공학 이야기 수학 ()
테일러 급수 Taylor Series
-
- 2024.11.01 - 23:36 2015.10.12 - 20:57 3487 6
테일러 급수(Taylor series)는 함수 \( f(x) \)를 주어진 점 \( a \)를 중심으로 다항식의 형태로 근사하는 방법입니다.
이는 특정 점 주변에서 함수의 값을 근사하기 위해 함수의 도함수 값을 활용하여 무한급수의 형태로 표현합니다.
테일러 급수의 정의
주어진 함수 \( f(x) \)가 \( a \)에서 \( n \)차 미분 가능할 때, \( f(x) \)의 \( a \)를 중심으로 한 테일러 급수는 다음과 같이 정의됩니다:
\[
f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \frac{f'''(a)}{3!}(x - a)^3 + \cdots
\]
즉, 일반적인 형태는 다음과 같습니다:
\[
f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x - a)^n
\]
여기서:
- \( f^{(n)}(a) \)는 \( f(x) \)의 \( n \)차 미분을 \( a \)에서 평가한 값입니다.
- \( n! \)는 \( n \)의 팩토리얼로, \( n! = n \times (n-1) \times \cdots \times 2 \times 1 \)입니다.
- \( (x - a)^n \)는 \( x \)와 \( a \)의 차이를 \( n \)차까지 곱한 것입니다.
테일러 급수의 적용
테일러 급수는 다음과 같은 경우에 유용합니다:
1. 근사 계산: 복잡한 함수를 다항식으로 근사하여 계산을 간단히 할 수 있습니다.
2. 해석적 함수 연구: 함수의 성질을 분석하고 극한, 연속성, 미분 가능성을 연구하는 데 도움을 줍니다.
3. 수치해석: 수치적 방법에서 많은 알고리즘의 근본이 됩니다.
예시
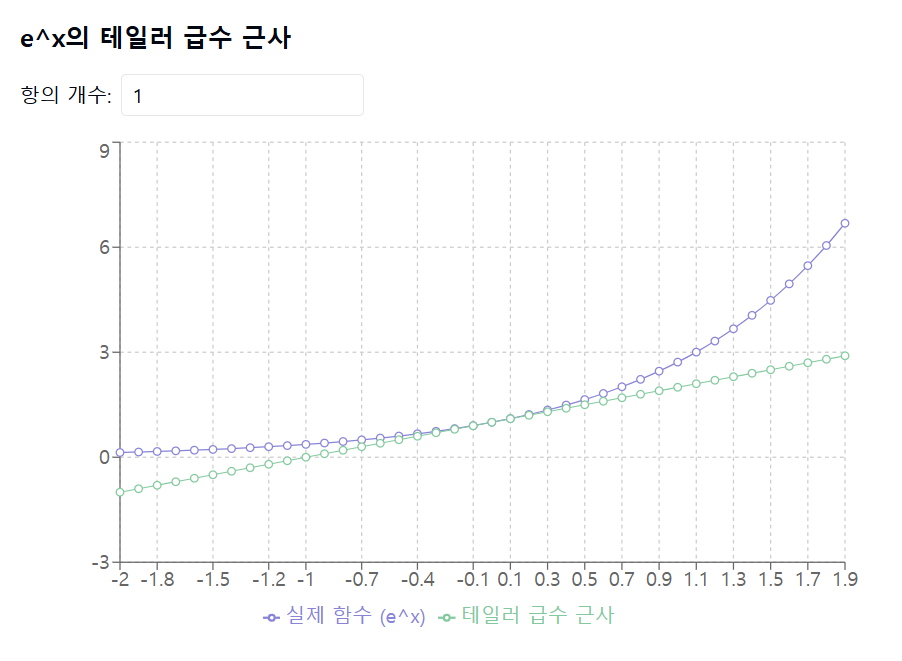
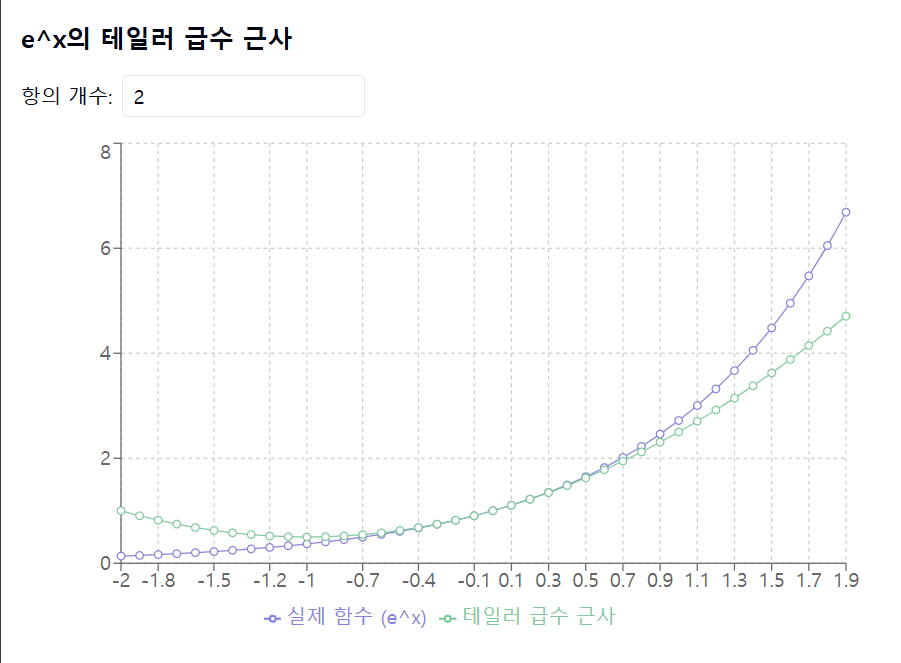
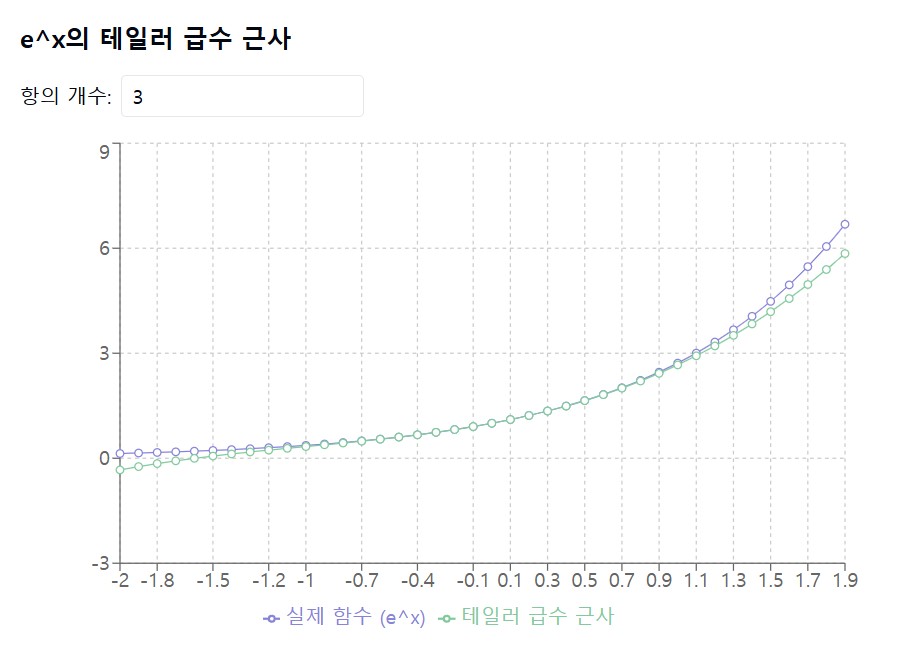
함수 \( e^x \)의 테일러 급수는 \( a = 0 \)을 중심으로 하면 다음과 같이 됩니다:
\[
e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}
\]
또한, \( \sin(x) \)의 테일러 급수는 다음과 같습니다:
\[
\sin(x) = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n + 1)!}x^{2n + 1}
\]
이러한 테일러 급수는 \( x \)가 0에 가까운 경우 \( e^x \)와 \( \sin(x) \)의 값에 매우 잘 근사합니다.
결론
테일러 급수는 함수 근사의 강력한 도구로, 미적분학, 물리학, 공학 등 다양한 분야에서 널리 사용됩니다. 이를 통해 복잡한 함수도 간단한 다항식으로 접근하여 다양한 문제를 해결할 수 있습니다.
참고
http://navercast.naver.com/contents.nhn?rid=22&contents_id=5561
https://ko.wikipedia.org/wiki/%ED%85%8C%EC%9D%BC%EB%9F%AC_%EA%B8%89%EC%88%98
-
25
댓글6
-
세상의모든계산기
[TI-nspire] 의 taylor() 내장 함수
taylor(sin(x),x,13)
ㄴ 상단 : Degree, 하단 : Radian
* 이런 저런 이유로 각도 설정은 항상 Radian 으로 하는 것이 좋음.
-
-
세상의모든계산기
예시에서 0 을 중심으로 테일러 급수를 전개한 이유는?
테일러 급수를 0을 중심으로 전개하면 '매클로린 급수'라고도 불리는 특별한 경우의 테일러 급수가 됩니다.
- 계산의 단순화: 0을 중심으로 전개하면 계산이 상대적으로 간단해집니다. x^n 항의 계수가 f^(n)(0) / n!로 표현되어, 많은 함수에서 이 값을 쉽게 계산할 수 있습니다.
- 대칭성: 많은 중요한 함수들(예: e^x, sin(x), cos(x))이 원점에 대해 대칭적인 성질을 가집니다. 0을 중심으로 전개하면 이러한 대칭성을 잘 활용할 수 있습니다.
- 표준화: 0을 기준점으로 사용하면 다양한 함수들을 일관된 방식으로 비교하고 분석할 수 있습니다.
- 수학적 편의성: 많은 수학적 정리와 응용에서 0을 중심으로 한 급수 전개가 유용하게 사용됩니다.
- 오차 분석: 0 주변에서의 근사는 오차 분석이 상대적으로 쉽습니다.
-
세상의모든계산기
테일러 급수의 오차 한계는?
테일러 급수에서 오차는 보통 테일러 급수의 n차 항까지 근사했을 때 실제 함수 값과의 차이로 정의됩니다.
이 오차를 나타내는 대표적인 표현이 테일러 정리의 나머지항(Remainder Term)입니다.
일반적으로 오차의 한계를 제시할 때는 라그랑주 잔여항(Lagrange Remainder) 또는 코시 잔여항(Cauchy Remainder)를 사용합니다.
만약 어떤 함수 \( f(x) \)를 \( a \)를 중심으로 한 테일러 급수로 근사한다고 할 때, 테일러 급수의 \( n \)차 항까지 근사한 오차는 다음과 같은 형태로 주어집니다.
라그랑주 잔여항에 의한 오차
라그랑주 잔여항 \( R_n(x) \)은 다음과 같이 표현됩니다:
\[
R_n(x) = \frac{f^{(n+1)}(c)}{(n+1)!} (x - a)^{n+1}
\]여기서:
- \( f^{(n+1)}(c) \)는 \( a \)와 \( x \) 사이의 어떤 점 \( c \)에서의 \( (n+1) \)차 미분값입니다.
- \( (n+1)! \)은 \( n+1 \) 팩토리얼입니다.
- \( (x - a)^{n+1} \)는 \( x \)와 중심 \( a \) 간의 거리의 \( (n+1) \)제곱입니다.- 테일러 전개를 통해 n번째 항까지 사용하였다면, n+1번째 항이 오차 한계에 해당함을 알 수 있습니다.
이 표현을 통해 오차의 크기를 다음과 같이 한정할 수 있습니다:
\[
|R_n(x)| \leq \frac{\max_{c \in [a, x]} |f^{(n+1)}(c)|}{(n+1)!} |x - a|^{n+1}
\]
따라서, 주어진 구간에서 \( f^{(n+1)}(c) \)의 최대값을 알면, 이 잔여항을 이용하여 테일러 급수 근사 오차의 한계를 추정할 수 있습니다.이 오차는 테일러 급수의 차수가 높아질수록 작아지며, 중심에 가까운 점일수록 더 정확한 근사를 제공합니다.
-
1
세상의모든계산기
예) 구간[3,5] 에서 f(x)=√x 의 근사값을 a=4 에서의 2차 테일러 다항식을 이용하여 구할 때, 테일러 부등식에 의한 오차의 한계로 가장 적절한 것은?
(단, $ \dfrac{1}{3^{5/2}} \approx 0.064, \dfrac{1}{4^{5/2}} \approx 0.031, \dfrac{1}{5^{5/2}} \approx 0.018) $)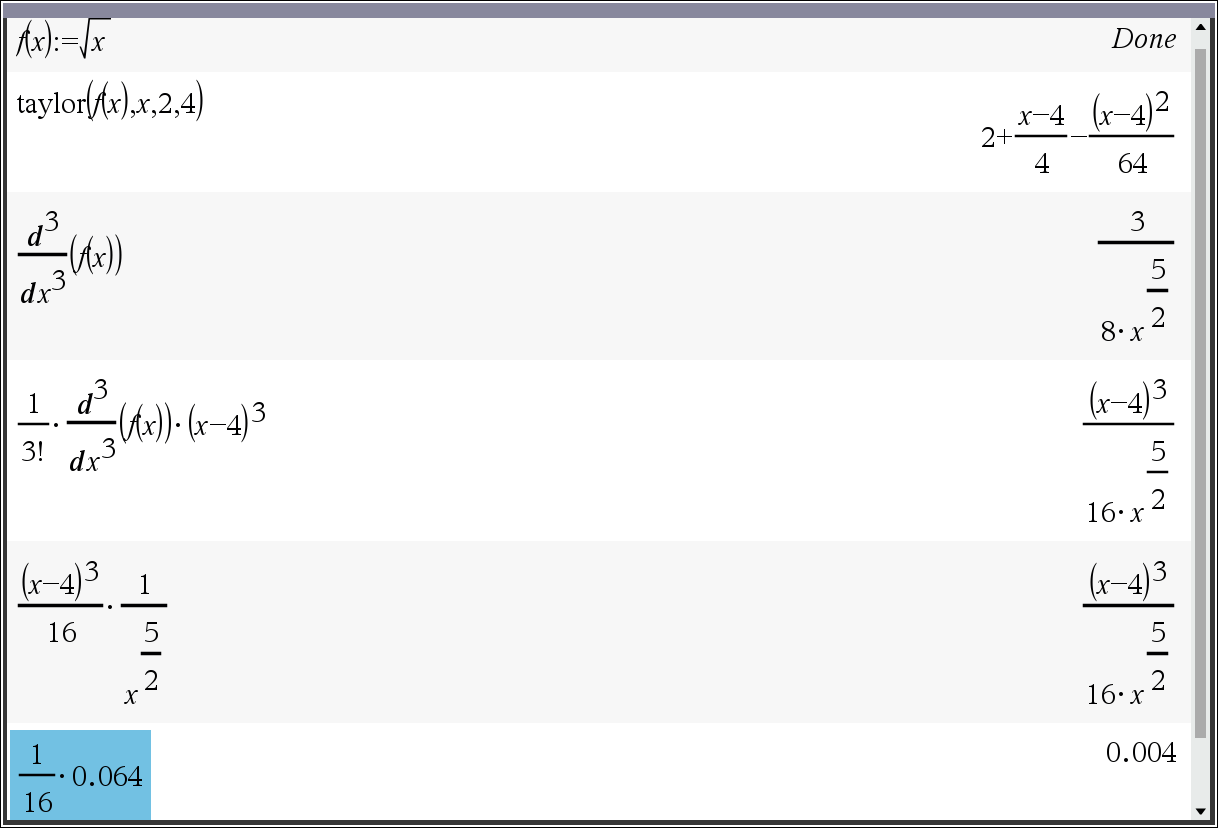
세상의모든계산기 님의 최근 댓글
엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10 엑셀 / 행의 최대 개수, 열의 최대 개수, 셀의 최대 개수 엑셀의 행 개수 제한은 파일 형식에 따라 다르며, 최신 .xlsx 파일 형식은 시트당 최대 1,048,576행까지 지원하지만, 구형 .xls 파일은 65,536행으로 제한됩니다. 따라서 대용량 데이터를 다룰 때는 반드시 최신 파일 형식(.)으로 저장해야 하며, 행과 열의 총 수는 1,048,576행 x 16,384열이 최대입니다. 주요 행 개수 제한 사항: 최신 파일 형식 (.xlsx, .xlsm, .xlsb 등): 시트당 1,048,576행 (2^20). 구형 파일 형식 (.xls): 시트당 65,536행 (2^16). 그 외 알아두면 좋은 점: 최대 행 수: 1,048,576행 (100만여개) 최대 열 수: 16,384열 (XFD) 대용량 데이터 처리: 65,536행을 초과하는 데이터를 다루려면 반드시 .xlsx 형식으로 저장하고 사용해야 합니다. 문제 해결: 데이터가 많아 엑셀이 멈추거나 오류가 발생하면, 불필요한 빈 행을 정리하거나 Inquire 추가 기능을 활용하여 파일을 최적화할 수 있습니다. 2026 02.10 [일반계산기] 매출액 / 원가 / 마진율(=이익율)의 계산. https://allcalc.org/20806 2026 02.08 V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04