- CASIO 9860
[fx-9860G] 각도(Angle)의 설정, 단위 입력 및 변환
-
- 2024.10.08 - 22:22 2015.03.27 - 15:36 12658 1
1. 각도의 사전 설정
【SHIFT】【MENU】 에서 방향 키로 Angle 항목을 찾아간 후 원하는 단위 선택
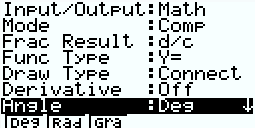
- 【F1】 Deg(도)
- 【F2】 Rad(호도, 라디안)
- 【F3】 Gra(그라디안)
2. 각도단위의 직접 입력 (사전 설정 단위을 무시함)
예시
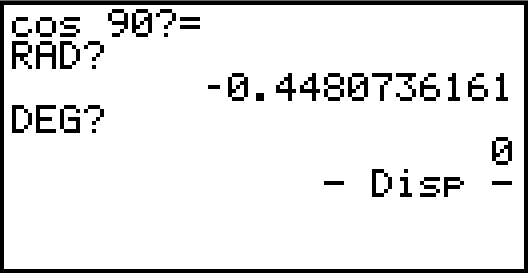
설정은 radian 이더라도, 강제로 degree 단위로 입력
- 방법1
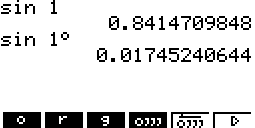
【OPTN】【F6】【F5】 (Angle)
화면하단에 나온 각도단위 표시를 입력(【F1】~【F3】)
- 방법2
CATALOG 에서 직접 찾아서 입력
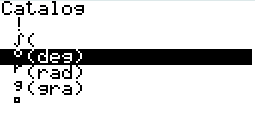
주의! (DMS 단위)
Degree 기호와 달리 DMS 단위기호(□)로는 강제 단위 인식이 불가능.
(DMS단위)˚ 와 같이 추가로 Degree 단위를 추가로 붙여야만 강제 인식이 가능.
3. 팁 (키가 고장났다구요?)
【F1】 ~ 【F6】 키가 고장나서 설정을 변경할 수 없는 경우라면?
http://kin.naver.com/qna/detail.nhn?d1id=11&dirId=1113&docId=234526997
π÷180 D 로 변수에 저장한 다음에, sin (60D) 와 같이 입력.
* 고장이 아니더라도 위와 같이 D나 G에 단위변환값을 넣어놓고 사용하면, D/G 두가지 각도단위를 동시에 사용하기 쉬움
4. 결과값의 변환 to DMS (도분초)
【F4】 로 화살표가 위에 있는 [$\overleftarrow{˚´˝} $] 를 선택
-
25
댓글1
-
세상의모든계산기
Program Mode
방법 1) 일반 모드에서 변경하고 프로그램 모드로 돌아오면 변경한 설정이 적용됩니다.
프로그램 모드 내(프로그램 LIST 화면)에서는 【SHIFT】【MENU】SET UP 을 눌러도 RUN.MAT 모드와 같은 각도 설정 화면이 뜨지 않기 때문에,
일반 모드에서 변경하고 프로그램 모드로 돌아오는 것입니다.
방법 2) 프로그램 외부의 각도 설정에 따라 프로그램 실행 결과가 달라지는 것은 바람직하지 않기 때문에
프로그램 내부에서 각도 설정을 명시적으로 입력하는 것이 좋습니다.
입력 방법 :
프로그램 작성 중 【SHIFT】【MENU】SET UP 을 누르면 화면 하단에 【F1】ANGL 탭이 나옵니다.
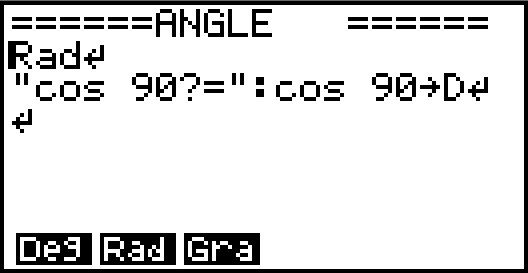
【F1】~【F3】 으로 원하는 각도 단위를 선택하면,
프로그램 내에 각도 설정 명령이 입력됩니다.
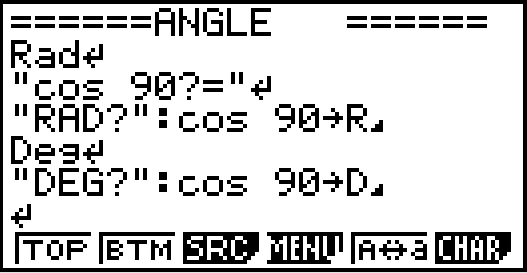
세상의모든계산기 님의 최근 댓글
엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10 엑셀 / 행의 최대 개수, 열의 최대 개수, 셀의 최대 개수 엑셀의 행 개수 제한은 파일 형식에 따라 다르며, 최신 .xlsx 파일 형식은 시트당 최대 1,048,576행까지 지원하지만, 구형 .xls 파일은 65,536행으로 제한됩니다. 따라서 대용량 데이터를 다룰 때는 반드시 최신 파일 형식(.)으로 저장해야 하며, 행과 열의 총 수는 1,048,576행 x 16,384열이 최대입니다. 주요 행 개수 제한 사항: 최신 파일 형식 (.xlsx, .xlsm, .xlsb 등): 시트당 1,048,576행 (2^20). 구형 파일 형식 (.xls): 시트당 65,536행 (2^16). 그 외 알아두면 좋은 점: 최대 행 수: 1,048,576행 (100만여개) 최대 열 수: 16,384열 (XFD) 대용량 데이터 처리: 65,536행을 초과하는 데이터를 다루려면 반드시 .xlsx 형식으로 저장하고 사용해야 합니다. 문제 해결: 데이터가 많아 엑셀이 멈추거나 오류가 발생하면, 불필요한 빈 행을 정리하거나 Inquire 추가 기능을 활용하여 파일을 최적화할 수 있습니다. 2026 02.10 [일반계산기] 매출액 / 원가 / 마진율(=이익율)의 계산. https://allcalc.org/20806 2026 02.08 V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04