- TI nspire
[TI-nspire] 통계 - normCdf 누적분포함수, 정규분포 문제 풀이, feat. binomcdf
-
- 2025.06.04 - 06:18 2015.10.13 - 15:56 3093 3
1. 정규분포
normCdf(lowBound,upBound[,μ[,σ]]) ⇒
number if lowBound and upBound are numbers, list if lowBound and upBound are lists
Computes the normal distribution probability between lowBound and upBound for the specified μ (default=0) and σ (default=1).
For P(X ≤ upBound), set lowBound = -9E999.
문제 출처 : http://math7.tistory.com/49
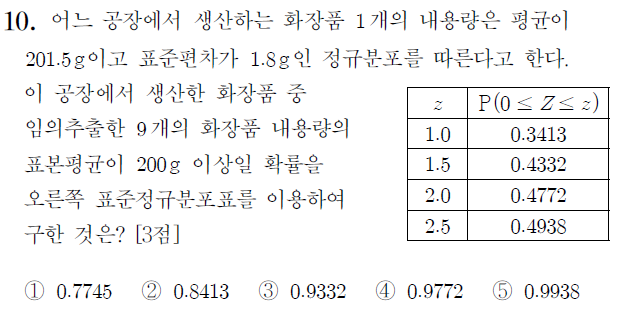
1. 평균 800, 표준편차 40 정규분포 
x≤750 일 확률?
normCdf(−∞,750,800,40)
= normCdf(−∞,−1.25,0,1) = normCdf(−∞,−1.25)
= 0.10564983896266
2. 평균 11, 분산 16 정규분포 20 ≤ x 일 확률?
normCdf(20,∞,11,√(16))
= normCdf(2.25,∞,0,1) = normCdf(2.25,∞)
= 0.012224433401682
3. 평균 70, 표준편차 8 정규분포 80 ≤ x ≤ 90 학생의 비율?
normCdf(80,90,70,8)
= normCdf(1.25,2.5,0,1) = normCdf(1.25,2.5)
= 0.099440159109161
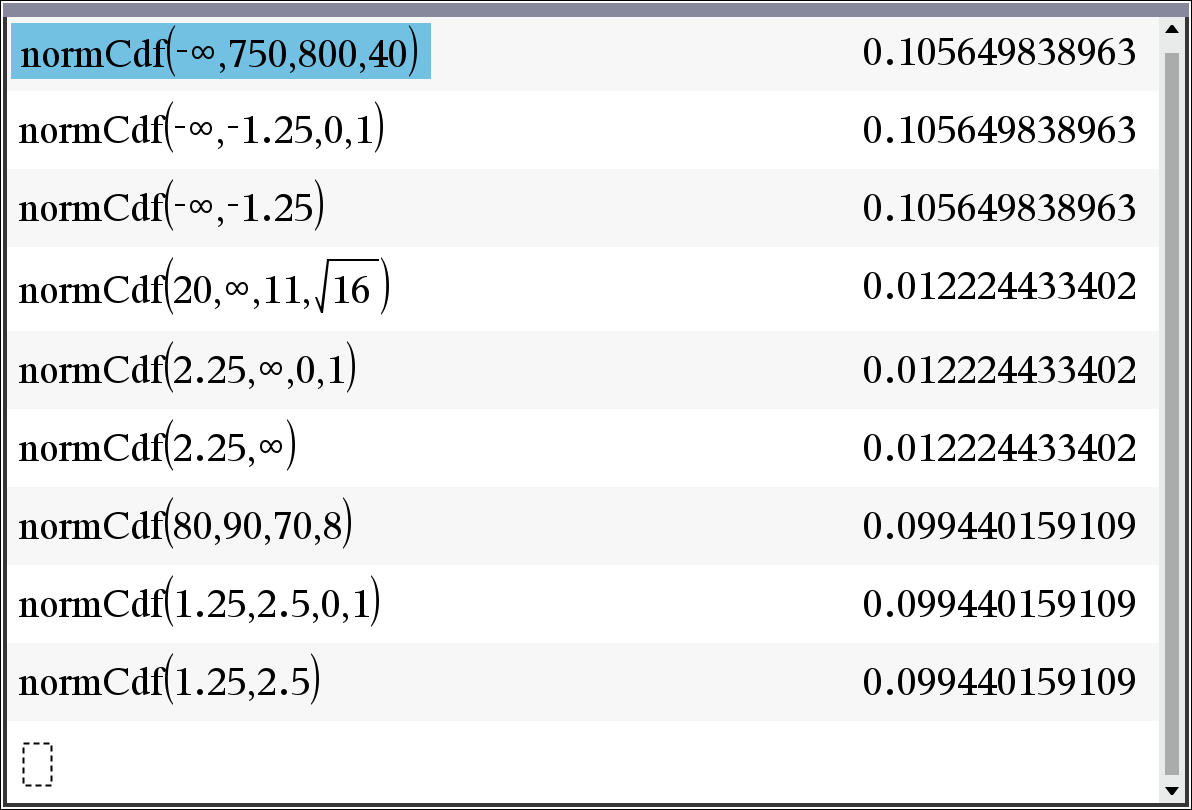
※ 표준화 하지 않아도, 계산기로 즉시 결과를 구할 수 있다.
표준화하는 이유는 표준화되지 않은 확률밀도함수를 매번 적분하기가 까다로워서인데, 계산기는 매번 적분하는데 큰 무리가 없기 때문에 굳이 표준화하는 수고를 거칠 필요가 없음. (맞나?)
2. 이항분포 vs 정규분포
문제 출처 : http://suhak.tistory.com/110
1. 검은 공 1 + 흰 공 3 인 주머니에서 공을 꺼내보고 다시 넣는다. 192회 시행시 검은 공이 48번 이상 60번 이하 나올 확률은?
└ 
정규분포와 이항분포는 가까울 뿐, 똑같지는 않다!
2. 주사위 450회 던질 때 3의 배수가 나온 횟수가 130회 이상 170회 이하일 확률?
3. 주의
normCDF() 계산 결과값에 오차가 조금 있는 듯 합니다.
-
25
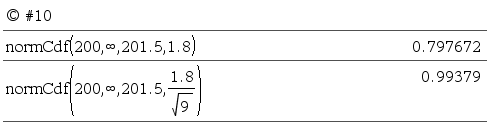
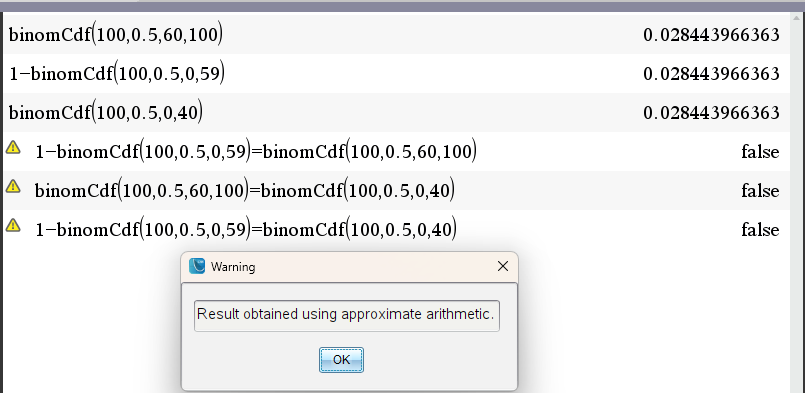
세상의모든계산기 님의 최근 댓글
그래프로 확인 매우 작은 구간으로 그래프를 확대해 보면 불연속적인 모습이 확인됩니다. 이것은 한계 digits(15자리) 이상을 처리하지 못하기 때문입니다. 2025 10.21 tns 파일 첨부 sol_num_vs_exact.tns 2025 10.21 검증하면 1번 식을 x에 대해 정리하고, → 그 x 값을 2번 식에 대입해 넣으면 → 그 결과로 x는 사라지고 y에 대한 식이 되니, y에 대해 정리하면 참값 y를 얻음. 얻은 y의 참값을 처음 x에 대해 정리한 1번식에 대입하면 참 값 x를 얻음. 구해진 참값의 근사값을 구하면 x=73.049507058547 and y=23.747548955927 어떤 solve로 나온 근사값이든, 근사값으로는 원래의 식 모두를 만족시킬 수 없음. 2025 10.21 그렇다면 해의 참 값은? 먼저, 모든 decimal 값을 유리수로 변환하고, solve 로 답을 구함. 변수 x로는 구해지는데 y로는 "Error: Resource exhaustion" 발생 // 이유는 모름. approx(exsol1) x=73.049507058547 and y=23.747548955927 2025 10.21 각 결과값의 비교 x y {x} 73.049507058553 23.747548955926 {y} 73.049507058479 23.747548955927 {x=1,y=1} 73.049507058477 23.747548955927 approx() 전처리 73.049507058479 23.747548955926 linsolve 73.049507058478 23.747548955926 approx(참 해) 73.049507058547 23.747548955927 * 구해진 x값들은 차이가 비교적 큰데, y값들은 차이가 적은 편입니다. 2025 10.21