- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
안티로그 Antilog 가 뭐지?? 첨 들어봤넹...
웹을 검색하다가 "안티로그"라는 단어를 처음 보게 되었습니다.

뭔가 로그에 대한 비난을 쏟아낼 것 같은 느낌이 들어서 움찔했는데,
그냥 '상용로그의 역함수'이더라구요.
(간혹 자연로그의 역함수로 설명하기도 합니다. 그냥 로그의 역함수로 보면 될 듯.)
![]() 괜히 쫄았네.ㅎ
괜히 쫄았네.ㅎ
"Antilog"는 수학에서 로그의 역연산을 의미합니다.
기본적으로 로그는 어떤 수가 특정한 밑에 대해 몇 번 곱해져서 다른 수가 되는지 찾는 과정입니다.
이때 antilog는 그 과정을 거꾸로 하는 작업으로, 주어진 로그 값으로부터 원래의 숫자를 구하는 것입니다.
예시
- 만약 우리가 \( \log_{10}(x) = 2 \)라는 값을 가지고 있다면, 이는 10을 몇 번 곱했을 때 \(x\)가 되는지 알려줍니다.
- \( \log_{10}(x) = 2 \)는 \( x = 10^2 \), 즉 \( x = 100 \)이 됨을 의미합니다.
- 이때 \(100\)을 "antilog"라고 부를 수 있습니다.
일반식
주어진 로그 값 \( y \)에 대해, 밑 \( b \)에 대한 antilog는 \( b^y \)입니다.
- 예를 들어, \( y = 3 \)이고 \( b = 2 \)인 경우, antilog는 \( 2^3 = 8 \)이 됩니다.
계산기에서 antilog 사용
일반 계산기에서는 보통 \(10^x\) 또는 \(e^x\) 키를 사용하여 10진수나 자연 로그의 antilog를 계산할 수 있습니다.
댓글4
-
세상의모든계산기
Logarithm Table (로그 테이블)
https://maths.forkids.education/antilog-log-table-how-to-use-see-value/
Download Print-Friendly PDF Version:
File 1 (1 to 50)
and
File 2 (51 to 99)
-
세상의모든계산기
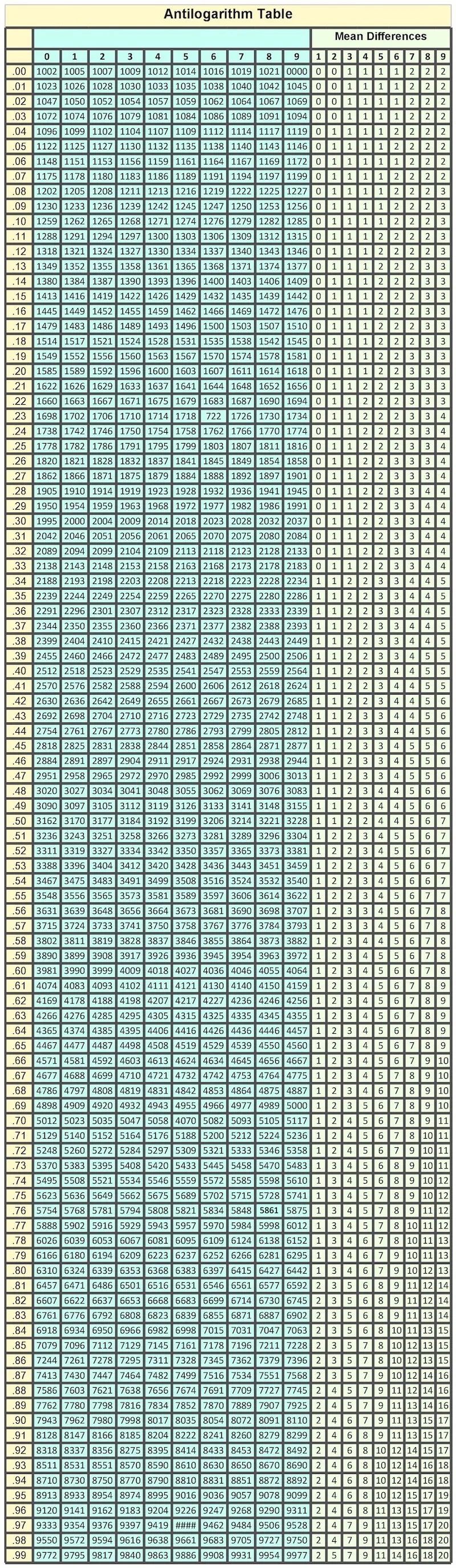
Antilogarithm Table (안티로그 테이블)
Download Print Friendly Antilog Table PDF File:
and
-
세상의모든계산기
log(k)= 1.5629228687415 에서 k 를 구할 때
말씀하신 내용을 반영하여 주어진 로그 값 \(\log_{10}(k) = 1.5629228687415\)에서 \(k\) 값을 정확하게 찾는 방법을 다시 설명드리겠습니다.
1. 정수 부분과 소수 부분 분리:
\[
\log_{10}(k) = 1.5629228687415
\]
여기서 정수 부분은 1이고, 소수 부분은 0.5629228687415입니다.2. 소수 부분을 두 자리로 반올림:
소수 부분 0.5629228687415을 두 자리로 반올림하면 0.56이 됩니다.3. 안티로그 표에서 0.56 찾기:
안티로그 표의 세로축에서 0.56을 찾습니다. 해당 행에서 첫 번째 열의 값은 3631입니다.
4. 소수 부분의 세 번째 자리 반영:
소수 부분의 세 번째 자리는 2입니다. 0.56 행의 두 번째 열(0.562에 해당)을 찾아야 합니다. 이 값은 3648입니다.5. 소수 부분의 네 번째 자리 반영:
소수 부분의 네 번째 자리는 9입니다. Mean Differences 열에서 9에 해당하는 값을 찾습니다. 이 값은 8입니다.6. 값 더하기:
안티로그 표의 0.562에 해당하는 값인 3648에 Mean Differences의 9에 해당하는 값 8을 더합니다:
3648 + 8 = 3656안티로그표의 값은 원래의 값을 1000배 한 값이므로, 원래값은 ÷1000 으로 구할 수 있습니다.
따라서 소수부분에 해당하는 값은 $ 10^{0.5629228687415} = 3.656 $ 입니다.
7. 정수 부분 반영:
\[
k = 10^{1.5629228687415} = 10^1 \times 10^{0.5629228687415}
\]정수 부분 1을 반영하기 위해 \(10^1\)을 곱합니다:
\[
k = 10^1 \times 3.656 = 10 \times 3.656 = 36.56
\]따라서 최종적으로 주어진 로그 값 \(\log_{10}(k) = 1.5629228687415\)에서 \(k\) 값을 구하면, \(k \approx 36.56\)이 됩니다.


세상의모든계산기 님의 최근 댓글
적용 사례 3 - 색상표 https://namu.wiki/w/%ED%97%A5%EC%8A%A4%20%EC%BD%94%EB%93%9C 적녹 색약 기준에서 필터 후 색깔을 느낌으로 표현하면 녹색 계열이 좀 차분? 묵직? 해지는 느낌 적색 계열이 전반적으로 조화를 이루지 못하고 튀는? 느낌 노랑이가 사라지는 느낌. * 적색 계열에서 글씨가 살짝 안보이는 것은 계조 문제(프로그램 문제)일 수 있겠다는 생각 2025 11.04 적용 사례 2 - 셔터스톡 https://www.shutterstock.com/ko/search/%EC%83%89%EC%95%BD%EA%B2%80%EC%82%AC?image_type=illustration 2025 11.04 적용 사례 1 - 본문 링크 중 2025 11.04 2번 사진 3개 사진 공통적으로 구석(corner) 에 증상이 있다는 특징이 있네요. 영상 찾아보니 이 가능성이 가장 높은 듯 합니다. https://www.youtube.com/watch?v=zxRBohepzwc ㄴ Liquid Crystal Leakage (액정 누설). ㄴ 손으로 밀어내니 주변으로 밀려나네요. 그래서 점으로 보이기도 하구요. 2025 10.29 500! 의 십진수 근사값 확인 500! = 1.22013682599111006870123878542304692625357434280319284219241358838 × 10^(1134) (참값, 울프람 알파) 2025 10.29