- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
안티로그 Antilog 가 뭐지?? 첨 들어봤넹...
웹을 검색하다가 "안티로그"라는 단어를 처음 보게 되었습니다.

뭔가 로그에 대한 비난을 쏟아낼 것 같은 느낌이 들어서 움찔했는데,
그냥 '상용로그의 역함수'이더라구요.
(간혹 자연로그의 역함수로 설명하기도 합니다. 그냥 로그의 역함수로 보면 될 듯.)
![]() 괜히 쫄았네.ㅎ
괜히 쫄았네.ㅎ
"Antilog"는 수학에서 로그의 역연산을 의미합니다.
기본적으로 로그는 어떤 수가 특정한 밑에 대해 몇 번 곱해져서 다른 수가 되는지 찾는 과정입니다.
이때 antilog는 그 과정을 거꾸로 하는 작업으로, 주어진 로그 값으로부터 원래의 숫자를 구하는 것입니다.
예시
- 만약 우리가 \( \log_{10}(x) = 2 \)라는 값을 가지고 있다면, 이는 10을 몇 번 곱했을 때 \(x\)가 되는지 알려줍니다.
- \( \log_{10}(x) = 2 \)는 \( x = 10^2 \), 즉 \( x = 100 \)이 됨을 의미합니다.
- 이때 \(100\)을 "antilog"라고 부를 수 있습니다.
일반식
주어진 로그 값 \( y \)에 대해, 밑 \( b \)에 대한 antilog는 \( b^y \)입니다.
- 예를 들어, \( y = 3 \)이고 \( b = 2 \)인 경우, antilog는 \( 2^3 = 8 \)이 됩니다.
계산기에서 antilog 사용
일반 계산기에서는 보통 \(10^x\) 또는 \(e^x\) 키를 사용하여 10진수나 자연 로그의 antilog를 계산할 수 있습니다.
댓글4
-
세상의모든계산기
Logarithm Table (로그 테이블)
https://maths.forkids.education/antilog-log-table-how-to-use-see-value/
Download Print-Friendly PDF Version:
File 1 (1 to 50)
and
File 2 (51 to 99)
-
세상의모든계산기
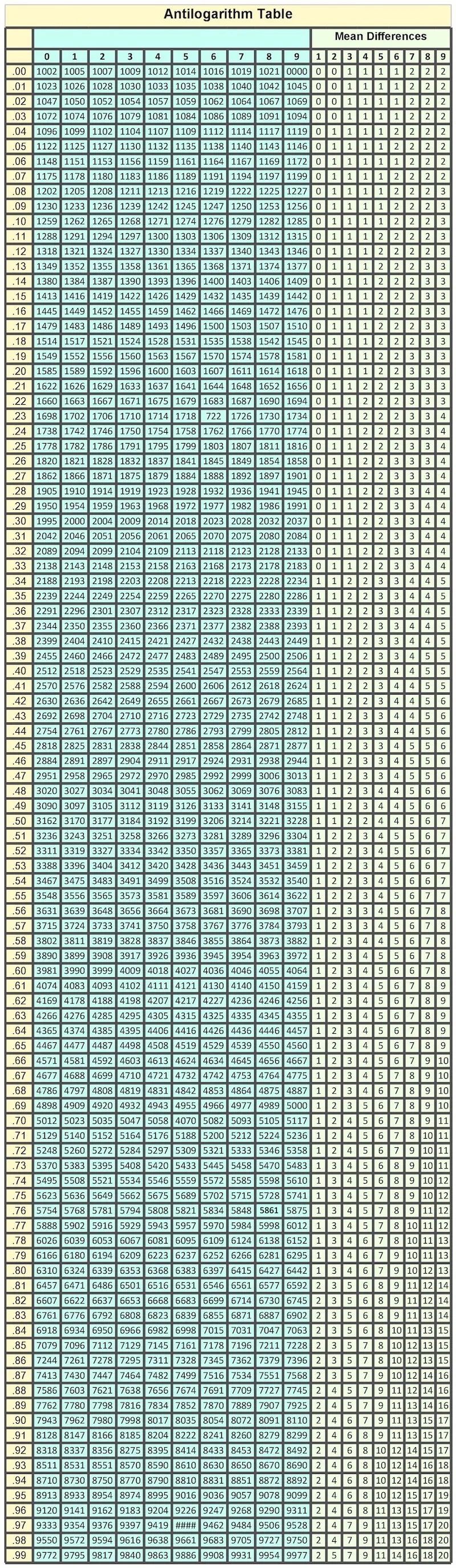
Antilogarithm Table (안티로그 테이블)
Download Print Friendly Antilog Table PDF File:
and
-
세상의모든계산기
log(k)= 1.5629228687415 에서 k 를 구할 때
말씀하신 내용을 반영하여 주어진 로그 값 \(\log_{10}(k) = 1.5629228687415\)에서 \(k\) 값을 정확하게 찾는 방법을 다시 설명드리겠습니다.
1. 정수 부분과 소수 부분 분리:
\[
\log_{10}(k) = 1.5629228687415
\]
여기서 정수 부분은 1이고, 소수 부분은 0.5629228687415입니다.2. 소수 부분을 두 자리로 반올림:
소수 부분 0.5629228687415을 두 자리로 반올림하면 0.56이 됩니다.3. 안티로그 표에서 0.56 찾기:
안티로그 표의 세로축에서 0.56을 찾습니다. 해당 행에서 첫 번째 열의 값은 3631입니다.
4. 소수 부분의 세 번째 자리 반영:
소수 부분의 세 번째 자리는 2입니다. 0.56 행의 두 번째 열(0.562에 해당)을 찾아야 합니다. 이 값은 3648입니다.5. 소수 부분의 네 번째 자리 반영:
소수 부분의 네 번째 자리는 9입니다. Mean Differences 열에서 9에 해당하는 값을 찾습니다. 이 값은 8입니다.6. 값 더하기:
안티로그 표의 0.562에 해당하는 값인 3648에 Mean Differences의 9에 해당하는 값 8을 더합니다:
3648 + 8 = 3656안티로그표의 값은 원래의 값을 1000배 한 값이므로, 원래값은 ÷1000 으로 구할 수 있습니다.
따라서 소수부분에 해당하는 값은 $ 10^{0.5629228687415} = 3.656 $ 입니다.
7. 정수 부분 반영:
\[
k = 10^{1.5629228687415} = 10^1 \times 10^{0.5629228687415}
\]정수 부분 1을 반영하기 위해 \(10^1\)을 곱합니다:
\[
k = 10^1 \times 3.656 = 10 \times 3.656 = 36.56
\]따라서 최종적으로 주어진 로그 값 \(\log_{10}(k) = 1.5629228687415\)에서 \(k\) 값을 구하면, \(k \approx 36.56\)이 됩니다.


세상의모든계산기 님의 최근 댓글
fx-570 CW 는 아래 링크에서 https://allcalc.org/56026 2025 10.24 불러오기 할 때 변수값을 먼저 확인하고 싶을 때는 VARIABLE 버튼 【⇄[x]】목록에서 확인하고 Recall 하시면 되고, 변수값을 이미 알고 있을 때는 바로 【⬆️SHIFT】【4】로 (A)를 바로 입력할 수 있습니다. 2025 10.24 fx-570 CW 로 계산하면? - 최종 확인된 결과 값 = 73.049507058478629343538 (23-digits) - 오차 = 6.632809104889414877 × 10^-19 꽤 정밀하게 나온건 맞는데, 시뮬레이션상의 22-digits 와 오차 수준이 비슷함. 왜 그런지는 모르겠음. - 계산기중 정밀도가 높은 편인 HP Prime CAS모드와 비교해도 월등한 정밀도 값을 가짐. 2025 10.24 HP Prime 에서 <Home> 73.0495070344 (12-decimal-digits) // python 시뮬레이션과 일치 <CAS> 21자리까지 나와서 이상하다 싶었는데, Ans- 에서 자릿수를 더 늘려서 빼보니, 뒷부분 숫자가 아예 바뀌어버림. 버그인가? (전) 73.0495070584718691243 (21-digits ????) (후) 73.0495070584718500814401 (24-digits ????) 찾아보니 버그는 아니고, CAS에서는 십진수가 아니라 2진수(bit) 단위로 처리한다고 함. Giac uses 48 bits mantissa from the 53 bits from IEEE double. The reason is that Giac stores CAS data (gen type) in 64 bits and 5 bits are used for the data type (24 types are available). We therefore loose 5 bits (the 5 low bits are reset to 0 when a double is retrieved from a gen). 출처 : https://www.hpmuseum.org/cgi-bin/archv021.cgi?read=255657 일단 오차를 놓고 보면 16-decimal-digits 수준으로 보임. 2025 10.23 khiCAS 에서 HP 39gII 에 올린 khiCAS는 254! 까지 계산 가능, 255! 부터는 ∞ fx-9750GIII 에 올린 khiCAS는 factorial(533) => 425760136423128437▷ // 정답, 10진수 1224자리 factorial(534) => Object too large 2025 10.23