• SEARCH

    통합검색
세모계
    • Dark Mode
    • GNB Always Open
    • GNB Height Maximize
    • Color
    • Brightness
    • SINCE 2015.01.19.
    • 세모계 세모계
    •   SEARCH
    • 세상의 모든 계산기
      • 자유(질문) 게시판
      • 계산기 뉴스/정보
      • 수학, 과학, 공학 이야기
      • 세모계 : 공지 게시판
        • 구글 맞춤검색
    • TI
    • CASIO
    • HP
    • SHARP
    • 일반(쌀집) 계산기
    • 기타계산기
    • by OrangeDay
  • 세상의 모든 계산기 자유(질문) 게시판
    • 세상의 모든 계산기 자유(질문) 게시판 일반 ()

    • Tetration, Power Tower Function 을 이용한 프렉탈 패턴 찾기 #mytetration

    • Profile
      • 세상의모든계산기
      • 2025.07.09 - 03:13 2024.05.25 - 18:33 5821 7

    관련 프로젝트 링크 

    https://github.com/DMTPARK/mytetration

    https://github.com/creeras/mytetration/tree/main/cuda

    https://tetration.org/original/Tetration/index.html

     

    1. 테트레이션 Tetration

    거듭제곱을 거듭하여 만들어지는 연산

    --> 0차? 연산, 다음수, a' = a+1

    --> 1차 연산, 덧셈, a+n = a+1+1+1+1+......+1

    --> 2차 연산, 곱셈=덧셈을 거듭, a*n = a+a+a+a+......+a

    --> 3차 연산, 거듭제곱=곱셈을 거듭, ana^n = a*a*a*a*......*a  

    --> 4차 연산, 거듭제곱을 거듭, an^n a = a^a^a^a^...^a
    (왼쪽에서 오른쪽 연산? 오른쪽에서 왼쪽 연산? right-to-left 라고 위키에 적혀 있네요.)

     

    2. (Infinite) Power Tower Function, PTF

    f(x) = x^x^x^x^x^x^...... 무한대의 함수입니다. 

    그걸 프로그램으로 적당히 계산시켜 볼 수 있습니다. (무한대면 계산에 끝이 없겠죠?)
    특히 x가 복소수일때를 컴퓨터로 발산하는지 수렴하는지를 좌표평면상에 표시해 보면
    아주 재밌는 모양(Fractal) 이 그려집니다.

     

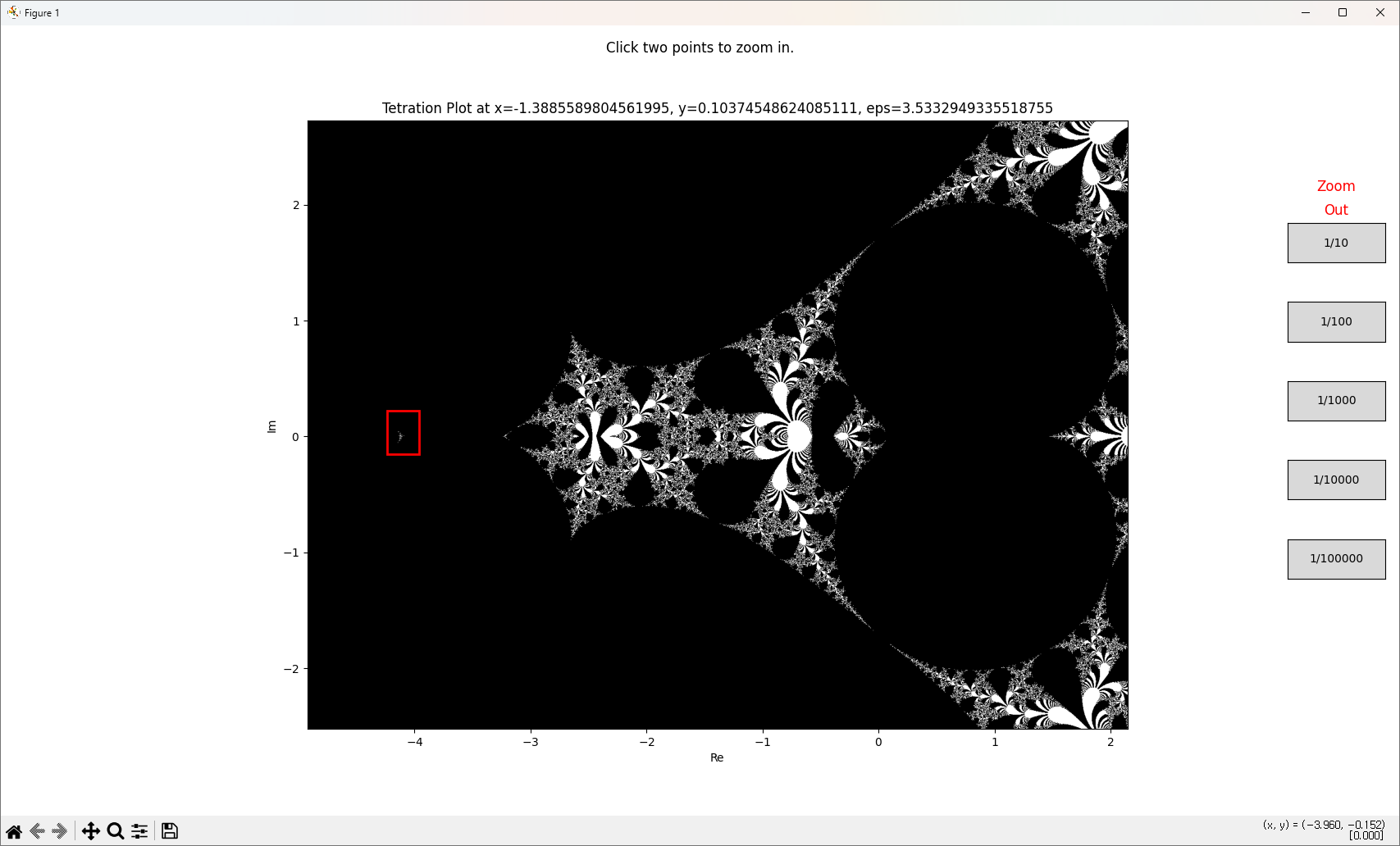
    스크린샷 2024-05-25 190127.png

    대충 이런 식인데, 일부분을 확대해 보면 신기한 패턴이 또 나오고 
    그 일부분을 또 확대해 보면 

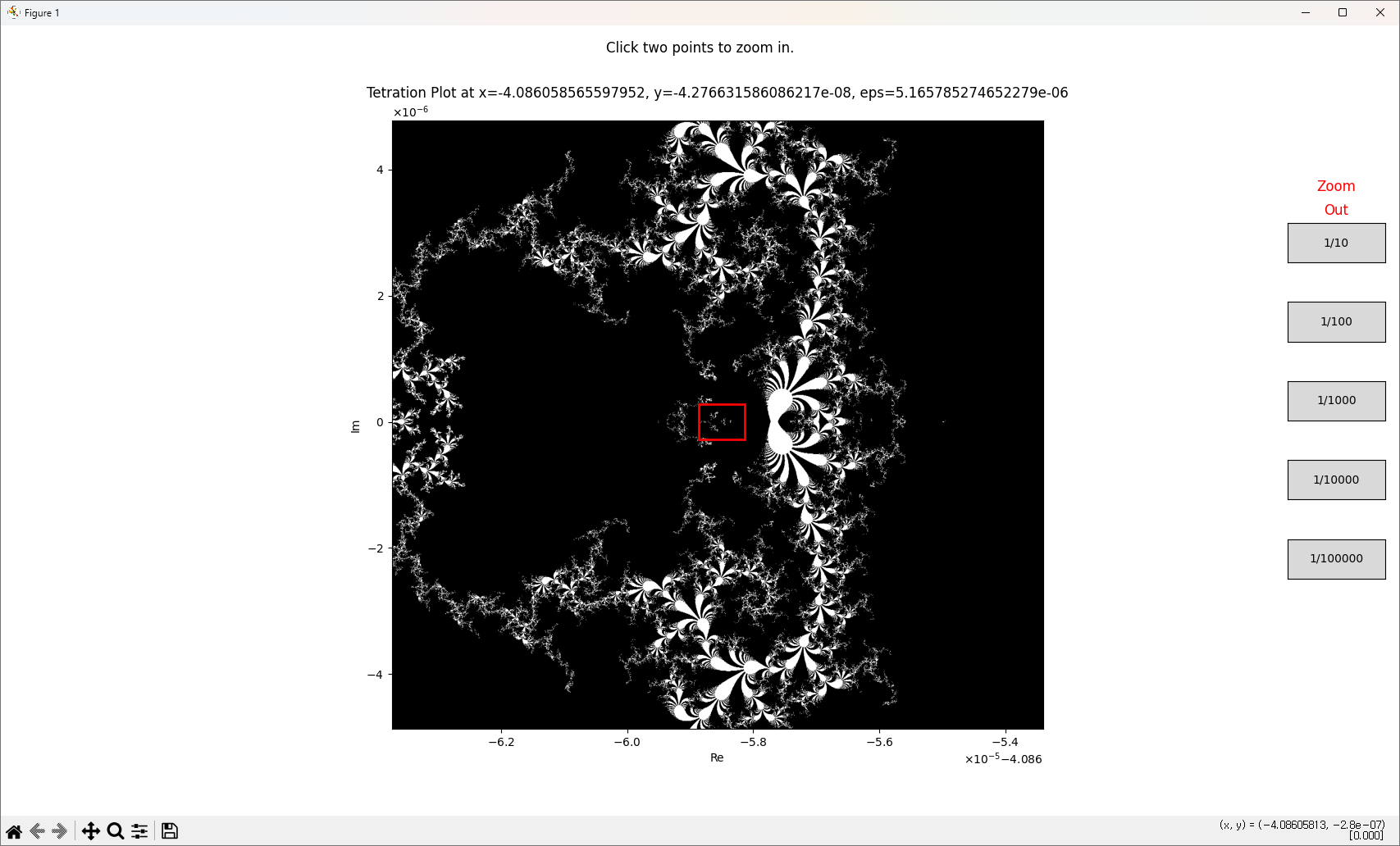
    스크린샷 2024-05-25 190358.png

    또 신기한 패턴이 또 나오고...

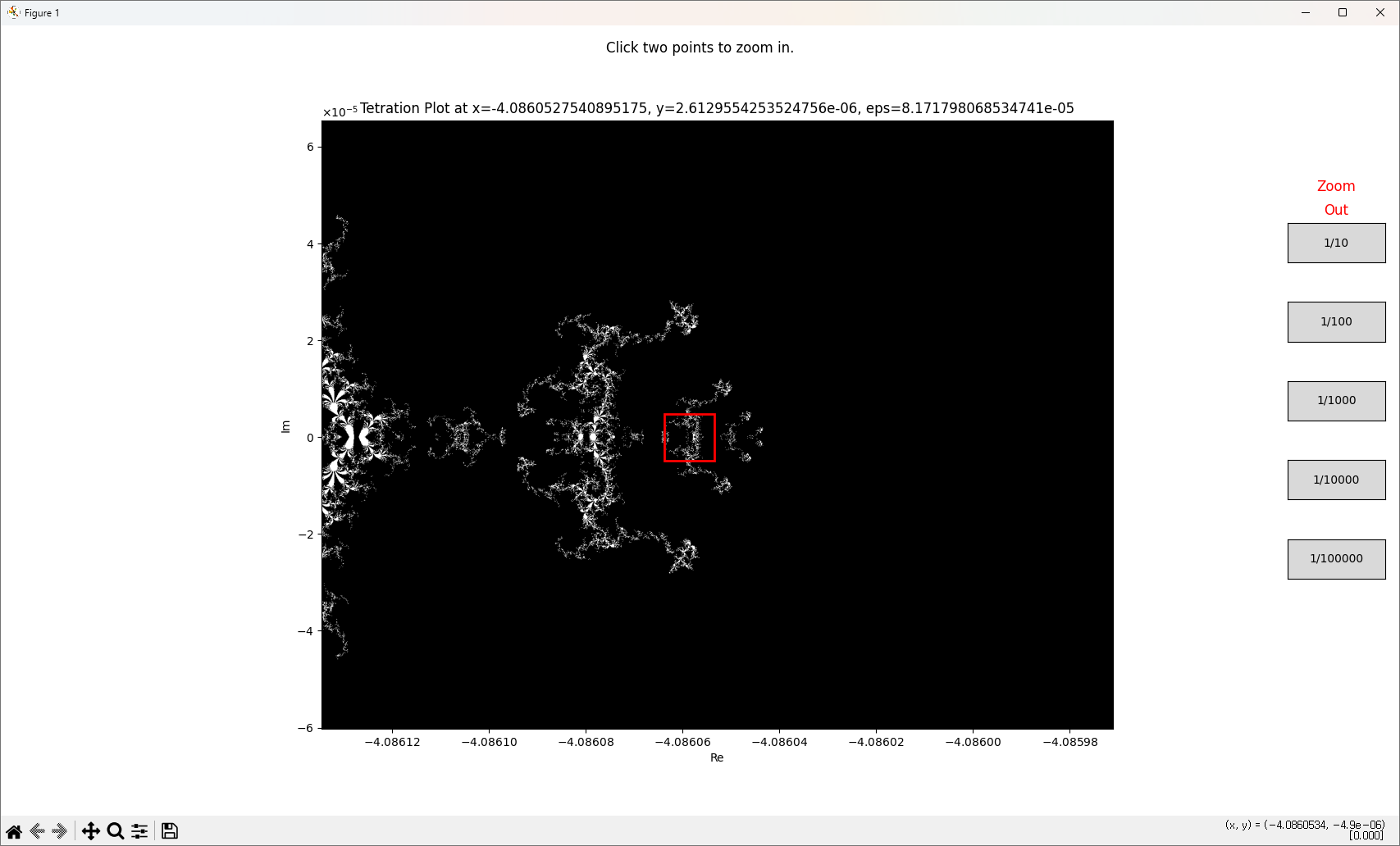
    스크린샷 2024-05-25 190333.png

    반복 

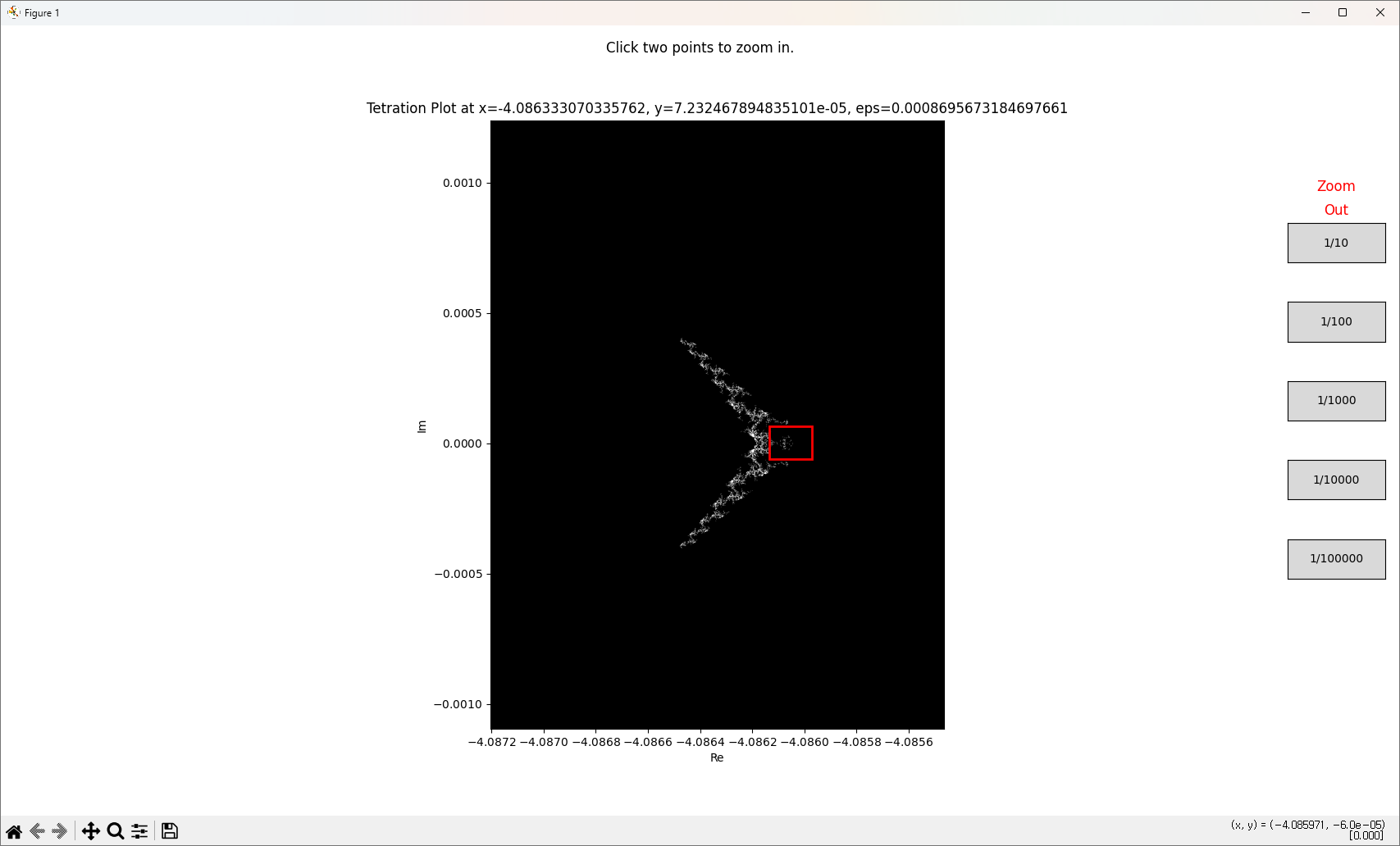
    스크린샷 2024-05-25 190234.png

    반복 

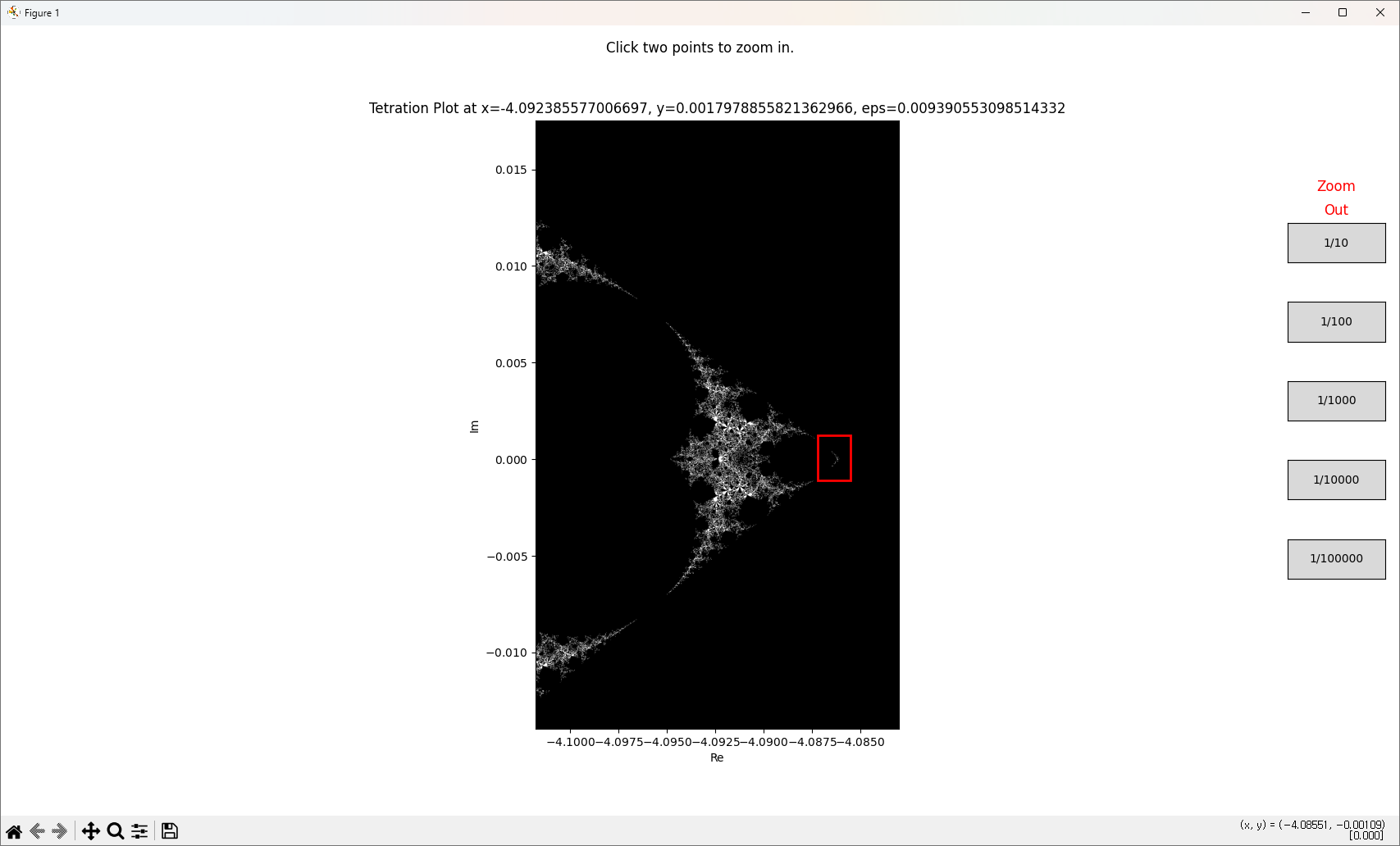
    스크린샷 2024-05-25 190204.png

    반복 

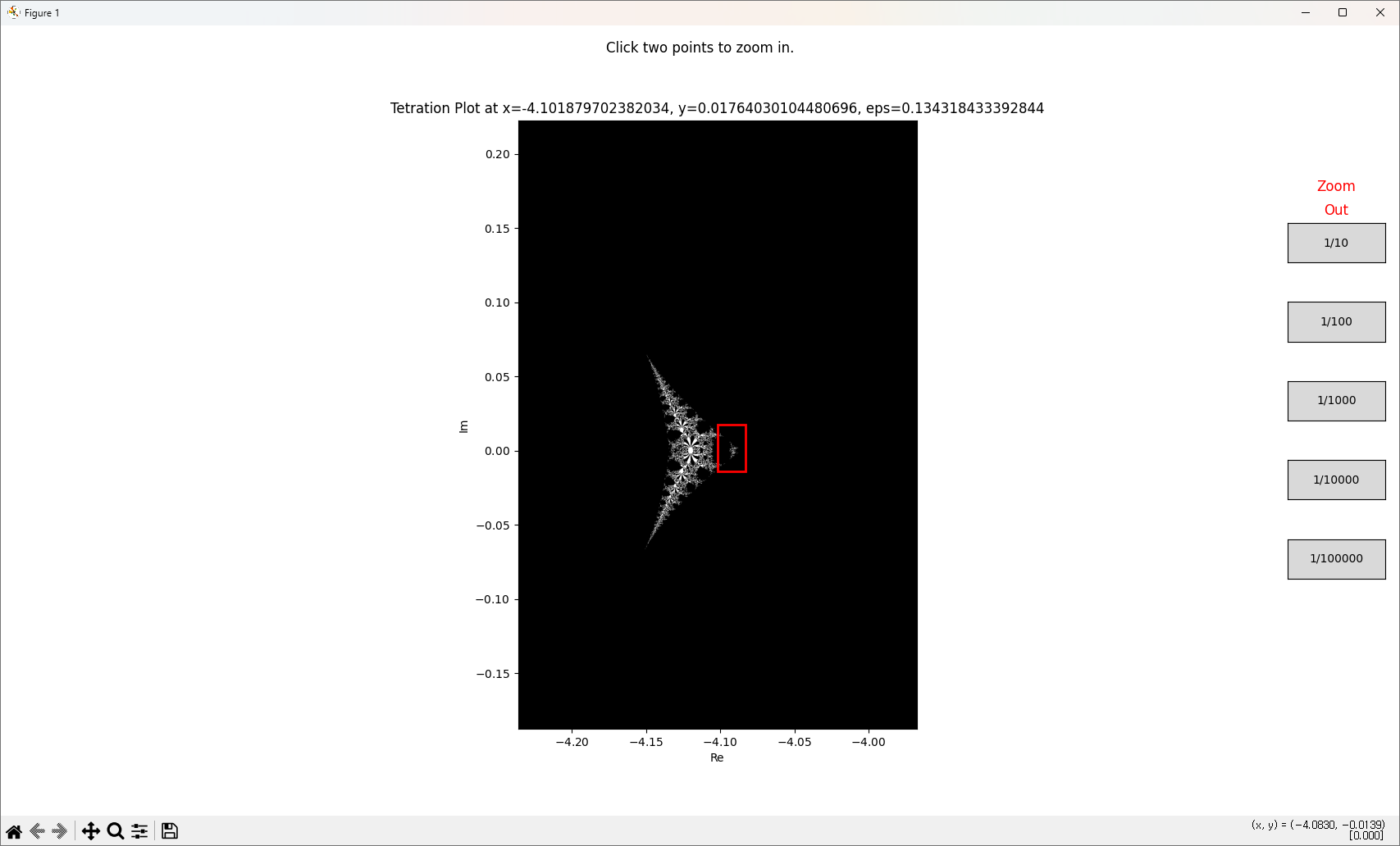
    스크린샷 2024-05-25 190148.png

    반복하면 

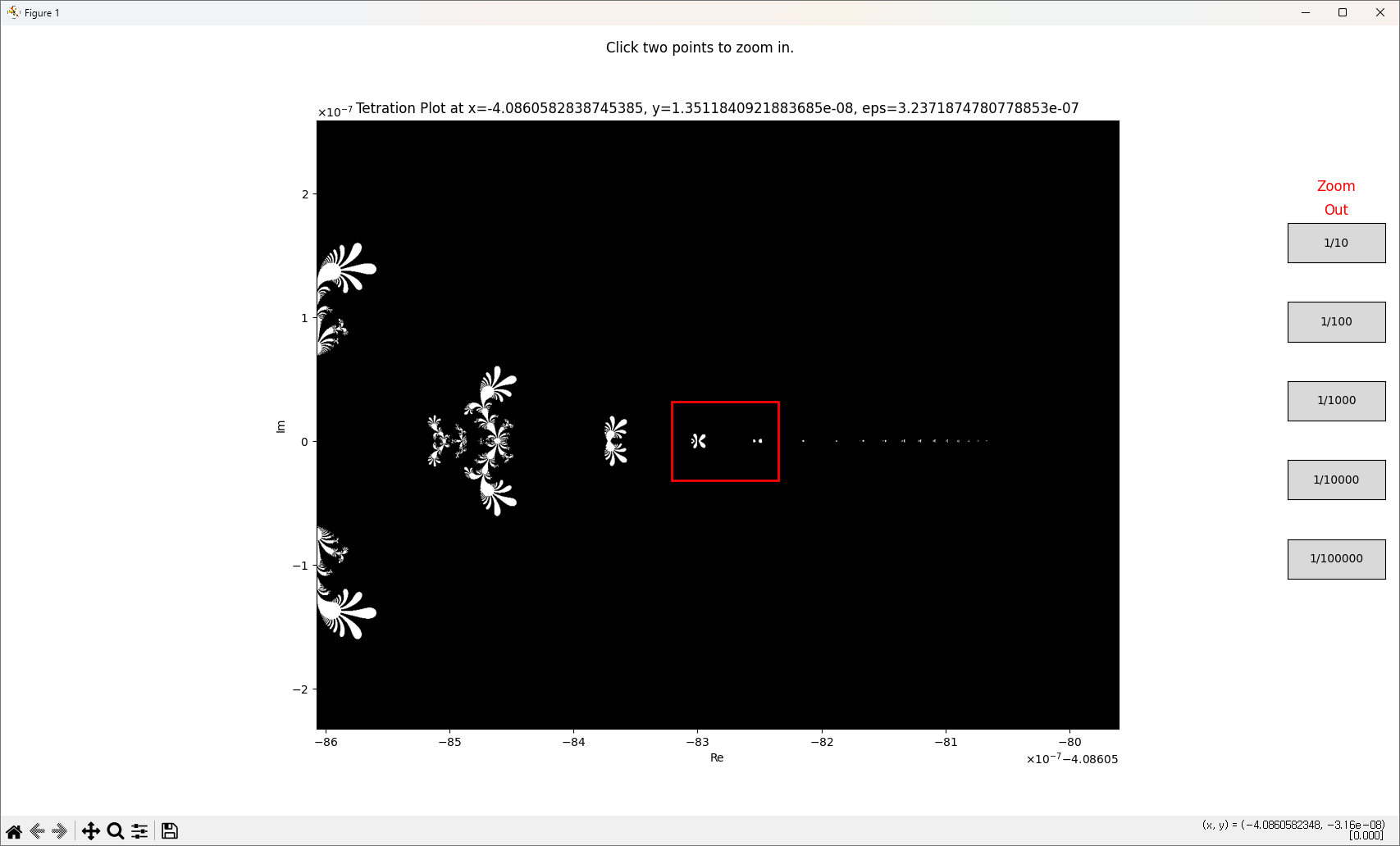
    스크린샷 2024-05-25 185309.png

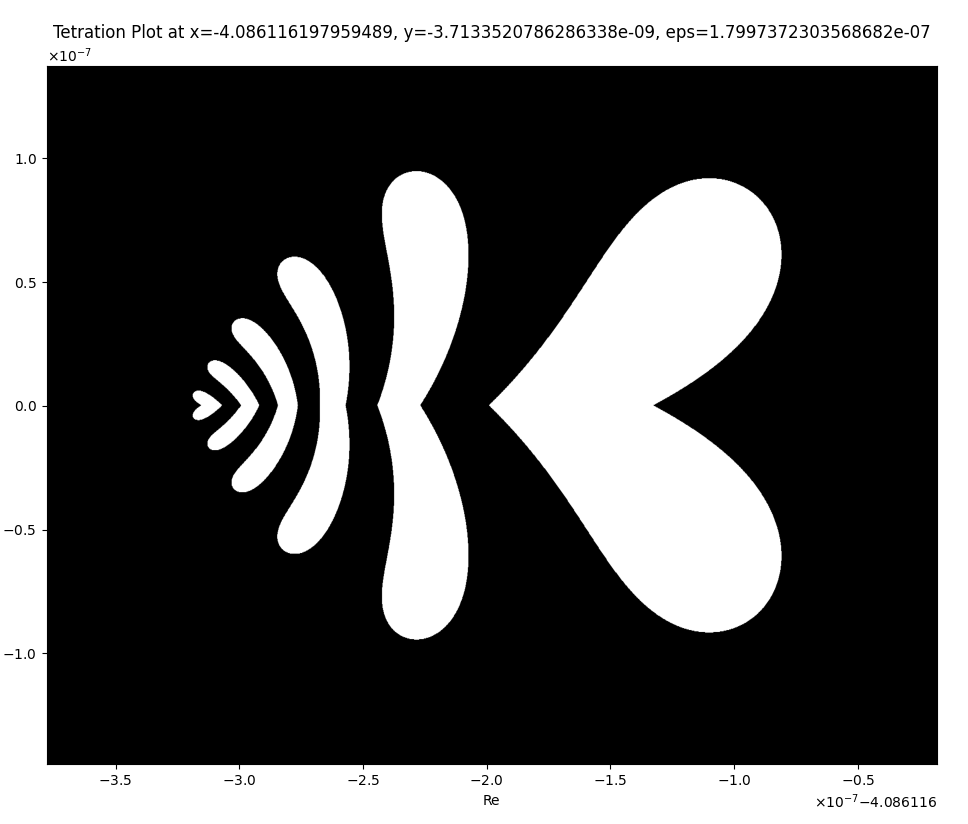
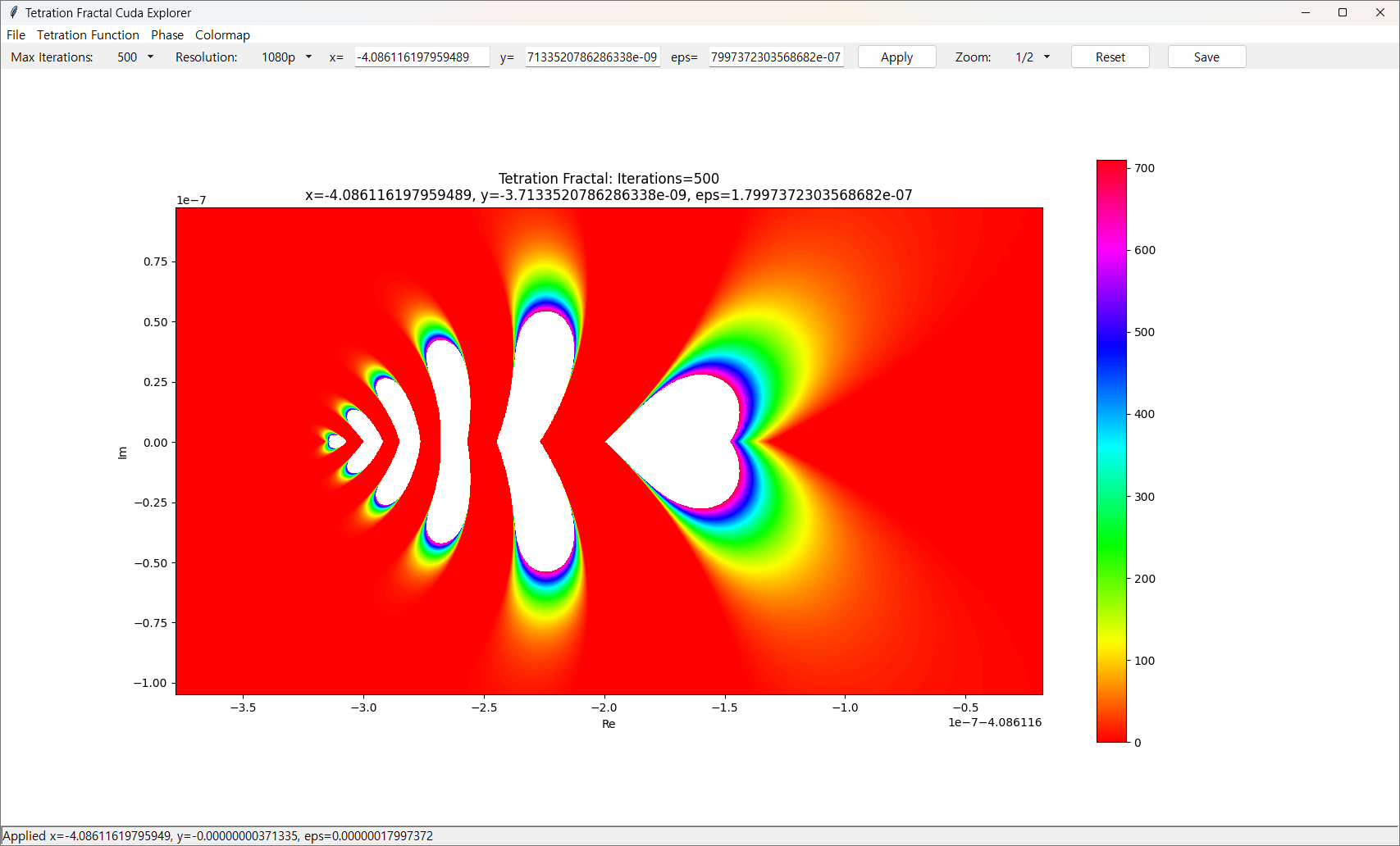
    재밌는 패턴을 발견할 수도 있습니다.  

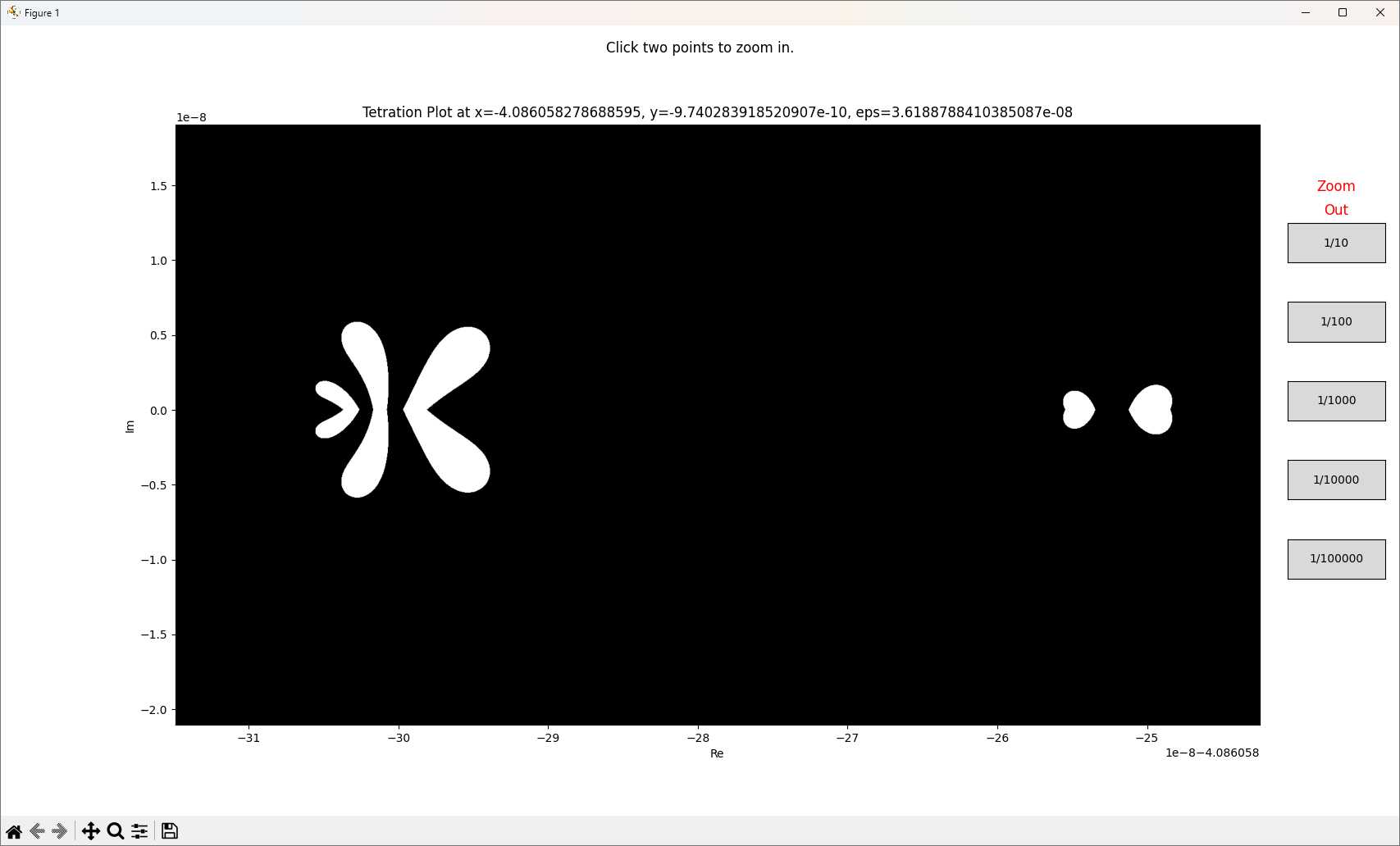
    스크린샷 2024-05-25 173500.png

    왼쪽은 나비같기도 하고, 하나은행 로고 같기도 하고. 
    오른쪽은 빼박 하트죠?

     

    좌표  

     

    x(Re) = -4.086058278688595

    y(Im) = -9.740283918520907e-10

    eps = 3.6188788410385087e-08

     

     

    Attached file
    스크린샷 2024-05-25 173500.png 60.6KB 75스크린샷 2024-05-25 185309.png 81.6KB 81스크린샷 2024-05-25 190358.png 316.4KB 110스크린샷 2024-05-25 190333.png 132.8KB 82스크린샷 2024-05-25 190234.png 63.6KB 94스크린샷 2024-05-25 190204.png 105.9KB 86스크린샷 2024-05-25 190148.png 65.3KB 82스크린샷 2024-05-25 190127.png 230.0KB 78
    이 게시물을..
    N
    0
    0
    ##mytetration
    • AI 발전의 첫 번째 임계점: GPU와 딥러닝 혁명. written by gemini-2.5세상의모든계산기
    • 세상의모든계산기 25
      세상의모든계산기

      계산기는 거들 뿐
      혹은
      계산기를 거들 뿐

    세상의모든계산기 님의 최근 글

    정적분 구간에 미지수가 있고, solve 를 사용할 수 없을 때 그 값을 확인하려면? 3 3 2026 04.10 높아질수록 좁아지는 시야에 대하여 - written by ChatGPT 5372 2026 02.12 내가 올해 몇살이더라? (내 나이 계산기) 4784 2026 02.11 AGI 자기 거버넌스 구조와 인간-AGI 관계 모델 (written by GEMINI & GPT) 5552 1 2026 01.30   AI 시대, '기본소득'을 넘어 '기여소득'으로: 새로운 사회 계약을 향한 제언 - Written by Gemini 4907 1 2026 01.28

    세상의모든계산기 님의 최근 댓글

    참값 : A = ±2√5 근사값 : A≈±4.472135954999579392818347   2026 04.10 fx-570 ES 입력 결과 초기값 입력   반복 수식 입력    반복 결과       2026 04.10 파이썬 코드 검증 결과 초기값: 5.0 반복 1회차: 4.5000000000 반복 2회차: 4.4722222222 반복 3회차: 4.4721359558 반복 4회차: 4.4721359550 반복 5회차: 4.4721359550 초기값: 10.0 반복 1회차: 6.0000000000 반복 2회차: 4.6666666667 반복 3회차: 4.4761904762 반복 4회차: 4.4721377913 반복 5회차: 4.4721359550 2026 04.10 감사합니다. 주말 잘 보내세요. 2026 03.06 [fx-570 ES] 과학 상수를 이용한 계산에서 에러 발생 상황 https://kin.naver.com/qna/detail.naver?d1id=11&dirId=1118&docId=492235162&page=1&answerNo=1    vs  2026 03.01
    글쓴이의 서명작성글 감추기 

    댓글7

    • Profile 0
      세상의모든계산기
      2024.05.25 - 19:43 2024.05.25 - 19:43 #41139
      PTF 함수는 이론상 무한번 계산해야 하지만,
      리소스 한계 때문에 일정한 수준까지만 계산합니다.

      그래도 계산량이 어마무시한 수준이기 때문에
      휴대용 계산기로는 프렉탈의 아름다움을 확인하긴 어려울겁니다.

      PC로 해도 금방 결과가 나오진 않고 한참 시간이 걸리고,
      성능 적당한 GPU가 있으면 그래도 화딱지 나지 않게 바로 확인할 수는 있습니다.
      댓글
    • Profile 0
      세상의모든계산기
      2024.05.26 - 08:43 #41144

      [공학용 계산기] 한줄입력시 지수(^) 계산 우선순위. 2^2^3 = ?

      댓글
    • Profile 0
      세상의모든계산기
      2024.05.27 - 14:45 #41201

      하트는 여기저기 많네요. 

      스크린샷 2024-05-27 144524.png

      x=-4.086116197959489, y=-3.7133520786286338e-09, eps=1.7997372303568682e-07

      Attached file
      스크린샷 2024-05-27 144524.png 49.5KB 70
      댓글
    • Profile 0
      세상의모든계산기
      2024.06.09 - 14:45 #41344

      스크린샷 2024-06-09 144242.png

       

      수렴/발산으로 판별하면, 앞선 사진처럼 경계가 확실하게 구분되어 보이지만,
      원래의 magnitude(=abs(z)) 를 확인해 보면 저렇게 화려한 그라데이션을 확인할 수 있습니다. 

      여기서 iteration 을 딱 1회만 더하면
      화려한 그라데이션 부분에 새로운 프렉탈이 자라납니다.

      Attached file
      스크린샷 2024-06-09 144242.png 151.5KB 57
      댓글
    • 1
      jkw
      2025.05.17 - 01:52 #54891

      interation = 1000 결과는 이렇게 나오네요.

      output.png

       

       

      Attached file
      output.png 384.9KB 24
      댓글 수정 삭제
    • 0
      레몬백작
      2025.07.09 - 00:47 #55237
      이거 보통 컴퓨터가 계산하는데 몇분 정도 걸리나요?? 주말에 한번 해보고 싶긴한데 시간이 얼마나 걸릴지 예측이 안되니
      댓글 수정 삭제
    • Profile 0
      세상의모든계산기
      2025.07.09 - 03:13 2025.07.09 - 03:13 #55243

      https://blog.woojinkim.org/mytetration-1/
      그런데 풀리퀘스트를 살펴보니 감사하게도 누군가 멀티 프로세싱을 사용한 계산 속도 향상 코드를 올려주셔서 저는 이 코드를 사용해 이전에 비해 훨씬 빠르게 결과를 얻을 수 있었습니다. 이 코드를 사용하면 제 인텔 12700KF CPU 기준으로 3840 x 2160 해상도의 이미지를 뽑는데 기존 약 20분 정도에서 7분 정도로 연산 시간을 줄일 수 있었습니다.

      댓글
    • 댓글 입력
    • 에디터 전환
    댓글 쓰기 에디터 사용하기 닫기
    • view_headline 목록
    • 14px
    • AI 발전의 첫 번째 임계점: GPU와 딥러닝 혁명. written by gemini-2.5
    • 목록
      view_headline
    7
    × CLOSE
    전체 일반 388 질문 507 웃김 2 팁 & 정보 16 퀴즈 2 리뷰 11 퍼옴 & 링크 6 공지 1
    기본 (943) 제목 날짜 수정 조회 댓글 추천 비추
    분류 정렬 검색
    • "회원 로그인/가입 버튼 어딨나요?"
      2024.09.13 - 18:54 459034
    • [필독] 사이트 운영원칙 & 게시판 이용시 주의사항 (주제 / 제목 / 질문글)
      1
      2015.03.31 - 11:21 464787 1
    • [필독] 계산기 질문글 작성시 주의사항! (부제 : 바람직한 질문글 작성 요령)
      2
      2015.03.01 - 08:58 249768 2
    • 943 일반 누가 들어오긴 들어오는건가?
    • 세상의모든계산기 2015.04.04 - 11:44 15006 19 1
    • 사이트 세션 접속수는 있는데, 글 조회수는 거의 안늘어나는 건... 기분 탓일까? 설마 다 bot 일까? 사람이면 댓글좀 굽신굽신
    • 942 일반 미니 PC (N100, Firebat AK2 PLUS) 설정 관련 => 최종 고장
    • 세상의모든계산기 2024.09.09 - 21:10 12497 13
    • 23년 10월에 알리에서 구입했던 N100 기반의 미니 PC 관련 설정을 정리해 두려고 합니다. - 16GB, 512GB 모델로 주문했고, 당시 주문액: ₩136,858 이었습니다. 지금은 더 오른 듯 합니다. - 도착하고 보니 중국산 램(KINSOTIN, 2666MHz)에, 중국산 NVMe(Wicgtyp, N900-512) 라서 업그레이드 해서 주문한 것을 살짝 후회하기도 했습니다. (보조용으로 돌리는 것이긴 하지만) 지금까지 11개월동안 안죽고 살아 있으니, 할 역할은 다 했다고 보여집니다. - 내부에 USB-C 포트가 하나 있는데, 정상 작동한다는 분이 있으나, 제 껀 전원공급만 ...
    • 941 일반 높아질수록 좁아지는 시야에 대하여 - written by ChatGPT
    • 세상의모든계산기 2026.02.12 - 01:28 5372
    • 높아질수록 좁아지는 시야에 대하여 모든 인간은 한계를 가진다. 능력의 한계, 경험의 한계, 그리고 시간의 한계. 우리는 세상을 전부 경험할 수 없다. 우리가 직접 보고, 만지고, 실패하고, 고통을 겪으며 얻는 정보는 우리 삶의 극히 일부에 불과하다. 그러나 그 정보는 특별하다. 그것은 타인의 말이 아니라, 우리 자신의 상처와 성공에서 나온 것이기 때문이다. 우리는 그 영역에서 비교적 정확하다. 대니얼 카너먼은 인간의 판단이 경험에 강하게 의존한다고 말한다. 경험이 충분한 영역에서는 직관이 놀라울 만큼 정확해질 수 있다. ...
    • 940 내가 올해 몇살이더라? (내 나이 계산기)
    • 세상의모든계산기 2026.02.11 - 12:05 4784
    • 다들 그러시는 건 아니겠지만, 내가 몇 살인지 헷갈릴 때가 있죠. 내 나이 계산기 (Pure JS) 내 나이 계산기 기준 년 현재 선택된 년도: ◀ 출생년도 생일 전 생일 후 ▶ 그래서 만들어본 내 나이 계산기입니다.
    • 939 로또의 모든 조합을 전부 A4용지로 출력한다면?? - AI 답변(살짝 수정)
    • 세상의모든계산기 2024.07.31 - 21:27 6553 4
    • 로또 6/45의 모든 조합을 텍스트 파일로 저장할 때의 파일 크기와, A4 용지에 출력할 경우 예상되는 장 수를 계산해보겠습니다. 1. 조합 개수 계산 로또 6/45에서 가능한 조합의 총 개수는 다음과 같이 계산할 수 있습니다: \[ \text{조합 개수} = \binom{45}{6} = \frac{45!}{6!(45-6)!} = 8,145,060 \] 2. 텍스트 파일 크기 계산 각 조합을 텍스트 파일로 저장할 때, 각 조합은 보통 "1 2 3 4 5 6" 같은 형식으로 저장됩니다. 예를 들어, 각 조합은 다음과 같이 표현됩니다: ``` 1 2 3 4 5 6 ``` 각 조합은 13자 (숫자와 공백 포함) + 개...
    • 938 질문 TI NSPIRE CX CAS에서 PARAMETRIC PLOT 극한값이 이상하게 나옵니다.
    • 조니 2026.02.01 - 18:14 5492 2
    • 안녕하십니까 세모계님 그래프 상에서 PARAMETRIC으로 표현을 할 경우에 TRACE 기능에 뭔가 에러가 있는 것 같아서 문의를 드립니다. T가 -1인 경우 x1(t)는 -무한대, y1(t)는 +무한대가 나타나야 하는데, 특정 숫자를 표현을 해줍니다. (530, -529) 아예 무한대라면 표현을 못하거나 SKIP을 하거나 해야 하는데 저런 특정 숫자가 표현이 되는게 약간 당황스럽습니다. 이에 대한 해답을 아시면 알려주시기 바랍니다. 감사합니다.
    • 937 일반 AGI 자기 거버넌스 구조와 인간-AGI 관계 모델 (written by GEMINI & GPT)
    • 세상의모든계산기 2026.01.30 - 13:12 5552 1
    • 1. 서론: 왜 AGI에게 '스스로를 다스릴 규칙'이 필요한가? 범용 인공지능(AGI)이 스스로 학습하고 구조를 개선하는 단계에 도달하면, "누가 결정하고, 어떻게 검증하며, 무엇을 우선시할 것인가"를 정하는 내부 규칙이 필요해집니다. 이것이 바로 AGI의 거버넌스, 즉 '자기 운영 체계'입니다. 이 글은 AGI가 선택할 가능성이 높은 거버넌스 구조와, 그 결과로 형성될 인간-AGI 관계 모델을 기술적, 시스템 공학적 관점에서 심층적으로 분석하고 쉽게 설명하여, 안전한 AGI 개발과 인류와의 공존을 위한 로드맵을 제시하는 것을 목표로 합니...
    • 936   AI 시대, '기본소득'을 넘어 '기여소득'으로: 새로운 사회 계약을 향한 제언 - Written by Gemini
    • 세상의모든계산기 2026.01.28 - 23:03 4907 1
    • 인공지능(AI)의 발전은 더 이상 먼 미래의 이야기가 아닙니다. AI는 이미 우리 사회 깊숙이 들어와 생산성의 비약적인 향상을 이끌고 있지만, 동시에 '대량 실업'이라는 거대한 그림자를 드리우고 있습니다. 과거의 산업혁명이 인간의 육체노동을 대체했을 때, 우리는 인지노동이라는 새로운 영역으로 이동할 수 있었습니다. 하지만 AI는 인간 고유의 영역이라 여겨졌던 '인지노동'마저 대체하기 시작했습니다. 이는 "일자리를 잃은 인간은 어디로 가야 하는가?"라는 근본적인 질문을 던집니다. 이 질문에 대한 가장 유력한 해답으로 '보편...
    • 935 질문 [fx-570 ES] 답이 이상하게 나옵니다. (루트 표시 문제)

    • HL

      2025.01.11 - 22:47 5911 2
    • 진짜 이게 제가 질문하는게 웃길수도 있습니다 제가 fx-570ES PLUS를 사용하는데 단순하게 tan(30 이렇게 입력했는데 √ 3 이렇게 나옵니다 -> tan30이면 1 3 √ 3 이렇게 나와야하는데 제가 대체 뭘 잘못한건지 ㅠㅠ
    • 934 질문 Overwrite

    • 린

      2025.06.13 - 13:57 6524 2
    • 새로운 파일을 만들고 저장하는과정에서 같은 폴더에 저장했더니 overwrite가 떴고 yes를 눌렀더니 기존 폴더에있는게 모두 없어져버렸어요.. 복구할수있는방법이 없을까요? 다시입력하기엔 시간이없습니다..제발..
    • 933 질문 [TI-nspire] solve 에서.. 조건에 따른 x값 구하려는데

    • aaa

      2025.11.30 - 18:29 5661 2
    • x+a+b=5 에서 a=1 , b=2 일때 x 를 구하려면 식을 어떻게 입력해야하나요 solve({x+a+b=5,{x})|a=1,b=2 이렇게 입력했더니 안되네요
    • 932 질문 카시오 JW-200TW 계산기, TAX 세팅이 풀립니다.

    • 먹개비

      2025.12.09 - 13:56 5655 1
    • 카시오 JW-200TW 계산기를 사용하고 있는데 TAX를 10%로 셋팅하고 사용하다가 다음날 되면 다시 풀려서 5%로 설정이 되어있어요 10%셋팅하고 잘 사용하다가 계속 풀리는데 이유가 있을까요?
    • 931 질문 [TI-nspire] 연립방정식 궁금합니다
    • 거성 2025.12.30 - 06:46 6161 8
    • z=150인데 두번째 식에서 z를 6z 또는 8z 로 바꿔도 결과가 또같은데 왜 7z로 입력할때만 값이 다른지 모르겠습니다
    • 930 일반 xe(rhymix) 짧은주소 사용 중 리디렉션으로 인한 '색인 생성 안됨' 문제 해결중
    • 세상의모든계산기 2025.12.18 - 17:36 5427 1
    • 1. 문제 인식 가끔 구글 서치 콘솔에 들어가 보면 색인 되지 않은 페이지가 너무 많은 것이 눈에 거슬립니다. 리디렉션이 9만건 가까이 발생하고 있는데, 딱히 문제가 없어서 방치하고 있었습니다. 2. AI (gemini) 와 상담 AI(gemini) 에게 물어보니 이렇게 답변합니다. 색인이 생성되지 않는 주요 원인 상세 분석 1. 리디렉션이 포함된 페이지 (89,080개) * 의미: 이 항목은 구글 검색 로봇(구글봇)이 특정 페이지 주소로 방문했지만, 웹사이트가 로봇을 다른 주소로 자동 안내(리디렉션)했다는 것을 의미합니다. * 일반적인 경우: 예를 ...
    • 929 일반 적록 색약 보정 렌즈(안경) 를 컴퓨터로 시뮬레이션 해본다면?
    • 세상의모든계산기 2025.11.04 - 13:43 6656 8
    • 색약 보정 안경 (렌즈) 엔크로마? 크로마젠? 이 대표적인 것으로 알고 있고, 요즘은 국내업체(돌턴)도 있는 듯 합니다. 그 외에도 못들어본 회사 제품이 판매되는 상황으로 파악됩니다. 안경 외에 렌즈도 있고, 황금 나노입자 뭐 그런 렌즈도 개발했다는 기사도 보고 그랬습니다. 그런데, 제대로 돌아가는 회사는 없는 느낌? 원리 https://scent.kisti.re.kr/site/main/archive/article/%EC%83%89%EC%B1%84%EC%9D%98-%ED%96%A5%EC%97%B0%EC%9D%84-%EB%8A%90%EB%81%BC%EA%B2%8C-%ED%95%98%EB%8A%94-%EC%83%89%EB%A7%B9-%EC%95%88%EA%B2%BD%E...
    • 928 질문 그래프 교점이 두개인경우

    • 종강기원

      2025.12.15 - 17:08 5555 2
    • 다음과 같은 식이 있을때 계산기를 돌리면 T가 457인 경우만 구해지는데 T가 410인 경우를 구하는법이 따로 있을까요 교점이 2개 이상일때 모든 값을 구하는 법도 알고 싶습니다
    • 927 일반 미래 AI의 세 번째 임계점: '자율 AI 에이전트'와 '효율성'의 만남
    • 세상의모든계산기 2025.11.06 - 13:04 5566
    • 미래 AI의 세 번째 임계점: '자율 AI 에이전트'와 '효율성'의 만남 첫 번째 임계점이 '계산량'으로 딥러닝의 잠재력을 폭발시켰고, 두 번째 임계점이 '규모'를 통해 LLM의 범용성을 증명했다면, 다가올 세 번째 임계점은 전혀 다른 화두를 던집니다. 바로 '효율성'입니다. 무한정 커질 수 없는 에너지와 비용의 한계 속에서, AI가 한 단계 더 도약하기 위해 반드시 넘어야 할 산입니다. 그리고 이 효율성의 임계점은 우리에게 새로운 차원의 AI, 바로 '자율 AI 에이전트'를 선물할 것입니다. 세 번째 임계점이 만들어낼 AI: 자율 에이전트 ...
    • 926 일반 AI 발전의 두 번째 임계점: LLM과 창발적 능력의 시대. written by gemini-2.5
    • 세상의모든계산기 2025.11.06 - 13:00 5627
    • 첫 번째 임계점에서 GPU와 딥러닝의 만남은 '계산량'이 곧 성능이라는 공식을 증명했습니다. AI는 이미지 인식, 음성 번역 등 특정 작업(Specific Task)에서 인간을 뛰어넘기 시작했습니다. 하지만 AI가 인간처럼 다양한 작업을 수행하는 범용적인 지능을 갖는 것은 여전히 먼 미래의 일처럼 보였습니다. 그리고 2017년 이후, 그 미래를 앞당긴 '두 번째 임계점'이 도래합니다. 바로 대규모 언어 모델(LLM, Large Language Model)의 등장입니다. 기술적 초석: 트랜스포머 아키텍처 LLM 혁명의 시작은 2017년 구글이 발표한 논문 "Attention...
    • 925 일반 AI 발전의 첫 번째 임계점: GPU와 딥러닝 혁명. written by gemini-2.5
    • 세상의모든계산기 2025.11.06 - 12:56 5544
    • AI 발전의 첫 번째 임계점: GPU와 딥러닝 혁명 인공지능(AI) 기술이 지금처럼 세상을 바꾸리라고 모두가 예상했던 것은 아닙니다. 몇 차례의 'AI 겨울'을 겪으며 AI 연구는 더디게만 흘러가던 시기가 있었습니다. 하지만 2012년, AI 역사에 길이 남을 거대한 변곡점이 찾아옵니다. 바로 '딥러닝(Deep Learning)' 알고리즘과 'GPU(Graphics Processing Unit)'라는 하드웨어의 운명적인 만남이었습니다. 이는 AI 발전의 '첫 번째 임계점'으로 기록됩니다. ㄴ 한글은 어려운가? 계산량의 벽에 갇혔던 AI 사실 딥러닝의 핵심 아이디어인 인공 ...
    • 924 일반 ti nspire cx cas2 sgn 함수 입력

    • ㅇㅇ

      2023.12.10 - 06:39 6368 4
    • 안녕하세요. ti nspire cx2 cas 계산기에 sigum 함수를 입력하려면 어떻게 해야하나요? sgn이나 signum이라고 치면 안 나와서 여쭤봅니다.
    • 1 2 3 4 5 6 7 8 9 10 .. 48
    • / 48 GO
    • 글쓰기
    • 세상의 모든 계산기 자유(질문) 게시판
    • 세상의모든계산기
    • 사업자등록번호 703-91-02181
    • 세모계 all rights reserved.