- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
알파고 2.0 ??
-
- 2022.12.02 - 12:36 2017.05.25 - 21:40 1527 13
1. 경향신문 기사 中
작년 3월 이세돌 대국 당시 알파고는 구글이 개발한 AI용 칩인 ‘TPU’ 50개를 동원하는 등 대규모 전산 설비를 썼지만, 올해에는 TPU 4개를 얹은 산업용 컴퓨터(machine) 1대만 썼다.
원문보기:
http://news.khan.co.kr/kh_news/khan_art_view.html?artid=201705251847001&code=970204&nv=stand&utm_source=naver&utm_medium=newsstand&utm_campaign=row1_4#csidx014b2a168e8fece83d99057dbfba69d
2. 블로터 기사 中
이세돌 9단과 대국한 알파고는 구글 클라우드 상 50개의 TPU(Tensor Processing Unit)를 사용했다. TPU는 구글이 머신러닝을 위해 특별히 제작한 처리장치다. 1초에 50개의 수와 10만개의 형태를 탐색할 수 있었다. 현재 커제 9단과 대국 중인 알파고는 ‘알파고 마스터’라고 불리는 버전이다. 이번 구글 I/O 에서 공개된 단일 TPU 머신을 사용하며 2016년 버전 대비 10분의 1의 컴퓨팅 파워를 사용하면서도 더 빨리 계산한다.
http://www.bloter.net/archives/280664
3. NEXTPLATFORM - TPU2에 대한 기사 中
Google’s first generation TPU consumed 40 watts at load while performing 16-bit integer matrix multiplies at a rate of 23 TOPS. Google doubled that operational speed to 45 TFLOPS for TPU2 while increasing the computational complexity by upgrading to 16-bit floating point operations. A rough rule of thumb says that is at least two doublings of power consumption – TPU2 must consume at least 160 watts if it does nothing else other than double the speed and move to FP16. The heat sink size hints at much higher power consumption, somewhere above 200 watts.
https://www.nextplatform.com/2017/05/22/hood-googles-tpu2-machine-learning-clusters/
-
25
댓글13
-
세상의모든계산기
In-Datacenter Performance Analysis of a Tensor Processing Unit ™
https://drive.google.com/file/d/0Bx4hafXDDq2EMzRNcy1vSUxtcEk/view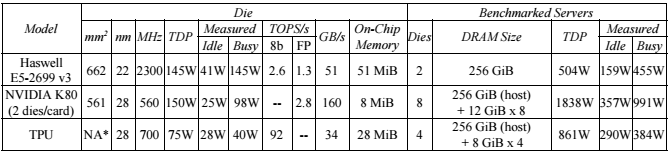
※ 이 논문은 TPU2 가 아닌 TPU(1세대) 을 대상으로 작성된 논문입니다.
-
세상의모든계산기
NVIDIA V100
출처 : https://devblogs.nvidia.com/parallelforall/inside-volta/?ncid=so-fac-vt-13920
Tesla V100 delivers industry-leading floating-point and integer performance. Peak computation rates (based on GPU Boost clock rate) are:
7.5 TFLOP/s of double precision floating-point (FP64) performance;
15 TFLOP/s of single precision (FP32) performance;
120 Tensor TFLOP/s of mixed-precision matrix-multiply-and-accumulate.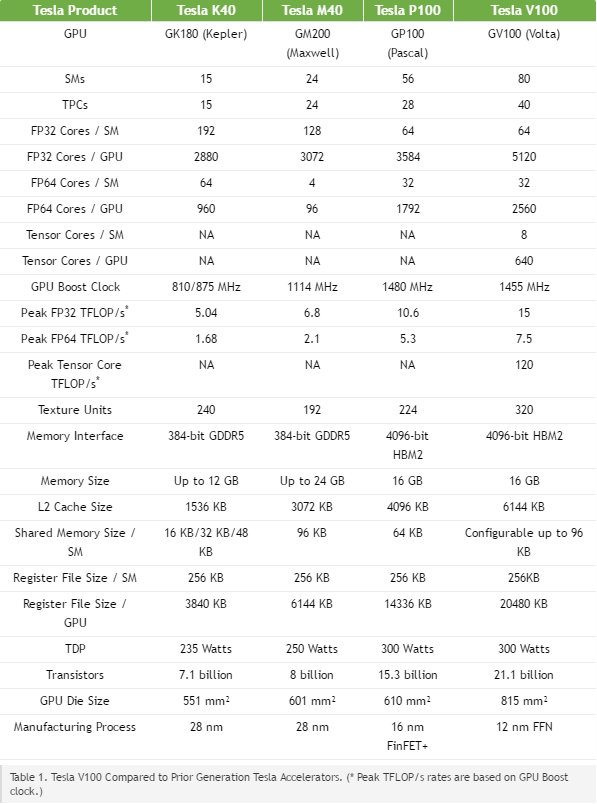
-
세상의모든계산기
팩트 정리를 해 보면...
1. 돌파고의 TPU는 TPU1 으로 불림2. 커파고의 TPU는 TPU2 로 불림
(칩을 TPU2 Chip 으로 부르기도 하는 듯)3. TPU2 모듈 1개는 TPU2코어 4개로 구성
4. TPU2 모듈의 성능 = 45테라플롭스/개*4개 = 180테라플롭스 (
5. https://www.tensorflow.org/tfrc/ 구글 텐서 크라우드?는 100개의 TPU2 모듈로 구성
각각의 TPU2 칩은 두개의 BlueLink 25GB/s 케이블로 연결 -
세상의모든계산기
추정
CPU 종류와 그 비율
출처 : https://www.nextplatform.com/2017/05/22/hood-googles-tpu2-machine-learning-clusters/
We believe that Google connected each CPU board to exactly one TPU2 board using both OPA cables to achieve 25 GB/s aggregate bandwidth. This one-to-one connectivity answers a key question for TPU2 – Google designed the TPU2 stamp with a 2:1 ratio of TPU2 chips to Xeon sockets. That is, four TPU2 chips for every dual-socket Xeon server.> 클라우드가 아닌 싱글머쉰에서 알파고가 돌아갔다면 제온 2소켓 보드 + TPU2 모듈*1개 구성이 맞는 듯
> CPU는 구글 문서에 나온대로 INTEL XEON E5-2699v3 인것 같음. 실질적 계산 역할은 그리 크지 않은 듯.
(seldom 하게 2.3GHz 이외 클럭으로 동작)> 전력소모는 구글 문서에 나온대로 TDP 861W, IDLE 290W, BUSY 384W (싱글머쉰 기준) 이 맞는 듯
세상의모든계산기 님의 최근 댓글
엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10 엑셀 / 행의 최대 개수, 열의 최대 개수, 셀의 최대 개수 엑셀의 행 개수 제한은 파일 형식에 따라 다르며, 최신 .xlsx 파일 형식은 시트당 최대 1,048,576행까지 지원하지만, 구형 .xls 파일은 65,536행으로 제한됩니다. 따라서 대용량 데이터를 다룰 때는 반드시 최신 파일 형식(.)으로 저장해야 하며, 행과 열의 총 수는 1,048,576행 x 16,384열이 최대입니다. 주요 행 개수 제한 사항: 최신 파일 형식 (.xlsx, .xlsm, .xlsb 등): 시트당 1,048,576행 (2^20). 구형 파일 형식 (.xls): 시트당 65,536행 (2^16). 그 외 알아두면 좋은 점: 최대 행 수: 1,048,576행 (100만여개) 최대 열 수: 16,384열 (XFD) 대용량 데이터 처리: 65,536행을 초과하는 데이터를 다루려면 반드시 .xlsx 형식으로 저장하고 사용해야 합니다. 문제 해결: 데이터가 많아 엑셀이 멈추거나 오류가 발생하면, 불필요한 빈 행을 정리하거나 Inquire 추가 기능을 활용하여 파일을 최적화할 수 있습니다. 2026 02.10 [일반계산기] 매출액 / 원가 / 마진율(=이익율)의 계산. https://allcalc.org/20806 2026 02.08 V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04