- TI nspire
두 원이 주어졌을 때, 공통 내접선의 교점과 기울기를 구하는 방법 (프로그램)
문제 : 두 원에 대하여 c1={x1, y1, r1}, c2={x2, y2, r2} 로 입력받았다고 할 때,
공통내접선의 교점과 기울기를 구하려면?
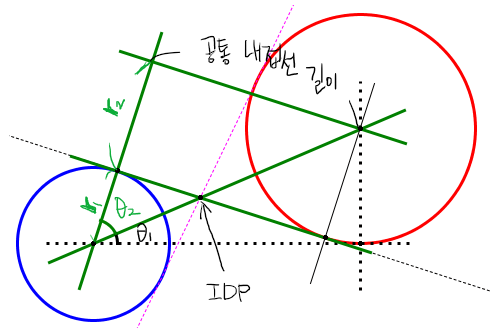
- 내접선의 교점은 두 원의 중심을 이은 직선을 r1:r2 로 내분한 점(idp)과 같다.
ㄴ Internally Dividing Point
- 1.의 내분점(IDP) 과 c1 사이의 거리, IDP와 접선의 (c1에서의) 접점 사이의 거리를 구한다.
ㄴ IDP와 접선의 접점 사이 거리 = 내접선의 길이 * 내분 비율
- 각도 t1, t2를 구한다.
t1 = c1과 c2의 중점을 잇는 직선이 x축과 이루는 각
t2 = c1에서의 공통내접점 ~ 원의 중심 ~ IDP 사잇각
- 4. t1, t2를 이용해 기울기를 구한다.
아래는 TI-nspire 에서 작성된 프로그램입니다.
Define common_itl()=
Prgm
:© Request basic data for 2 circles
:Request "{x1,y1,r1} List =",circle1,0
:Request "{x2,y2,r2} List =",circle2,0
:
:© Check data compatibility
:If (circle2[1]-circle1[1])^(2)+(circle2[2]-circle1[2])^(2)<(circle1[3]+circle2[3])^(2) Then
: Disp "Too close"
: Goto end
:EndIf
:
:newList(3)→circle3
:
:© Redefine vars to draw graph
:circle1[1]→circle1.x
:circle1[2]→circle1.y
:circle1[3]→circle1.r
:circle2[1]→circle2.x
:circle2[2]→circle2.y
:circle2[3]→circle2.r
:
:© Calculate Internally Dividing Point
:((circle1[3]*circle2[1]+circle2[3]*circle1[1])/(circle1[3]+circle2[3]))→idp.x
:((circle1[3]*circle2[2]+circle2[3]*circle1[2])/(circle1[3]+circle2[3]))→idp.y
:
:© Calculate Distances between IDP and the center of circles
:Local circle1.ratio,circle2.ratio
:((circle1[3])/(circle1[3]+circle2[3]))→circle1.ratio
:((circle2[3])/(circle1[3]+circle2[3]))→circle2.ratio
:
:√((circle2[1]-circle1[1])^(2)+(circle2[2]-circle1[2])^(2))→distance.c1c2
:distance.c1c2*circle1.ratio→distance.c1idp
:distance.c1c2*circle2.ratio→distance.c2idp
:
:√(distance.c1c2^(2)-(circle1[3]+circle2[3])^(2))→distance.citl
:distance.citl*circle1.ratio→circle3.r
:circle3.r→circle3[3]
:
:© Calculate Slope of Tangent Line
:tan(((circle2[2]-circle1[2])/(circle2[1]-circle1[1])))→t1
:tan(((circle3[3])/(circle1[3])))→t2
:
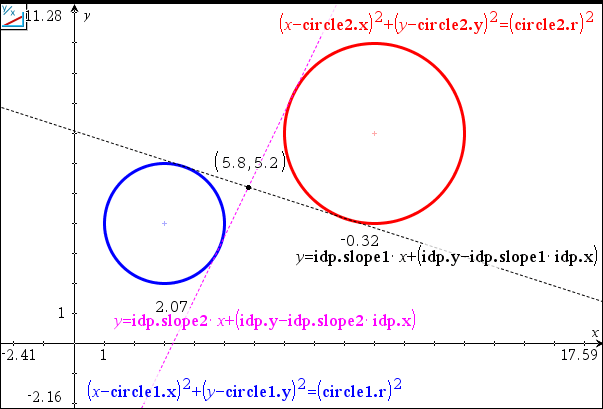
:tan(t1+t2+((π)/(2)))→idp.slope1
:tan(t1-t2+((π)/(2)))→idp.slope2
:
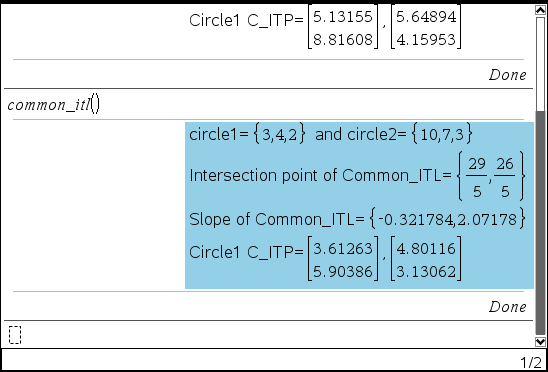
:Disp "circle1=",circle1," and circle2=",circle2
:Disp "Intersection point of Common_ITL=",{idp.x,idp.y}
:Disp "Slope of Common_ITL=",approx({idp.slope1,idp.slope2})
:c1_itp()
:
:Lbl end
:EndPrgm
댓글1
-
세상의모든계산기
C1에서의 공통 내접선의 접점을 구하려면?
- C1과 C3을 연립하여 풀거나,
ㄴ C3는 (idp,x,idp.y)를 중심으로 하고 위에서 구한 circle3.r 을 반지름으로 하는 원 - c1->idp 벡터를 (t2)만큼 회전하고 scalar 곱하여 구할 수 있음.
[[cos(θ),−sin(θ)][sin(θ),cos(θ)]]→rot_matrix(θ)
((circle1.r)/(distance.c1idp))*rot_matrix(±t2)*(vector.c3-vector.c1)+vector.c1
- C1과 C3을 연립하여 풀거나,


세상의모든계산기 님의 최근 댓글
은행앱 통합하면서 없어졌나보네요. ㄴ 비슷한 기능 찾으시는 분은 : 스마트 금융 계산기 검색해 보세요. https://play.google.com/store/apps/details?id=com.moneta.android.monetacalculator 2026 01.25 Ctrl+Z 를 이용해 뒤로 돌아기기 Undo 기능이 있는지 살펴보세요. 2026 01.23 쌀집계산기로 연립방정식 계산하기 - 크래머/크레이머/크라메르 공식 적용 https://allcalc.org/56739 3. 'x' 값 구하기 계산기 조작법 목표: x = Dx / D = [(c×e) - (b×f)] / [(a×e) - (b×d)] 계산하기 1단계: 분모 D 계산 (메모리 활용) 1 * 1 M+ : 메모리(M)에 1를 더합니다. (현재 M = 1) -0.1 * -0.2 M- : 메모리(M)에서 0.02를 뺍니다. (현재 M = 0.98 = 0.98) 이로써 메모리(MR)에는 분모 0.98가 저장됩니다. 2단계: 분자 Dx 계산 후 나누기 78000 * 1 : 78000를 계산합니다. = : GT에 더합니다. -0.1 * 200000 : -20000를 계산합니다. ± = : 부호를 뒤집어 GT에 넣습니다. // sign changer 버튼 사용 GT : GT를 불러옵니다. GT는 98000 (분자 Dx) 값입니다. ÷ MR = : 위 결과(98000)를 메모리(MR)에 저장된 분모 D(0.98)로 나누어 최종 x값 100,000를 구합니다. 4. 'y' 값 구하기 계산기 조작법 목표: y = Dy / D = [(a×f) - (c×d)] / [(a×e) - (b×d)] 계산하기 1단계: 분모 D 계산 (메모리 활용) 'x'에서와 분모는 동일하고 메모리(MR)에 0.98가 저장되어 있으므로 패스합니다. 2단계: 분자 Dy 계산 후 나누기 GT ± = : GT를 불러오고 부호를 뒤집어 GT에 더합니다. GT가 0으로 리셋됩니다. 【AC】를 누르면 M은 유지되고 GT만 리셋되는 계산기도 있으니 확인해 보세요. 1 * 200000 : 200000를 계산합니다. = : GT에 더합니다. 78000 * -0.2 : -15600를 계산합니다. ± = : 부호를 뒤집어 GT에 넣습니다. GT : GT를 불러옵니다. 215600 (분자 Dy) 값입니다. ÷ MR = : 위 결과(215600)를 메모리(MR)에 저장된 분모 D(0.98)로 나누어 최종 y값 220,000를 구합니다. x, y 값을 이용해 최종 결과를 구합니다. 2026 01.18 크레이머 = 크레머 = 크라메르 공식 = Cramer's Rule https://allcalc.org/8985 2026 01.18 부호 변경, Sign Changer 버튼 https://allcalc.org/52092 2026 01.18