- TI nspire
함수 Completesquare, 완전제곱식 변환 기능
① completeSquare(수식 또는 방정식, 변수) ⇒ 수식 또는 방정식
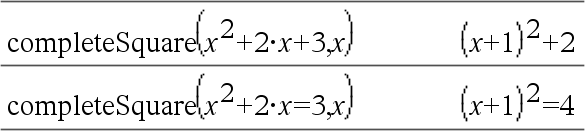
② completeSquare(수식 또는 방정식, 변수^거듭제곱) ⇒ 수식 또는 방정식
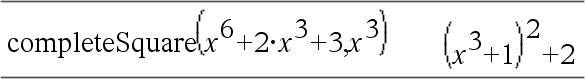
③ completeSquare(수식 또는 방정식, 변수1, 변수2 [,...]) ⇒ 수식 또는 방정식
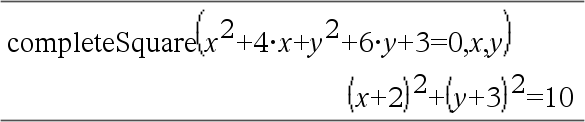
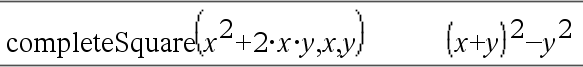
④ completeSquare(수식 또는 방정식, {변수1, 변수2 [,...]}) ⇒ 수식 또는 방정식
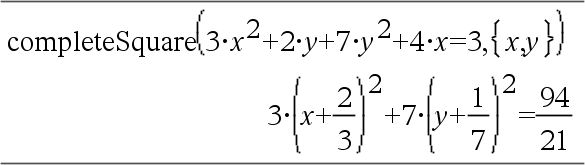
a•x²+b•x+c 형태의 2차 다항식을 a•(x-h)²+k 형태로 변환합니다.
- 또는 -
a•x²+b•x+c = d 형태의 2차 방정식을 a•(x-h)² = k 형태로 변환합니다.
첫 번째 인수는 두 번째 인수에 대한 표준 형식의 2차 수식 또는 방정식이어야 합니다.
두 번째 인수는 단일 단변량 항이거나 유리수 거듭제곱으로 올려진 단일 단변량 항이어야 합니다(예: x, y², 또는 z^(1/3)).
세 번째③와 네 번째④ 구문은 변수 Var1, Var2 [,… ]에 대해 완전제곱식을 시도합니다.


세상의모든계산기 님의 최근 댓글
그래프로 확인 매우 작은 구간으로 그래프를 확대해 보면 불연속적인 모습이 확인됩니다. 이것은 한계 digits(15자리) 이상을 처리하지 못하기 때문입니다. 2025 10.21 tns 파일 첨부 sol_num_vs_exact.tns 2025 10.21 검증하면 1번 식을 x에 대해 정리하고, → 그 x 값을 2번 식에 대입해 넣으면 → 그 결과로 x는 사라지고 y에 대한 식이 되니, y에 대해 정리하면 참값 y를 얻음. 얻은 y의 참값을 처음 x에 대해 정리한 1번식에 대입하면 참 값 x를 얻음. 구해진 참값의 근사값을 구하면 x=73.049507058547 and y=23.747548955927 어떤 solve로 나온 근사값이든, 근사값으로는 원래의 식 모두를 만족시킬 수 없음. 2025 10.21 그렇다면 해의 참 값은? 먼저, 모든 decimal 값을 유리수로 변환하고, solve 로 답을 구함. 변수 x로는 구해지는데 y로는 "Error: Resource exhaustion" 발생 // 이유는 모름. approx(exsol1) x=73.049507058547 and y=23.747548955927 2025 10.21 각 결과값의 비교 x y {x} 73.049507058553 23.747548955926 {y} 73.049507058479 23.747548955927 {x=1,y=1} 73.049507058477 23.747548955927 approx() 전처리 73.049507058479 23.747548955926 linsolve 73.049507058478 23.747548955926 approx(참 해) 73.049507058547 23.747548955927 * 구해진 x값들은 차이가 비교적 큰데, y값들은 차이가 적은 편입니다. 2025 10.21