- TI nspire
[TI-Nspire] 기본 기능을 이용한 라플라스 변환
한국어로 번역한 문서 https://allcalc.org/50260 를 TI-Nspire 용으로 추가 가공한 문서입니다.

소개
TI 계산기에는 라플라스 변환과 역변환을 계산하기 위한 미리 프로그래밍된 함수가 없습니다.
하지만 여러 웹사이트에서 이를 제공합니다 :
역자 주) TI-nspire 용으로 컨버팅 해당 문서는 https://allcalc.org/5003 입니다.
여기서 우리가 제안하는 것은, "TI의 기본 함수만을 사용하여도 충분히 잘 해낼 수 있다는 것을 보여주는 것"입니다.
라플라스 변환
먼저 라플라스 변환은 매개변수 s의 특정 값에 대해 수렴하는 이상적분임을 주목해야 합니다:
$ f\left( t\right) \leftrightarrow F\left( s\right) \equiv \int _{0}^{\infty }f\left( t\right) \cdot e^{-s\cdot t}dt $
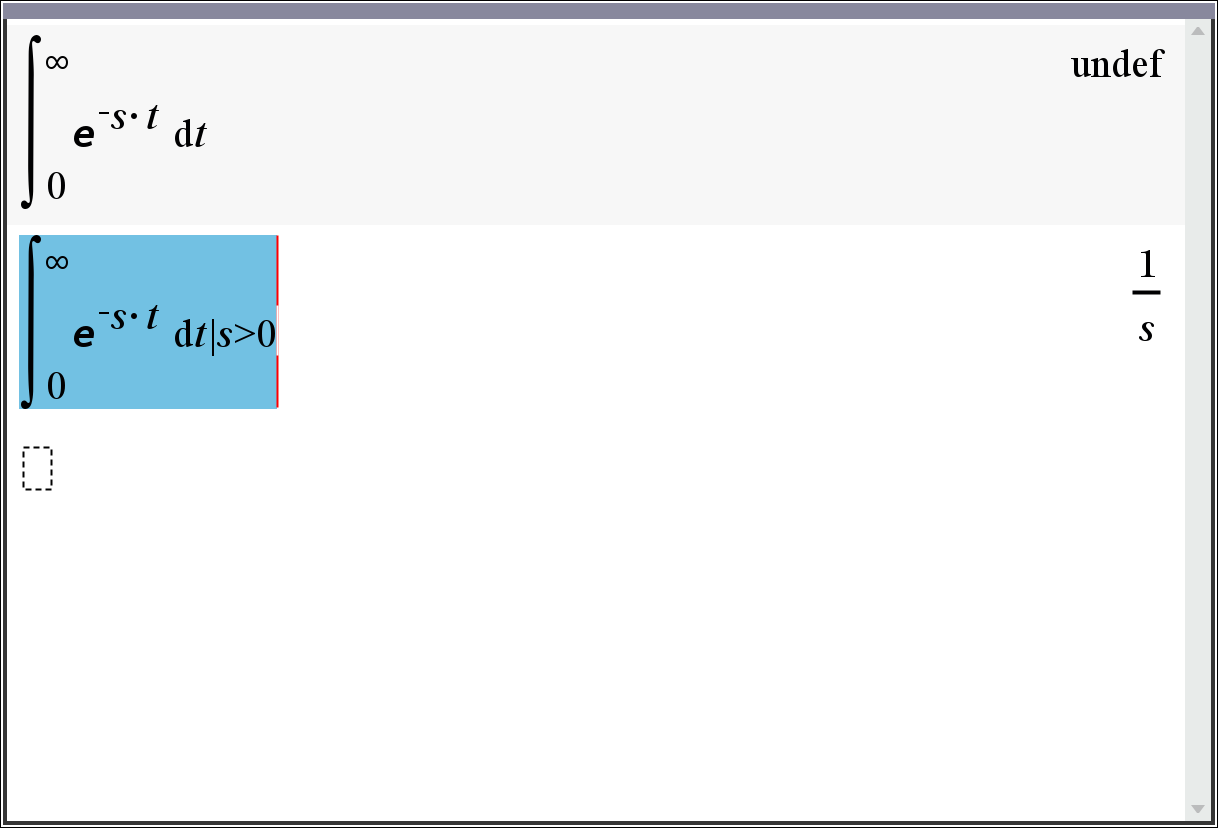
TI는 s에 대한 도메인이 지정되지 않으면 정의할 수 없습니다. (그림 1).∫(e^(−s*t),t,0,∞)|s>0
라플라스 변환을 함수로 정의할 수 있습니다.

하지만 TI-89와 달리 제약연산자(|) 를 한꺼번에 넣어서 정의하면 조각함수(piecewise function) 로 바뀌면서 오류가 발생합니다.
따라서 TI-nspire에서는 제약연산자 부분을 함수정의와 분리하고, 다시 함수와 결합해 사용해야 하는 불편함이 있습니다.
TI-89 에서는 위의 la(f,t,s) 함수의 수렴이 느려서 Lim 함수를 결합한 lala(f,t,s) 함수라는 대안을 찾았지만,
TI-nspire 에서는 속도가 충분히 빨라졌기 때문에 속도 때문에 대안을 찾을 필요는 없고,
다만 TI-89 에서 찾은 대안을 Nspire에서 사용하면 제약 연산자를 재결합해서 사용하지 않아도 되기 때문에
TI-nspire 에서도 유용한 대안이 됩니다.
* 여기서는 lala(f,t,s) 대신 lapl(f,t,s) 라는 함수명을 사용하겠습니다.

ㄴ lapl(f,t,s) := −lim(∫(f*e^(−s*t),t),t,0,1)
무한대에서의 값이 0이 됨을 이용하여 부적절한 적분(undef)을 피할 수 있습니다.
실제로, 라플라스 변환을 계산하는 함수들은 지수 차수입니다. 이는 s를 충분히 크게 선택하면
$ \lim _{t\rightarrow \infty }f\left( t\right) \cdot e^{-s\cdot t}=0 $ 을 얻게 된다는 것을 의미합니다.
부정적분 을 계산한 후에는 (f가 모든 곳에서 연속이고 TI가 적분 상수를 추가하지 않는다고 가정하면)
$ \int f\left( t\right) \cdot e^{-st}dt $ 라고 하면 됩니다.
극한은 t = 0에서의 평가가 0의 오른쪽에서 계산되어야 한다는 사실에서 비롯됩니다.
이제 훨씬 더 심각한 문제인 역변환을 다루겠습니다.
역 라플라스 변환
$ F\left( s\right) =\dfrac{1}{\left( s-2\right) ^{2}\cdot \left( s^{2}+6s+13\right) } $
의 역변환 계산을 고려해 봅시다.
여기서는 제곱 완성을 수행해야 합니다: 부분 분수 전개 전에 이를 수행하는 것이 좋습니다(그림 3).

변환 표에서 다음과 같은 대응관계를 알아야 합니다:
$ \dfrac{s+a}{\left( s+a\right) ^{2}+b^{2}}\leftrightarrow e^{-at}\cos bt,\dfrac{b}{\left( s+a\right) ^{2}+b^{2}}\leftrightarrow e^{-at}\sin bt $
$ \dfrac{1}{s+a}\leftrightarrow e^{-at}\text{ and }\dfrac{1}{\left( s+a\right) ^{2}}\leftrightarrow t\cdot e^{-at} $
따라서 답은
$ f\left( t\right) =\dfrac{10e^{-3t}\cos 2t}{841}+\dfrac{21e^{-3t}\sin 2t}{1682}-\dfrac{10e^{2t}}{841} +\dfrac{t \cdot e^{2t}}{29} $
입니다.
컨볼루션으로도 진행할 수 있습니다:
컨볼루션 속성에 따르면 F(s) = X(s) H(s)인 경우,
$ \text{with } F\left( s\right) \leftrightarrow f\left( t\right), X\left( s\right) \leftrightarrow x\left( t\right) \text{ and } H\left( s\right) \leftrightarrow h\left( t\right), $
$ \text{then } f\left( t\right) = x\left( t\right) \ast h\left( t\right) \equiv \int _{0}^{t}x\left( \tau \right) h\left( t-\tau \right) d\tau $
입니다.
여기서 우리는 다음 식을 얻습니다. :
$ F\left( s\right) =\dfrac{1}{\left( s-2\right) ^{2}\cdot \left( s^{2}+6s+13\right) } $
$ =\left( \dfrac{1}{\left( s-2\right) ^{2}}\right) \left( \dfrac{1}{\left( s+3\right) ^{2}+4}\right) \leftrightarrow t\cdot e^{2t}\ast \dfrac{1}{2}e^{-3t}\sin 2t $
그리고 TI는 컨볼루션 적분을 처리합니다(그림 4 a 참조).
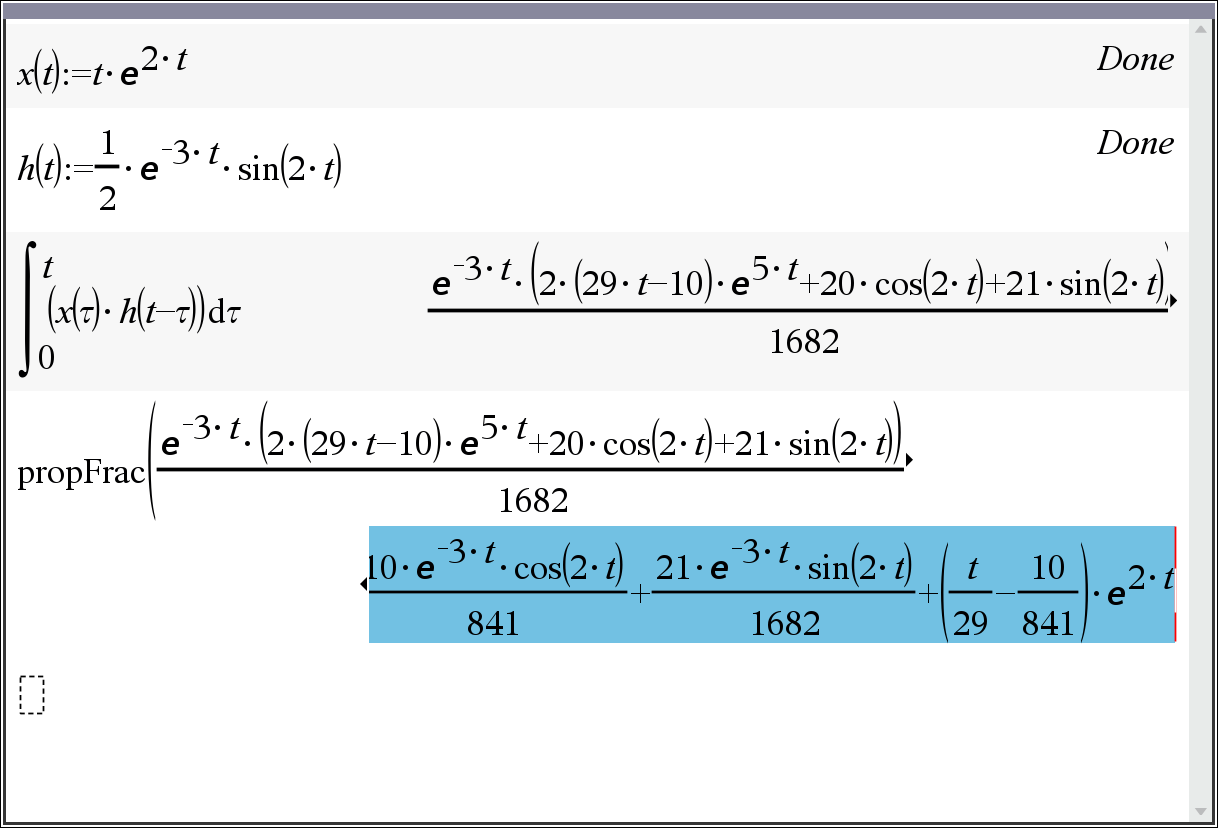
그림 4 b와 4 c는 결과의 단순화를 보여줍니다.
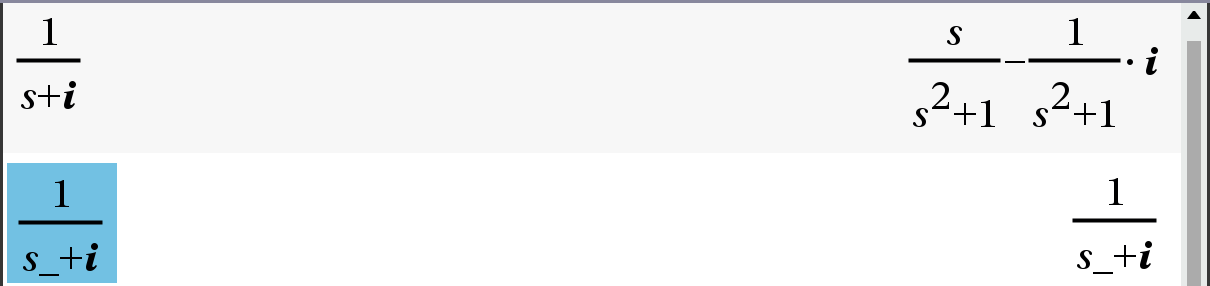
복소수를 사용하여 부분 분수로 전개할 수도 있습니다.
TI에서 선언되지 않은 변수는 실수로 간주되지만, 이 변수에 밑줄 "_" 기호를 추가하면 복소수로 간주됩니다.
실제로 s가 실수인지 복소수인지에 따라 TI가 $ \dfrac{1}{s+i} $ 를 어떻게 단순화하는지 보세요(그림 5).
이 단계에서 대응관계 $ \dfrac{1}{s+a} \leftrightarrow e^{at} [ Re\left( s\right) > -a] $ 와
오일러 공식 $e^{it} =\cos(t) + i \sin(t) , \left( t\in R\right) $ 을 사용하면 복소 부분 분수가 수행된 후 역 라플라스 변환을 계산할 수 있습니다.
여기서 g(s)라고 부를 $ F\left( s\right) =\dfrac{1}{\left( s-2\right) ^{2}\cdot \left( s^{2}+6s+13\right) } $ 의 예를 다시 살펴봅시다.
부분 분수로 전개하기 전에 복소수로 인수분해하는 것이 중요합니다(그림 6 a);

이 작업은 s가 복소수라는 제약 하에 수행됩니다(그림 6 b 및 6 c).
그런 다음 복소 근이 켤레 쌍으로 나타난다는 사실을 이용하여
$ ze^{\left( 3+2i\right) t}+\overline{z}e^{\left( 3-2i\right) t}-\dfrac{10}{841}e^{2t}+\dfrac{1}{29}te^{2t}$ 라고 쓰면 됩니다.
여기서 z는 숫자 $ z = \dfrac{5}{841} + \dfrac{21}{3364}i $ 로 정의되었습니다.
TI는 "conj"를 사용하여 복소수를 켤레복소수로 만듭니다(그림 7).

미분방정식 시스템과 라플라스 변환
TI는 라플라스 변환을 사용하여 미분방정식 시스템을 해결하는 데 매우 유용할 수 있습니다.
계산기가 길고 지루한 계산을 처리하므로 사용자는 해결할 방정식만 지정하면 됩니다.
다음 시스템을 고려해 봅시다:
$ \begin{cases}\dfrac{dx}{dt}-3x-6y=27t^{2},,x\left( 0\right) =5\\ \dfrac{dx}{dt}+\dfrac{dy}{dt}-3y=5e^{t},y\left( 0\right) =-1\end{cases} $
s 도메인으로 변환하면 다음을 얻습니다:
$ \begin{cases}sX-5-3X-6Y=\dfrac{54}{s^{3}}\\ sX-5+sY+1-3Y=\dfrac{5}{s-1}\end{cases} $
여기서 X와 Y는 각각 x와 y의 라플라스 변환을 나타냅니다. 마지막으로, 우리 시스템을 행렬 형태로 다시 쓰면 다음을 해결해야 합니다:
$ \begin{bmatrix} s-3 & -6 \\ s & s-3 \end{bmatrix}\begin{bmatrix} X \\ Y \end{bmatrix}=\begin{bmatrix} \dfrac{54}{s^{3}}+5 \\ \dfrac{5}{s-1}+4 \end{bmatrix} $
TI가 개입하고 우리는 행렬을 정의합니다(그림 8).

계수 행렬을 m이라고 부르고 오른쪽 행렬을 b라고 부르기로 합니다.
좋은 옛날 크라머 방법은 이제 쓸모없어졌습니다!
실제로 TI의 "simult" 함수를 사용하면 정사각형 선형 시스템을 해결할 수 있습니다(그림 9).
지루한 행렬식의 몫을 계산할 필요가 없습니다(또는 를 입력해도 결과는 같았을 것입니다).
이제 부분 분수로 전개하기만 하면 됩니다.
"expand" 명령은 리스트와 행렬에서도 작동합니다. "expand"의 구문은 expand(exp [, var])입니다. (그림 10).
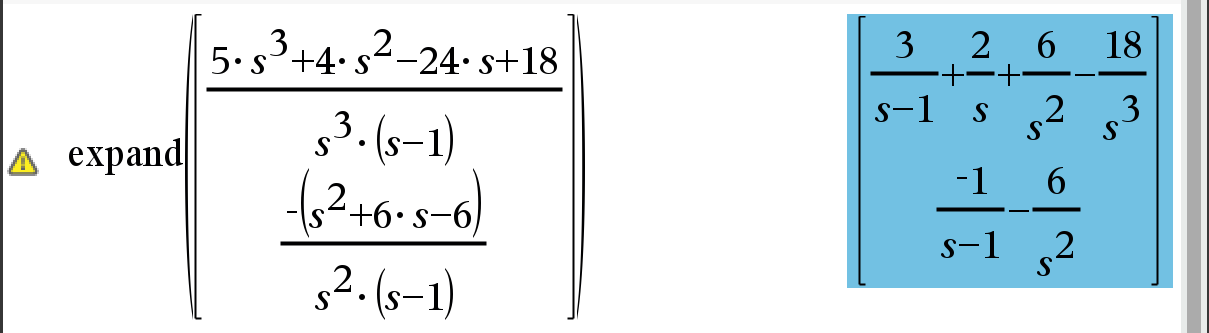
라플라스 변환 표를 사용하여 다음과 같이 쓸 수 있습니다:
$ x\left( t\right) =3e^{t}+2+6t-9t^{2} $
$ y\left( t\right) =-e^{t}-6t $


세상의모든계산기 님의 최근 댓글
예시11) 선형 연립방정식에서 답이 false 로 나올 때 https://allcalc.org/55823 2025 10.22 approx(참 해) 값이 이상하게 튀는 것 같아서 AI를 이용해 (python 으로) 구해보았습니다. * python 의 유효자릿수가 nspire 의 유효자릿수(14자리~15자리)보다 더 길기 때문에 시도하였습니다. ** 원래는 wolfram alpha 로 구해보려고 했는데, 울프람에서는 수식 길이가 너무 길다고 거부하는 바람에 포기하였습니다. 그 결과, AI approx(참 해) 값은 정상 범주에 포함되었고, 이는 solve()로 구한 대부분의 결과값과 유사하였습니다. 그럼 nspire 의 approx(참 해)는 왜 튀었나? 참 해에 더하기,빼기,곱하기,나누기 가 너무 많이 포함되어 있다보니, 모두 계산하고 나면 오차가 누적&증폭되어 버리는 것 같습니다. 그래서 오히려 solve의 numeric 한 접근보다도 더 큰 오차가 발생한 듯 하고, 그래서 적절한 해의 x 구간을 벗어나버린 듯 합니다. 그것이 처음의 solve 에서 false 를 이끌어낸 주 원인이 아니었을까요? (추정) 2025 10.21 그래프로 확인 그래프 함수로 지정하고, 매우 좁은 구간으로 그래프를 확대해 보면 불연속적인 그래프 모습이 확인됩니다. 이것은 한계 digits(15자리) 이상을 처리하지 못하기 때문일 것이구요. 다만 특이한 점은, 그래프상으로 교점에 해당하는 구간이 73.049507058477≤x≤73.049507058484 사이로 나오는데 -> 이 구간은 'solve에서 여러 방법으로 직접 구해진 해들'은 포함되는 구간입니다. -> 하지만, '참값인 해를 계산기로 구한 appprox 값 x=73.049507058547'은 포함되지 않는 구간입니다. 2025 10.21 tns 파일 첨부 sol_num_vs_exact.tns 2025 10.21 검증하면 1번 식을 x에 대해 정리하고, → 그 x 값을 2번 식에 대입해 넣으면 → 그 결과로 x는 사라지고 y에 대한 식이 되니, y에 대해 정리하면 참값 y를 얻음. 얻은 y의 참값을 처음 x에 대해 정리한 1번식에 대입하면 참 값 x를 얻음. 구해진 참값의 근사값을 구하면 x=73.049507058547 and y=23.747548955927 참 값을 approx() 로 변환한 근사값은 원래 방정식 모두를 만족할 수 없지만, linsolve() 로 찾은 근사값과, AI로 참 값을 근사변환한 값은 원래 방정식 모두를 만족할 수 있습니다. 2025 10.21