[fx-570][fx-350] (2차) 회귀 분석으로 2변수 (2-Var) 통계 분석 하기

SINCE 2015.01.19.
세모계
SEARCH

세모계
by ORANGEDAY

CASIO

CASIO 공통

[fx-570][fx-350] (2차) 회귀 분석으로 2변수 (2-Var) 통계 분석 하기

- 세상의모든계산기
- 2024.09.26 - 00:37 2016.04.20 - 13:44 8854 4

1. 2변수 분석? 2-Var Statistics

[fx-350] 이나 [fx-570] 시리즈의 통계모드에는 1-Var (1-변수) 분석 기능이 있습니다. 즉 x 라는 변수 리스트에 있는 DATA 의 평균, 합(∑x), 표준편차(sx, σx) 등을 구하는 기능입니다.

여기서 한발 나아가서 두가지 변수를 한꺼번에 분석하면 좋은데 이들 계산기에는 '2-Var 모드'가 따로 마련되어 있지 않습니다.
하지만, 포기하긴 이르죠.

2. 회귀 분석(Regression)의 활용

회귀(Regression) 분석은 'x변수 DATA와 y변수 DATA 의 관계(식)를 찾아내는 것'입니다.

그래서 필수적으로 x와 y 를 각각 그리고 같이 분석하는 과정을 거쳐야 합니다.

그렇습니다. '2-Var 통계 분석'은 회귀분석 과정에 포함되어 있으니, 여기에서 필요한 결과 값만 뽑아 쓰면 되는 겁니다.

회귀 분석 모드는 여러 방정식 형태로 찾을 수 있는데, 회귀 결과를 찾는 과정이 아니라면, 선형이든 뭐든 아무꺼나 사용하셔도 관계가 없습니다.

3. 2-Var 통계분석 예제 [fx-570ES]

※ 변수 DATA

x	y
166	55
174	70
171	70
180	83

└ y 에는 x의 확률값을 넣을 수 없습니다.

통계 모드 선택 (2차 회귀)
【MODE】【3】【3】

* 선형 회귀(A+BX)를 선택해도 상관은 없습니다만, 여기서는 2차 회귀를 선택하였습니다.
DATA 입력

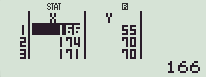
다 입력하고 【AC】

통계변수값 확인

【SHIFT】【1】【3】 Sum	∑(x^2) ∑x ∑(y^2) ∑y ∑(xy) ∑(x^3) ∑(x^2y) ∑(x^4)
【SHIFT】【1】【4】 Var	변량 : n 평균 : x바, y바 모 표준편차 : σx, σy 표본 표준편차 : sx, sy
【SHIFT】【1】【5】 Reg	회귀 분석 결과이므로 안봐도 됨

여기에 나오지 않는 통계값은 위 통계값들을 활용해서 구합니다.

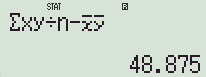
예) x-y 공분산

Attached file

이 게시물을..

25

세상의모든계산기
계산기는 거들 뿐
혹은
계산기를 거들 뿐

글쓴이의 서명작성글 감추기

0

품질
2016.05.18 - 15:10 #18167

N위치가 마지막으로 가야 맞네요^^

댓글 수정 삭제
1

0

세상의모든계산기
2016.05.21 - 16:57 2016.05.18 - 17:26 #18181

마지막 공분산을 말씀하시는 것인가요?
통계를 잘 모릅니다만, 공식에 따르면 n 위치는 맞습니다.

공분산 = 48.875
σx ≒ 5.068
σy ≒ 9.912

상관계수(r) ≒ 0.973 ≒ 48.875/(5.068*9.912)

댓글
0

공분산 어케구하나요?
2016.06.10 - 22:02 #18356

카시오 fx-570es plus 쓰고있는데요 공분산 어떻게 구하는건가요???
위의 시그마xy 나누기 갯수 빼기 x평균y평균해도 참값이 안나오던데요 ㅜㅠ

댓글 수정 삭제
1

0

세상의모든계산기
2016.06.11 - 09:29 #18366

표본 공분산인 경우에는 n 대신 n-1 을 사용합니다.
그게 아니면 안나올 이유가 없고, 질문을 이렇게 하시면 답변을 할 수가 없습니다.

[필독] 계산기 질문글 작성시 주의사항! (부제 : 바람직한 질문글 작성 요령)
http://www.allcalc.org/5227

댓글

댓글 쓰기 에디터 사용하기 닫기

view_headline 목록

14px

[fx-9860] 행렬에 복소수를 넣어 계산할 수 있나? (=연립방정식 복소수계수/복소수근 구하기)
[fx-570MS] 공학용 단위 표기 설정 Mode - Disp - Eng on/off
목록
view_headline

× CLOSE - KEEP CLOSED

전체 9860 41 570 49 350 2 기타 11 공통 26

분류 정렬 검색

72 9860 [fx-9860] 행렬에 복소수를 넣어 계산할 수 있나? (=연립방정식 복소수계수/복소수근 구하기)
세상의모든계산기 2015.12.03 - 19:09 9652 4
1. [fx-9860G] 모델(II 포함)에서 행렬의 원소에 복소수를 넣을 수 있나? OS Ver 1.xx 에서는 안됩니다. 행렬 안에 복소수를 강제로 집어 넣으면, 위 스샷처럼 Ma ERROR 메시지를 내뿜습니다. 그렇다면 행렬에서는 복소수를 이용할 방법이 전혀 없을까요? OS Ver 2.0 이상이라면 가능합니다. 간단하죠. ^^ 2. 복소수 연립 방정식의 해 - MATRIX & RREF 복소수 계수를 입력할 수만 있다면, 실수 계수인 연립방정식의 해를 찾는 것과 과정은 같습니다. 연립방정식의 풀이법 (System of linear equations) 생성 가능한 행렬 크기에 제약만 없...

공통 [fx-570][fx-350] (2차) 회귀 분석으로 2변수 (2-Var) 통계 분석 하기
세상의모든계산기 2016.04.20 - 13:44 8854 4
1. 2변수 분석? 2-Var Statistics [fx-350] 이나 [fx-570] 시리즈의 통계모드에는 1-Var (1-변수) 분석 기능이 있습니다. 즉 x 라는 변수 리스트에 있는 DATA 의 평균, 합(∑x), 표준편차(sx, σx) 등을 구하는 기능입니다. 여기서 한발 나아가서 두가지 변수를 한꺼번에 분석하면 좋은데 이들 계산기에는 '2-Var 모드'가 따로 마련되어 있지 않습니다. 하지만, 포기하긴 이르죠. 2. 회귀 분석(Regression)의 활용 회귀(Regression) 분석은 'x변수 DATA와 y변수 DATA 의 관계(식)를 찾아내는 것'입니다. 그래서 필수적으로 x와 y 를 각각 그...

70 570 [fx-570MS] 공학용 단위 표기 설정 Mode - Disp - Eng on/off
세상의모든계산기 2015.11.18 - 22:56 4454 2
1. 공학용 단위 Eng 표기란? 공학에서는 10(3배수) 단위로 숫자를 구분하는 것을 좋아합니다. 10(15)=P, 10(12)=T, 10(9)=G, 10(6)=M, 10(3)=K 10(-15)=f, 10(-12)=p, 10(-9)=n, 10(-6)=μ, 10(-3)=m "SI 접두어, SI Prefixes, Metric Prefixes"라고도 부르는 그것인데요. 일부 공학용 계산기에는 공학용 단위를 기준으로 결과값을 표기하도록 설정할 수 있습니다. 이 SI 접두어 알파벳 단위로 숫자가 표시됩니다. [fx-570 MS]가 바로 그런 계산기의 하나입니다. MS 기종에서 가능하다가, ES 기종에서 기능이 없어졌고, EX 기종에서는 다시 ...

69 570 [fx-570ES] STAT 통계 - 편차제곱의 합. SSX 또는 SSY
세상의모든계산기 2024.09.18 - 20:37 752 1
편차제곱의 합은 통계학에서 데이터의 분산과 표준편차를 계산할 때 중요한 개념입니다. 이를 이해하기 위해 먼저 편차를 정의해야 합니다. 1. 편차 (Deviation): 편차는 각 데이터 값이 평균에서 얼마나 떨어져 있는지를 나타내는 값입니다. 수식으로는 다음과 같습니다. \[ \text{편차} = x_i - \mu \] 여기서: - $ x_i $는 각 데이터 값 - $ \mu $는 데이터 값들의 평균입니다. 2. 편차제곱 (Squared Deviation): 편차는 양수 또는 음수일 수 있기 때문에, 이 값들을 제곱하여 편차제곱을 구합니다. 이는 음수와 양수를 구분하지 않...

68 카시오 글꼴 Font Sets
세상의모든계산기 2015.01.26 - 14:02 1011 4
Font Sets 다운로드 사이트 http://edu.casio.com/education/fontset/ 2024-06-26 현재 아래 모델들의 폰트가 있습니다. -> 다운로드 클릭해도 다운되지 않으면 위 링크에 직접 가셔서 agreement 체크하시고 다운받으시면 됩니다. CAS Graphic Models fx-CP400 (Class Pad II) Download CAS Graphic Models ClassPad 330 PLUS ClassPad 300/330 Download Graphic Models fx-CG series fx-9860GII/fx-9860G series Download ClassWiz CW Models ClassWiz CW series Download ClassWiz EX Models ClassWiz EX series Download Natural Textbo...

67 570 [fx-570ES] 로그의 입력 log
세상의모든계산기 2024.09.12 - 17:11 693
1. fx-570 ES 및 EX 로그 템플릿 버튼이 있어서 쉽게 로그값을 입력할 수 있습니다. 2. 한줄입력 LINE IO 설정시 로그 입력 fx-570ES 는 밑을 입력하여 변경할 수 있는 계산기이지만, 한줄 입력 설정이 되면 커서가 밑의 위치로 이동할 수 없기 때문에 한줄로 밑과, 진수를 입력해야 합니다. 이 때, log(밑, 진수) 순서로 입력하며 컴마는 【SHIFT】【)】 로 입력합니다. * 위에 보시는 것처럼 특정 모드에서는 Math IO 에서 강제로 LINE IO 로 변경됩니다. - STAT(통계), MAT(행렬), VCT(벡터) 모드에서 Math IO 로 설정할 수 없습니다.

66 570 [fx-570] [ES/MS] 내장 과학상수 번호 CONST #
세상의모든계산기 2016.01.12 - 12:57 7890 7
1. 과학 상수란? 과학 상수(Scientific Constants)란, 물리학/화학/생물학 등 과학에서 자주 사용되는 상수값을 부르는 말입니다. 공학용 계산기 중에는 과학 상수 중 일부를 상수로서 내장하고 있는 것이 있습니다. 내장된 상수명을 계산식에 사용하면 식을 간소화할 수 있어서 보기에도, 입력하기에도 편합니다. 덤으로 잘 못 입력하는 실수를 줄일 수도 있겠죠. 아래는 카시오 [fx-570] 기종(ES, MS)의 내장 과학상수 목록표입니다. (총 40개) [fx-350] 시리즈에는 과학상수가 없습니다. 그런데 과학 상수의 대부분은 절대의 진리로부터...

65 570 [fx-570 ES] 에서 정규 분포 계산하기
세상의모든계산기 2024.09.05 - 11:57 2269 1
통계 관련 계산이 많은 분은 DIST 기능이 빠진 ES 모델보다는, DIST 기능이 추가된 EX 모델을 추천드립니다. [fx-570 ES Plus] 모델은 DIST 기능이 빠져 있지만, 그래도 표준 정규 분포의 확률 계산을 할 수는 있습니다. 변수 데이터 분석을 한 다음에 정규화하여 계산하는 하위메뉴인데, 데이터 입력 없이도 표준 정규 분포 계산에는 활용할 수는 있습니다. (STAT) 여기서 이들 기능을 이용하시면 됩니다. 각각 다음의 계산을 수행합니다. ▶t: 이 함수는 인수 X 뒤에 오며, 정규화된 변량 $ x_{▶t}=\dfrac{X-\overline{x}}{\sigma x} $ 를...

64 570 [fx-570EX] 분포 Distribution. (ES 안됨)
세상의모든계산기 2024.06.18 - 12:01 804 1
1. 분포 Distribution 기능 fx-570 EX 기종부터는 분포 기능이 추가되었습니다. 특정 국가 모델에는 ES PLUS 기종에도 분포 기능이 들어갔지만, 우리나라는 해당사항 없으므로 EX 부터 들어간걸로 치겠습니다. fx-570 EX 에는 분포 모드에서 다음 7개의 함수계산이 가능합니다. Normal PD Normal CD Inverse Normal Binomial PD Binomial CD Poisson PD Poisson CD 2. 계산 예시 표준 정규분포 함수의 누적 분포 함수 (CDF)는 특정 값 이하의 확률을 계산하는 데 사용됩니다. 여기서 Φ(z)는 표준 정규분포의 누적 분포 함수를 나타내며, 이...

63 570 [fx-570 MS] 미분(계수)의 입력 및 계산, Differential Calculation
세상의모든계산기 2015.12.28 - 20:20 5317 1
1. [fx-570 MS] 의 미분기능이란? 도함수를 찾는 기능이 없기 때문에, 엄밀하게는 미분 계수(순간변화율)로 볼 수 없습니다. 엄밀하게는 '아주 짧은 구간(△x)에서의 함수의 평균 변화율을 구하는 기능'이라고 보는 것이 맞는 듯 합니다. 계산기 입력 순서 f'(a)=f(a+∆x)-f(a)∆x=d/dx(f(x),a,∆x) △x 는 직접 지정할 수도 있고, 생략할 수도 있습니다. 생략하면 계산기가 적절한 값으로 대체하여 계산하므로, 그냥 생략하시는 것이 좋겠습니다. 불연속구점이나 변화가 큰 값에서는 오차가 발생할 수 있습니다. 삼각함수에서는 각도 설정을 반...

62 570 계산 이력 (History, Entry) 및 재사용(수정)
세상의모든계산기 2024.08.28 - 11:25 281 1
1. 계산 이력 계산기 화면의 상단에 있는 상태 표시줄에 다음의 아이콘 ▲▼ 이 표시되는 경우가 있습니다. ▲ : 현재 화면의 계산식에 앞서 계산한 이력 있음 ▼ : 현재 화면의 계산식에 다음에 계산한 이력 있음 각각 해당하는 방향키를 누르면 화면이 스크롤되며 이력을 확인할 수 있습니다. 주의 : 계산 이력 데이터는 다음의 경우 전부 삭제될 수 있습니다. -【On】버튼을 누를 때 - 다른 계산 모드로 변경할 때 - Input/Output 표시 설정을 변경할 때 - Reset 조작시 (Initialize All / Setup Data) 2. 계산 이력 재사용 (수정) 계산 이...

61 공통 [fx-350] [fx-570] 계산기 메모리 리셋 초기화 Reset, Initializing
세상의모든계산기 2015.08.13 - 13:01 32317 2
계산기를 사용하다 보면 어느 순간 예상과 다른 결과를 내놓을 때가 있습니다. 그 원인을 잘 모르겠다면, 가장 먼저 시도해 볼 수 있는 것이 바로 기기 초기화 입니다. 초기화는 각종 설정(=Setup)이나 변수값(=Memory)을 기본값으로 바꿉니다. 일부분을 선택해서 초기화할 수도 있고, 전부를 한꺼번에 초기화할 수도 있습니다. 정답은 없고 본인에게 맞는 방법을 선택하시면 되겠습니다. 1. MS 기종 (fx-350, 570 공통) 대상 기종 fx-82MS / 85MS / 300MS / 350MS / 82SX PLUS / 220 PLUS : fx-570MS : 기타 MS 카피 버전 : 다이소 공학용...

60 570 Syntax Error 발생 이유와 대처방법
세상의모든계산기 2024.08.09 - 11:44 1599
Casio fx-570 계산기의 3대 ERROR "Syntax Error" 입력식에서 '문법적 오류'가 발생하였음 "Math Error" 입력식에서 '수학적 오류'가 발생하였음 "Stack Error" 계산 공간이 꽉차서(식이 너무 길어서) 더이상 입력받을 수 없음. 1. 잘못된 수식 구문: - 괄호가 짝이 맞지 않거나 잘못 배치된 경우. 예를 들어, 열려있는 괄호는 반드시 닫혀 있어야 합니다. - 연산자(+, -, *, /)가 잘못 배치된 경우. 예를 들어, 연산자 두 개가 연속으로 들어가거나 연산자가 피연산자 없이 입력된 경우. 2. 잘못된 함수 사용: - 함수의 인수 개수가 맞지 ...

59 9860 History Function, 계산 이력의 활용
세상의모든계산기 2024.08.06 - 14:19 315 1
fx-9860G 설명서 발췌 및 AI 번역 ■History Function ■ 히스토리 기능 히스토리 기능은 수학 입력/출력 모드에서 계산 표현식과 결과의 기록을 유지합니다. 최대 30개의 계산 표현식과 결과가 유지됩니다. 히스토리 기능에 의해 유지되는 계산 표현식을 편집하고 재계산할 수도 있습니다. 이는 편집된 표현식부터 시작하여 모든 표현식을 재계산합니다. 예시 "1+2"를 "1+3"으로 변경하고 재계산하기 위에 보이는 예시를 따라 다음 작업을 수행하세요. • 답 메모리에 저장된 값은 항상 마지막으로 수행된 계산 결과에 따라 달라집니다. 히스...

58 570 [fx-570 EX] 진수 변환 (10진수 100을 → 2진수로)
세상의모든계산기 2015.08.23 - 12:07 2451 1
[fx-570 EX] 진수 변환 (10진수 100을 → 2진수로) 끝.

57 570 [fx-570] Statistics의 Linear Regression 으로 선형 보간법 결과 구하기
세상의모든계산기 2015.10.07 - 11:16 7304 2
문제 : 온도가 250K 일 때, 엔탈피 값을 보간법(interpolation) 을 이용해 구하시오. fx-570 ES : Linear Regression 기능 이용해 구함. 1. : A+BX 2. DATA 입력 * 3열의 FREQ 는 없어도 됨(없는 것이 Default) 3. 4. 숫자 250 입력 5. 6.

56 공통 [fx-570] [fx-350] Iteration, Newton-Raphson 법으로 계산하기
세상의모든계산기 2015.10.08 - 09:52 2291 2
문제 : Iteration의 일종인 Newton-Raphson 법으로 612의 제곱근을 구하시오. (초기값은 10으로 한다.) 관련 링크 : http://www.allcalc.org/6042 초기값을 입력하여 Ans에 저장 Newton-Raphson 법에 의한 수식을 (손으로!) 완성하여 (계산기에) 입력한다. 을 눌러서 완성된 식을 계산한다. 같은 값이 연속될 때까지 3번 과정을 반복한다. * 570 (EX, ES (PLUS), MS) 350 (EX, ES (PLUS), MS) 모두 가능합니다.

55 9860 [fx-9860G] 함수의 매개변수 버튼 【X,θ,T】 사용방법
세상의모든계산기 2016.04.13 - 21:03 7050 1
1. 변수 버튼 【X,θ,T】 다양한 함수를 사용하는 공학용 계산기의 경우에는 변수를 입력하는 경우가 많습니다. 가장 흔하게는 미지수를 X 로 놓고, 각도 관련해서는 세타 θ, 매개변수로는 t 를 사용하기도 합니다. 자주 사용하는 만큼 버튼이 독립되어 있으면 알파벳 키 【ALPHA】 와 조합할 필요 없이 1click 으로 사용할 수 있기 때문에 매우 편리합니다. ※ 함수 뿐 아니라, 간단히(임시로) 결과값을 저장할 때 사용해도 좋습니다. 2. 변수 변경 방법 눌러봐서 X, θ, T 중에서 본인이 원하는 문자가 입력되면 그대로 쓰시면 됩니다. 원하...

54 570 [fx-570 ES] 수식의 수정 - Insert mode / Overwrite mode (feat. 커서의 모양)
세상의모든계산기 2024.07.20 - 18:30 375
1. 수식의 수정 공학용 계산기는 이미 입력한 수식을 언제라도 수정하여 재활용할 수 있습니다. 그런데 fx-570 ES 에서 이 과정은 입력 모드를 어떻게 설정하였느냐에 따라 달라집니다. 2. Insert and Overwrite Input Mode 2.1) Insert Mode (삽입 모드) : 커서가 세로로 길쭉한 선(┃)으로 깜빡입니다. 새로운 문자가 입력될 때, 현재 커서위치의 왼쪽에 삽입됩니다. 기본(default)설정은 삽입 모드입니다. 2.2) Overwrite Mode (덮어쓰기 모드) : 커서가 바닥에 가로로 길쭉한 선( _ )으로 깜빡입니다. 새로운 문자가 입력될 때, 현재 커...

53 9860 [fx-9860G] 통계 - 선형(1차) 회귀 곡선 구하기 (예제, 보간법)
세상의모든계산기 2016.04.11 - 14:01 9566 11 1
1. 예제 x값이 {2.5, 3.0, 5.0} 이고, y값이 {3.3, 2.0, 6.0} 일 때 선형회귀 곡선(ax+b)의 계수 및 결정 계수(r²) 를 구하려면? 2. 계산기 입력 순서 STAT 모드로 진입 【MENU】【2】 DATA 입력 선형 회귀 방법 선택 【F2】 CALC 【F3】 REG 【F1】 X 【F1】 ax+b

1 2 3 4 5 6 7
/ 7 GO

by OrangeDay

SEARCH

[fx-570][fx-350] (2차) 회귀 분석으로 2변수 (2-Var) 통계 분석 하기

1. 2변수 분석? 2-Var Statistics

2. 회귀 분석(Regression)의 활용

3. 2-Var 통계분석 예제 [fx-570ES]

세상의모든계산기 님의 최근 글

세상의모든계산기 님의 최근 댓글

댓글4