- CASIO 9860
[fx-9860] 행렬에 복소수를 넣어 계산할 수 있나? (=연립방정식 복소수계수/복소수근 구하기)
-
- 2024.09.29 - 22:56 2015.12.03 - 19:09 9652 4
1. [fx-9860G] 모델(II 포함)에서 행렬의 원소에 복소수를 넣을 수 있나?
OS Ver 1.xx 에서는 안됩니다.
행렬 안에 복소수를 강제로 집어 넣으면, 위 스샷처럼 Ma ERROR 메시지를 내뿜습니다.
그렇다면 행렬에서는 복소수를 이용할 방법이 전혀 없을까요?
OS Ver 2.0 이상이라면 가능합니다. 간단하죠. ^^
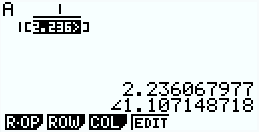
2. 복소수 연립 방정식의 해 - MATRIX & RREF
복소수 계수를 입력할 수만 있다면, 실수 계수인 연립방정식의 해를 찾는 것과 과정은 같습니다.
생성 가능한 행렬 크기에 제약만 없다면, RREF 기능을 사용하는 것이 (입력과정에서는) 가장 효율적입니다.
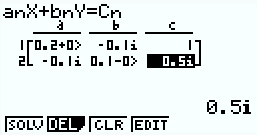
(0.2 + 0.2*i)*v1 + (0−0.1*i)*v2 = 1
(0−0.1*i)*v1 + (0.1-0.1*i)*v2 = 0.5*i
Rref 예시)
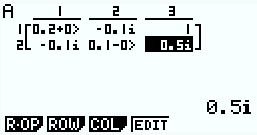
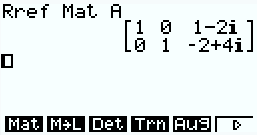
하지만, 결과값이 분수인 경우 Rref 는 분수로 표시하지 못할 가능성이 큽니다.
분수로 결과값을 확인하는 것이 중요한 경우에는 Rref 말고 역행렬 기능을 이용하시는 것이 좋습니다.
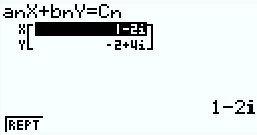
역행렬 예시)
위의 예제에서는
A의 앞(왼쪽) 2×2 부분을 따로 행렬 B에 저장하고, 뒤(오른쪽) 2×1 부분은 행렬 C에 저장합니다.
Mat B-1 × Mat C 을 계산하면 원하는 결과를 얻을 수 있습니다.
-
25
댓글4
-
세상의모든계산기
3원 이상의 연립방정식도 (같은 방법으로) 해를 구해 볼 수 있습니다.
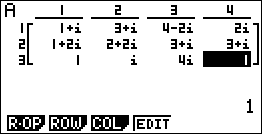
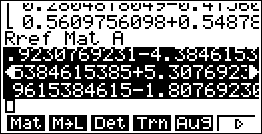
Rref 이용할 때는 해가 항상 소숫점(decimal point) 꼴로만 표시됩니다.
예시문 출처) http://www.hpmuseum.org/forum/archive/index.php?thread-6094.html
정확한 답은 x= (-12-55i)/13, y = (7+69i)/13, z = (25-47i)/26 이며
역함수를 이용할 경우 분수꼴로 표시됩니다. (분수꼴로 표시될 수 있습니다)
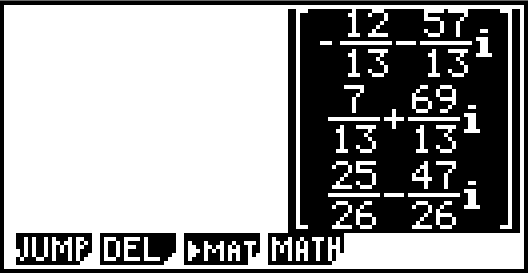
※ 참고 : [TI-nspire] 에서의 결과 http://www.allcalc.org/16404#comment_23848
- 1
세상의모든계산기 님의 최근 댓글
fx-CG 의 경우 분모→A, 분자→B 로 저장해 풀어보면 fx-570 과 같이 A,B,C,D 로 나눠서 계산하면 결과는 둘 다 같음. 73.0495070585238 (15 digits) 같은 15digits 정밀도라도, 공학용 계산기에 따라 결과가 달라질 수 있는 건가? 입력 실수했나? - 어쨌건, TI-nspire 보다 정밀한 결과값 - 파이썬 시뮬레이터상 15 digits 값과 같진 않지만, 유사함. 2025 10.22 [공학용 계산기] 계산기 내부에서 사용하는 유효숫자 자릿수 Significant Digits https://allcalc.org/8848 2025 10.22 계산 정확도 (Internal Precision) 저게 맞나 싶은데요? 무슨 의미로 사용된 용어인지 검증이 필요한 듯 합니다. fx-570 ES PLUS 만 해도 내부 유효자릿수가 15-digits 입니다. https://allcalc.org/55918#comment_55944 2025 10.22 TI-nspire 로 동일하게 A, B, C, D 나누어 계산해 봐도... 한꺼번에 계산한 것과 똑같은 결과 "어? TI-nspire가 유효자릿수가 하나 적나?" 하고 1.234567890123456789 입력하고 Ans - 1.2345678 해 보니 내부 유효자릿수가 다르게 나오네요. TI-nspire 는 (십진수) 14-digits CASIO fx-570 ES 는 (십진수) 15-digits 둘 다 같다고 착각하고 있었나봅니다. 2025 10.22 카시오 fx-570 ES 로 계산하면? 카시오도 (십진수) 14digits 한계이므로, 비슷한 값이 나올 것으로 예상됨. 다만, stack 한계로 한번에 계산이 불가능하므로 부분을 나누어 계산 → A → B → C → D 최종 계산 결과에서 73.049507 을 빼면 fx-570 ES가 구한 결과값(Ans)은 73.0495070584404 (15digits) 로 최종 확인됨. - TI-Nspire 보다 오차가 작음. - 파이썬 시뮬레이션 15 digits 와는 차이가 있음. 2025 10.22