- 세상의 모든 계산기 수학, 과학, 공학 이야기 수학 ()
무게가 서로다른 128개의 물건은 양팔저울로 몇번만에 세번쩨로 무거운물체를 알아낼수 있나요?
-
- 2015.10.16 - 09:30 2015.02.12 - 12:49 1086 1
출처 : http://kin.naver.com/qna/detail.nhn?d1id=11&dirId=1113&docId=218014324&page=1#answer2
네이버 지식인에서 본 문제입니다.
재밌는 것 같으니, 같이 함 풀어봅시다.
-
25
댓글1
-
세상의모든계산기
제가 생각한 방법
1. 1차전
128개를 토너먼트 방식으로 붙여서
가장 무거운 것을 찾습니다. http://ko.wikipedia.org/wiki/싱글_엘리미네이션_토너먼트
이해하기 쉽게 사람이 경기를 하는 것으로 바꾸어 생각해 보겠습니다.
이 때 필요한 경기의 수는
64+32+16+8+4+2+1 = 127 경기2. 2차전
1차전 우승자를 제외시키고,
나머지 중에서 가장 무거운 것을 찾는 2차전을 엽니다.
이 때 참가할 자격이 있는 선수는
1차전 우승자에게 1차전에서 떨어진 자 가 됩니다.
1차전에서 우승자는 결승전 포함하여 총 7경기를 치루어 모두 이겼으니까(7전 7승 무패) 7명이 후보가 있겠고,
각 후보의 전적은 '1전0승1패', '2전1승1패', '3전2승1패', '4전3승1패', ..., '7전6승1패=(1차전 준우승자)'가 됩니다.
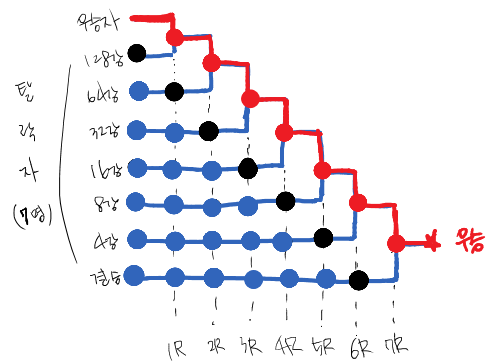
이 7명의 후보를 먼저 떨어진 순서대로 묶어 토너먼트를 치루고, 가장 무거운 돌을 찾습니다.
(1차전 준우승자는 1R 부전승)
이 때는 3+2+1 = 6경기를 치루어야 합니다. 3. 3차전
이제 드디어 세번째 무거운 돌을 가릴 차례가 되었습니다.
3차전 참가자격이 있는 선수는
조건 a = 2차전 우승자(=준우승자)에게 1차전에서 떨어진 자
조건 b = 2차전 우승자(=준우승자)에게 2차전에서 떨어진 자
3 - 경우1. 2차전 우승자가 1차전 준우승자(1차전 전적 7전6승1패)인 경우
a. 1차전 준우승자는 1차전에서 총 7경기를 하였는데, 6번 이기고, 1번(결승전)은 졌으므로, 후보 6명.
b. 2차전에서 (부전승을 제외하고) 2 경기를 하였으므로 후보 2명.
총 후보 8명
경기수 7회3 - 경우2. 2차전 우승자가 4강에서 1차전 우승자에게 떨어진 자일 경우(1차전 전적 6전5승1패)
a. 후보 5명
b. 후보 3명 (총 3경기)
총 후보 8명
경기수 7회3 - 경우 3. 2차전 우승자가 1차전 전적 5전4승1패인 경우
a. 후보 4명
b. 후보 3명
총 후보 7명
경기수 6회3 - 경우 4. 2차전 우승자가 1차전 전적 4전3승1패인 경우
a. 후보 3명
b. 후보 3명
총 후보 6명
경기수 5회3 - 경우 5. 2차전 우승자가 1차전 전적 3전2승1패인 경우
a. 후보 2명
b. 후보 3명
총 후보 5명
경기수 4회3 - 경우 6. 2차전 우승자가 1차전 전적 2전1승1패인 경우
a. 후보 1명
b. 후보 3명
총 후보 4명
경기수 3회3 - 경우 7. 2차전 우승자가 1차전 전적 1전0승1패인 경우
a. 후보 0명
b. 후보 3명
총 후보 3명
경기수 2회4. 결론
따라서 총 저울로 재야하는 횟수는 1차전 횟수 + 2차전 횟수 + 3차전 횟수가 되고
127 + 6 + (2~7) = 135~140 회
최소 135경기, 최대 140경기를 통해 3번째 무거운 돌을 구별해낼 수 있다.
세상의모든계산기 님의 최근 댓글
은행앱 통합하면서 없어졌나보네요. ㄴ 비슷한 기능 찾으시는 분은 : 스마트 금융 계산기 검색해 보세요. https://play.google.com/store/apps/details?id=com.moneta.android.monetacalculator 2026 01.25 Ctrl+Z 를 이용해 뒤로 돌아기기 Undo 기능이 있는지 살펴보세요. 2026 01.23 쌀집계산기로 연립방정식 계산하기 - 크래머/크레이머/크라메르 공식 적용 https://allcalc.org/56739 3. 'x' 값 구하기 계산기 조작법 목표: x = Dx / D = [(c×e) - (b×f)] / [(a×e) - (b×d)] 계산하기 1단계: 분모 D 계산 (메모리 활용) 1 * 1 M+ : 메모리(M)에 1를 더합니다. (현재 M = 1) -0.1 * -0.2 M- : 메모리(M)에서 0.02를 뺍니다. (현재 M = 0.98 = 0.98) 이로써 메모리(MR)에는 분모 0.98가 저장됩니다. 2단계: 분자 Dx 계산 후 나누기 78000 * 1 : 78000를 계산합니다. = : GT에 더합니다. -0.1 * 200000 : -20000를 계산합니다. ± = : 부호를 뒤집어 GT에 넣습니다. // sign changer 버튼 사용 GT : GT를 불러옵니다. GT는 98000 (분자 Dx) 값입니다. ÷ MR = : 위 결과(98000)를 메모리(MR)에 저장된 분모 D(0.98)로 나누어 최종 x값 100,000를 구합니다. 4. 'y' 값 구하기 계산기 조작법 목표: y = Dy / D = [(a×f) - (c×d)] / [(a×e) - (b×d)] 계산하기 1단계: 분모 D 계산 (메모리 활용) 'x'에서와 분모는 동일하고 메모리(MR)에 0.98가 저장되어 있으므로 패스합니다. 2단계: 분자 Dy 계산 후 나누기 GT ± = : GT를 불러오고 부호를 뒤집어 GT에 더합니다. GT가 0으로 리셋됩니다. 【AC】를 누르면 M은 유지되고 GT만 리셋되는 계산기도 있으니 확인해 보세요. 1 * 200000 : 200000를 계산합니다. = : GT에 더합니다. 78000 * -0.2 : -15600를 계산합니다. ± = : 부호를 뒤집어 GT에 넣습니다. GT : GT를 불러옵니다. 215600 (분자 Dy) 값입니다. ÷ MR = : 위 결과(215600)를 메모리(MR)에 저장된 분모 D(0.98)로 나누어 최종 y값 220,000를 구합니다. x, y 값을 이용해 최종 결과를 구합니다. 2026 01.18 크레이머 = 크레머 = 크라메르 공식 = Cramer's Rule https://allcalc.org/8985 2026 01.18 부호 변경, Sign Changer 버튼 https://allcalc.org/52092 2026 01.18