- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
SMPS등 회로 수리시, 뻥 방지 전구(회로) (feat. Chatgpt and deepseek)
뻥방지 전구(과전류 보호 전구)의 원리
SMPS(스위칭 모드 전원 공급 장치) 등의 전기장비 수리 후 테스트할 때 뻥방지 전구를 사용하는 이유는, 수리된 회로에 단락(쇼트) 또는 과부하 문제가 있을 경우 전원 투입 시 즉시 퓨즈가 나가거나 부품이 파손되는 것을 방지하기 위해서입니다.
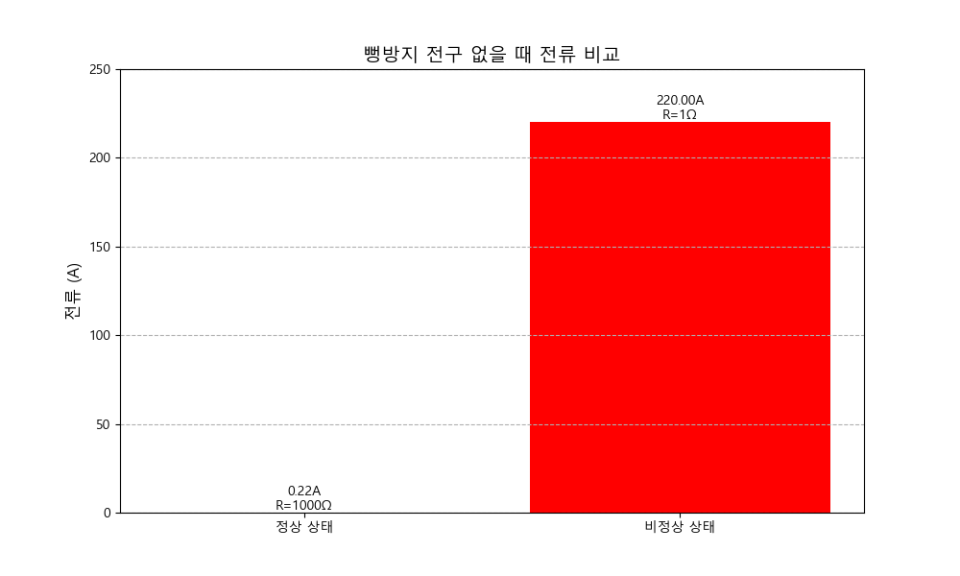
ㄴ 쇼트 등 비정상 상태라서 SMPS 저항값이 1옴일 때를 가정하면, SMPS에 과전류(220A)가 흐르게 됨.
ㄴ 파라미터 V_source = 220 # 공급 전압 220V, R_normal = 1000 # 정상 SMPS 저항(Ω) 1k옴, R_fault = 1 # 비정상 SMPS 저항(Ω)
ㄴ 그래프는 단순 참고용으로, 실제 현실과 다릅니다.
원리 및 동작 방식
-
직렬 연결 방식
- AC 입력 전원과 SMPS 회로 사이에 전구(백열전구)를 직렬로 연결합니다.
- 만약 SMPS가 정상이라면, 전구는 거의 빛나지 않고 미세한 발열만 합니다.
- 만약 쇼트(단락)나 과부하가 있다면, 전구의 필라멘트가 밝게 빛나며 SMPS로 흐르는 전류를 제한합니다.
-
전류 제한 역할
- 뻥방지 전구는 전류가 지나치게 많아지면 저항이 급격히 증가하는 성질을 가집니다.
- 백열전구의 필라멘트는 PTC(Positive Temperature Coefficient) 성질을 가지므로, 과전류가 흐르면 순간적으로 저항이 증가하여 전류를 제한합니다.
- 결과적으로 퓨즈가 끊어지거나 부품이 폭발하는 것을 방지할 수 있습니다.
-
이상 여부 판별
- 전구가 꺼져 있다면 → 정상 동작 (SMPS가 부하를 정상적으로 공급)
- 전구가 순간 깜빡이고 꺼짐 → 정상 (정류 콘덴서 충전 후 정상 동작)
- 전구가 계속 켜져 있음 → 쇼트 가능성 높음 (SMPS 1차측에서 이상 발생)
- 전구가 매우 밝게 빛남 → 심각한 쇼트 (전원 투입 시 과전류 상태)
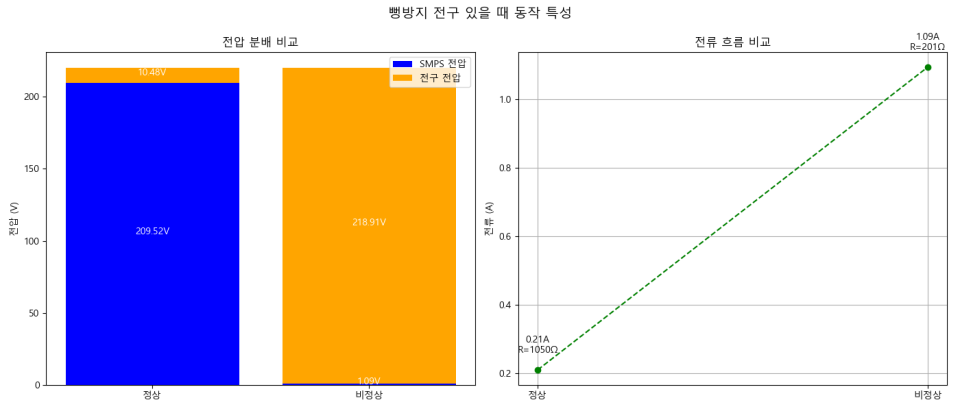
ㄴ 직렬 연결이기 때문에
ㄴ 전압 : 전체 회로에 걸리는 전압은 220V = 전구에 걸리는 전압 + SMPS에 걸리는 전압
ㄴ 전류 : 전구와 SMPS 회로에는 동일한 전류가 흐름.
ㄴ 그래프는 단순 참고용으로, 실제 현실과 다릅니다.
사용하는 전구의 종류
- 일반적으로 100W~200W 백열전구를 사용합니다.
- LED 전구는 이런 특성이 없기 때문에 사용할 수 없습니다.
- 전구의 전력(W)이 높을수록 저항값이 낮아져 초기 테스트 시 주의해야 합니다.
SMPS 수리 후 뻥방지 전구 테스트 절차
- SMPS의 1차측 입력선(AC 전원선)과 직렬로 백열전구를 연결
- 전원을 켜고 전구의 밝기를 확인
- 전구가 순간 깜빡이고 꺼지면 → 정상 작동
- 전구가 계속 밝게 켜지면 → 쇼트나 이상 부품 확인 필요
- 정상 작동을 확인한 후, 전구를 제거하고 직접 AC 입력 테스트 진행
장점
- 과전류로 인한 1차 회로 손상을 방지
- 퓨즈가 연속적으로 끊어지는 것을 막음
- 쇼트 여부를 빠르게 판단 가능
- 간단한 부품(백열전구)만으로 테스트 가능
한계점
- 전구의 저항 특성상 일부 회로에서는 오작동할 가능성 있음
- 고출력 SMPS 테스트 시 너무 낮은 전구 전력 사용 시 동작 불안정. (장비 정상이어도 전구에 불이 켜짐)
- 전구를 지나친 의존하면 근본적인 수리 문제를 놓칠 수도 있음
- 전구와 장비가 전압을 나눠 가지기 때문에 220V에서 정상 운영이 되는지 확인하려면 전구를 반드시 제거하고 테스트를 해야 정확함.
💡 결론:
뻥방지 전구는 SMPS 수리 후 초기 테스트에 유용한 도구이며, 쇼트 및 과부하를 빠르게 진단하는 역할을 합니다. 하지만, 전구를 통한 테스트만으로 모든 문제가 해결되지는 않으므로, 이후 오실로스코프 및 멀티미터를 활용한 추가 점검이 필요합니다.
import matplotlib.pyplot as plt
import numpy as np
# 한글 폰트 설정 (Windows 환경)
plt.rc('font', family='Malgun Gothic') # 맑은 고딕 사용
plt.rc('axes', unicode_minus=False) # 마이너스 기호 깨짐 방지
# 공통 파라미터
V_source = 220 # 공급 전압 220V
R_normal = 1000 # 정상 SMPS 저항(Ω)
R_fault = 1 # 비정상 SMPS 저항(Ω)
R_bulb_normal = 50 # 정상 작동시 전구 저항(Ω)
R_bulb_fault = 200 # 과전류시 전구 저항(Ω)
# 시나리오 1: 뻥방지 전구 없을 때
def scenario1():
I_normal = V_source / R_normal
I_fault = V_source / R_fault
plt.figure(figsize=(10,6))
bars = plt.bar(['정상 상태', '비정상 상태'],
[I_normal, I_fault],
color=['green', 'red'])
plt.ylabel('전류 (A)', fontsize=12)
plt.title('뻥방지 전구 없을 때 전류 비교', fontsize=14)
plt.ylim(0, 25)
# 주석 추가
for bar, label, resistance in zip(bars, ['정상', '비정상'], [R_normal, R_fault]):
height = bar.get_height()
plt.text(bar.get_x() + bar.get_width()/2., height,
f'{height:.2f}A\nR={resistance}Ω',
ha='center', va='bottom')
plt.grid(axis='y', linestyle='--')
plt.show()
# 시나리오 2: 뻥방지 전구 있을 때
def scenario2():
# 정상 상태 계산
I_normal = V_source / (R_normal + R_bulb_normal)
V_smps_normal = I_normal * R_normal
V_bulb_normal = I_normal * R_bulb_normal
# 비정상 상태 계산
I_fault = V_source / (R_fault + R_bulb_fault)
V_smps_fault = I_fault * R_fault
V_bulb_fault = I_fault * R_bulb_fault
# 그래프 생성
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14,6))
# 전압 분배 비교 (스택형 막대 그래프)
labels = ['정상', '비정상']
smps_voltages = [V_smps_normal, V_smps_fault]
bulb_voltages = [V_bulb_normal, V_bulb_fault]
ax1.bar(labels, smps_voltages, color='blue', label='SMPS 전압')
ax1.bar(labels, bulb_voltages, color='orange', bottom=smps_voltages, label='전구 전압')
ax1.set_title('전압 분배 비교')
ax1.set_ylabel('전압 (V)')
ax1.legend()
# 각 전압 수치 표시
for i in range(len(labels)):
ax1.text(i, smps_voltages[i] / 2, f'{smps_voltages[i]:.2f}V', ha='center', color='white', fontsize=10)
ax1.text(i, smps_voltages[i] + bulb_voltages[i] / 2, f'{bulb_voltages[i]:.2f}V', ha='center', color='white', fontsize=10)
# 전류 비교
ax2.plot(labels, [I_normal, I_fault],
marker='o', linestyle='--', color='green')
ax2.set_title('전류 흐름 비교')
ax2.set_ylabel('전류 (A)')
ax2.grid(True)
# 전류 값 및 저항 값 표시
for i, (val, resistance) in enumerate(zip([I_normal, I_fault], [(R_normal + R_bulb_normal), (R_fault + R_bulb_fault)])):
ax2.text(i, val+0.05, f'{val:.2f}A\nR={resistance}Ω', ha='center')
plt.suptitle('뻥방지 전구 있을 때 동작 특성', fontsize=14)
plt.tight_layout()
plt.show()
# 그래프 생성
scenario1()
scenario2()


세상의모든계산기 님의 최근 댓글
자게로 이동조치하였습니다. 그리고 이 글의 내용을 정리하여 HP 포럼에 올려두었습니다. https://allcalc.org/55774 [HP Prime] Solve 함수 사용법 2025 10.27 수치해석 방법 method 를 강제로 선택할 수 있으면 좋을텐데... 위의 스샷을 보면 되는 듯 하면서도 아래 스샷을 보면 안되는 것 같기도 합니다. solve(Expr,[Var]) csolve(LstEq,LstVar) nSolve(Expr,Var,[Guess or Interval],[Method]) deSolve(Eq,[TimeVar],FncVar) linsolve(LstLinEq,LstVar) fsolve(Expr,Var,[Guess or Interval],[Method]) 2025 10.17 종합해서 답변을 드리면 HP Prime 에 solve 에서 변수명에 구간을 입력하면 수치해석 방식으로 bisection 을 사용함. 이 bisection 방식은 해의 좌-우 부호가 서로 바뀌어야만 해를 인식하고 해의 좌-우 부호가 같으면 해를 인식하지 못합니다. 이 때문에 본문 sin 의 예나 아래 사진의 예에서는 해를 인식하지 못하는 것으로 보입니다. 2025 10.17 hp prime 이 solve 함수에서 해를 찾는데 어떤 방법(method)을 사용하는지 공식적인 무서로 정확하게 파악되진 않습니다. 2025 10.17 참고 x=guess 는 iterative 방식(일반적으로는 newton's method를 의미함)을 x=xmin .. xmax 는 bisection 방식을 사용하는 듯 합니다. // 구간지정 개념과는 차이가 있는 듯? 2025 10.17