선박의 아웃리거에 의한 선박 안정성(요동 감쇄)
Reduction Of Outrigger Wide To Maximize Fishing Boat ...
https://iptek.its.ac.id › article › download › pdf_266
2024. 8. 5. — Moreover, broader outriggers can amplify vessel motion, leading to extended oscillation periods, ... of the boat with and without the use ...
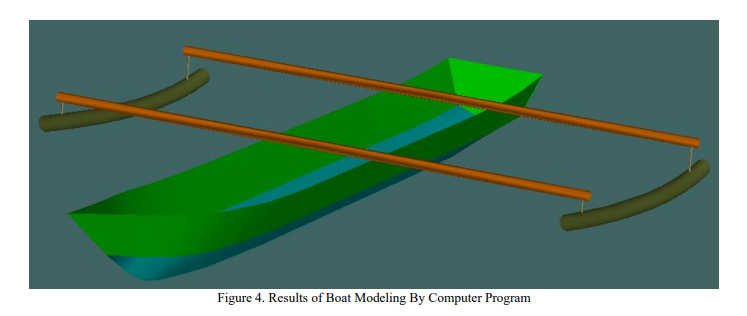
1. 연구 배경:
- 프리기 지역의 주깅(Jukung) 어선들은 넓은 아웃리거(약 5미터) 때문에 해안 가까이 정박하기 어려운 문제가 있습니다.
2. 연구 목적:
- 아웃리거 폭을 줄여 PPN 프리기 항구의 정박 용량을 늘리면서도 선박 안정성을 유지하는 방법을 찾고자 합니다.
3. 연구 방법:
- 다양한 아웃리거 폭(1.5m, 1.25m, 1m, 0.75m)에 대해 선박 안정성을 분석했습니다.
- HSC 2000 Annex 7과 Annex 749 (18) Ch3 설계 기준을 사용했습니다.
4. 주요 결과:
- 아웃리거 폭을 1미터로 줄여도 선박 안정성 기준을 충족합니다.
- 이 변경으로 15미터 정박지에서 정박 효율을 66% 높일 수 있습니다.
- PPN 프리기 동쪽 부두의 주깅 선박 수용량이 142척에서 236척으로 증가합니다.
5. 결론:
- 아웃리거 폭을 줄이면 항구 인프라를 최적화하고 프리기 어업 공동체의 운영 효율성을 향상시킬 수 있습니다.
이 연구는 전통적인 어선 설계를 현대화하여 항구 용량과 효율성을 개선하는 방법을 제시하고 있습니다.
댓글2
-
세상의모든계산기
클로드 Sonnet 3.5에게 수치적으로 분석해 달라고 했습니다.
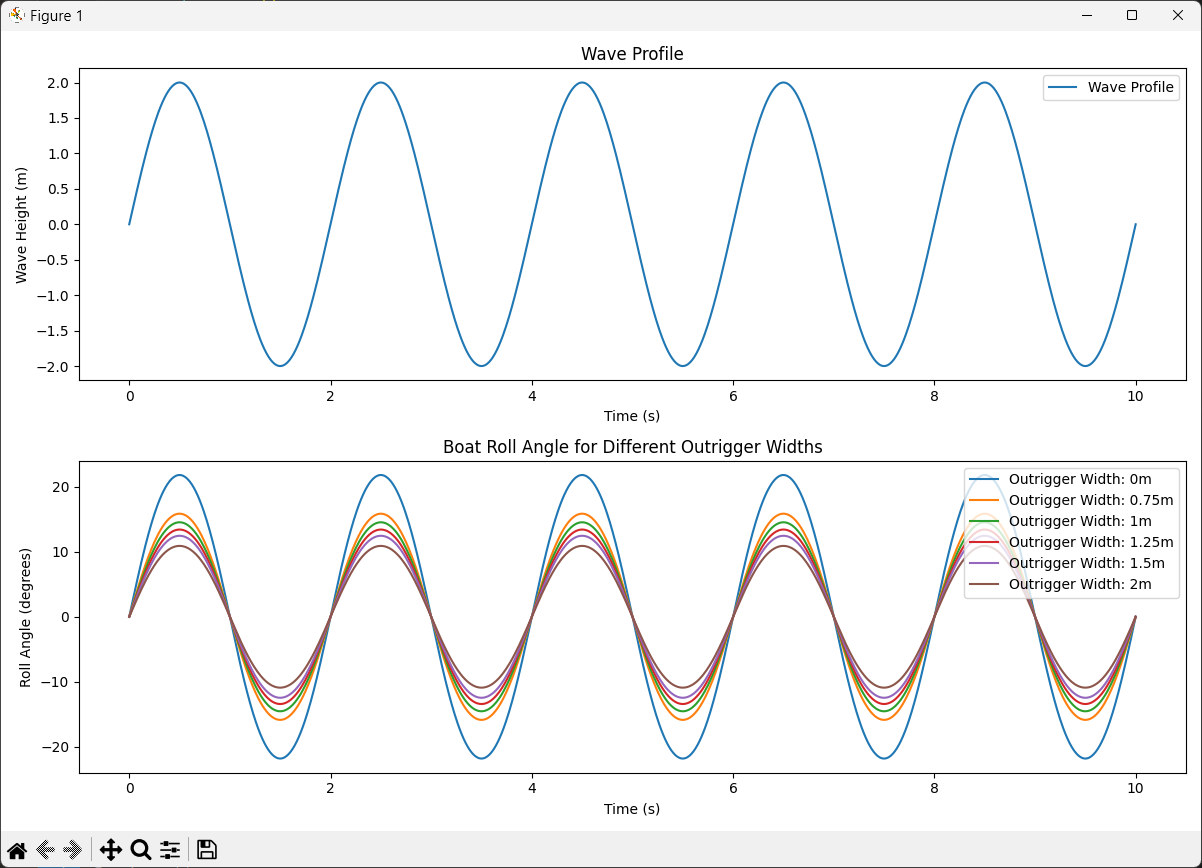
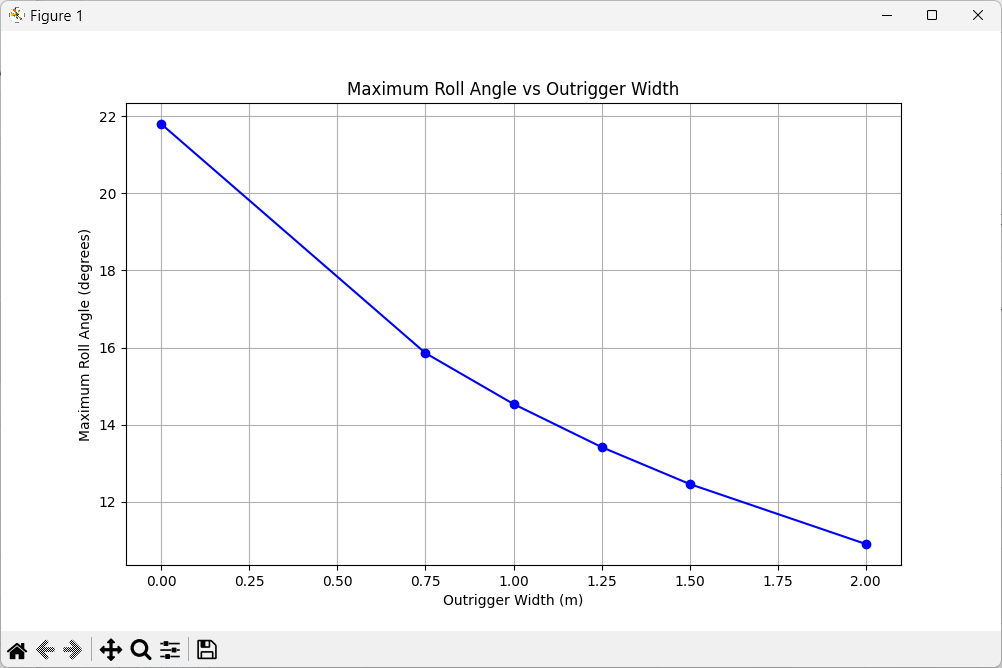
import numpy as np import matplotlib.pyplot as plt from scipy.signal import find_peaks # 파도 프로파일 생성 함수 def generate_wave_profile(time, amplitude, frequency): return amplitude * np.sin(2 * np.pi * frequency * time) # 선박 요동 각도 계산 함수 def calculate_boat_angle(wave_height, outrigger_width): base_angle = np.arctan(wave_height / 5) # 기본 각도 (아웃리거 없을 때) if outrigger_width == 0: return np.degrees(base_angle) else: return np.degrees(base_angle / (1 + outrigger_width * 0.5)) # 아웃리거 효과 # 파라미터 설정 time = np.linspace(0, 10, 1000) # 10초 동안 1000개 데이터 포인트 wave_amplitude = 2 # 파도 진폭 (미터) wave_frequency = 0.5 # 파도 주파수 (Hz) # 파도 프로파일 생성 wave_profile = generate_wave_profile(time, wave_amplitude, wave_frequency) # 아웃리거 폭 범위 설정 outrigger_widths = [0, 0.75, 1, 1.25, 1.5, 2] # 그래프 설정 plt.figure(figsize=(12, 8)) # 파도 프로파일 플롯 plt.subplot(2, 1, 1) plt.plot(time, wave_profile, label='Wave Profile') plt.title('Wave Profile') plt.xlabel('Time (s)') plt.ylabel('Wave Height (m)') plt.legend() # 선박 요동 각도 플롯 plt.subplot(2, 1, 2) for width in outrigger_widths: boat_angles = [calculate_boat_angle(h, width) for h in wave_profile] plt.plot(time, boat_angles, label=f'Outrigger Width: {width}m') plt.title('Boat Roll Angle for Different Outrigger Widths') plt.xlabel('Time (s)') plt.ylabel('Roll Angle (degrees)') plt.legend() plt.tight_layout() plt.show() # 최대 요동 각도 분석 max_angles = [] for width in outrigger_widths: boat_angles = [calculate_boat_angle(h, width) for h in wave_profile] peaks, _ = find_peaks(boat_angles) max_angle = np.mean(np.array(boat_angles)[peaks]) max_angles.append(max_angle) # 최대 요동 각도 플롯 plt.figure(figsize=(10, 6)) plt.plot(outrigger_widths, max_angles, 'bo-') plt.title('Maximum Roll Angle vs Outrigger Width') plt.xlabel('Outrigger Width (m)') plt.ylabel('Maximum Roll Angle (degrees)') plt.grid(True) plt.show() # 결과 출력 for width, max_angle in zip(outrigger_widths, max_angles): print(f"Outrigger Width: {width}m, Max Roll Angle: {max_angle:.2f} degrees")인공지능 정말 똑똑하네요.
인공지능은 아직 개발 초기단계라는거...


세상의모든계산기 님의 최근 댓글
[fx-570 ES] 과학 상수를 이용한 계산에서 에러 발생 상황 https://kin.naver.com/qna/detail.naver?d1id=11&dirId=1118&docId=492235162&page=1&answerNo=1 vs 2026 03.01 과학상수를 이용한 계산 중 자릿수 한계로 인한 에러 발생 가능성 https://allcalc.org:443/board_calculators/6925#comment_57029 2026 03.01 기본 어댑터 MODEL : AD0301-1202500GB INPUT : 100~240V, 50~60Hz, 0.8A Max OUTPUT : 12.0V, 2.5A, 30.0W ㄴ 측정시 플러그 외경/내경 : 5.5mm / 2mm 2026 02.15 엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10 엑셀 / 행의 최대 개수, 열의 최대 개수, 셀의 최대 개수 엑셀의 행 개수 제한은 파일 형식에 따라 다르며, 최신 .xlsx 파일 형식은 시트당 최대 1,048,576행까지 지원하지만, 구형 .xls 파일은 65,536행으로 제한됩니다. 따라서 대용량 데이터를 다룰 때는 반드시 최신 파일 형식(.)으로 저장해야 하며, 행과 열의 총 수는 1,048,576행 x 16,384열이 최대입니다. 주요 행 개수 제한 사항: 최신 파일 형식 (.xlsx, .xlsm, .xlsb 등): 시트당 1,048,576행 (2^20). 구형 파일 형식 (.xls): 시트당 65,536행 (2^16). 그 외 알아두면 좋은 점: 최대 행 수: 1,048,576행 (100만여개) 최대 열 수: 16,384열 (XFD) 대용량 데이터 처리: 65,536행을 초과하는 데이터를 다루려면 반드시 .xlsx 형식으로 저장하고 사용해야 합니다. 문제 해결: 데이터가 많아 엑셀이 멈추거나 오류가 발생하면, 불필요한 빈 행을 정리하거나 Inquire 추가 기능을 활용하여 파일을 최적화할 수 있습니다. 2026 02.10