- 세상의 모든 계산기 자유(질문) 게시판 팁 & 정보 ()
DNS Benchmark 프로그램
1. DNS?
DNS란 Domain Name System 의 약자로서 도메인 주소에 대한 IP 주소를 매칭하여 알려주는 시스템(서버)입니다.
대부분의 사람들이 그러하듯 그냥 신경 안쓰고 자동(Auto)으로 두면, OS는 자기가 속한 ISP 의 DNS Server 를 선택합니다. 공유기를 사용한다면 공유기를 DNS Server로 선택하기도 합니다. 공유기는 Default 로 자기가 속한 ISP 의 DNS Server 에서 DNS 정보를 가져오니까 거기서 거기라고 볼 수도 있겠네요.
그런데 DNS 서버마다 반응속도가 다를 수도 있고, (의도적이거나/비의도적이거나) 잘못된 IP주소를 주는 경우도 있습니다. 그래서 DNS Server를 잘 선택하는 것은 생각보다 중요한 문제일 수도 있습니다.
2. DNS Benchmark 프로그램
그래서 DNS 성능을 알아보려고 하는데... DNS Server 주소를 하나씩 바꿔 가면서 테스트 해볼 수는 없는 노릇이고... 그런데 웹을 뒤적여 보니 쓸만한 프로그램이 하나 있습니다.
https://www.grc.com/dns/benchmark.htm
Gibson Research Corporation 이라는 곳에서 만든 프로그램인데, 개인 프리랜서 같기도 하고... 잘은 모르겠네요.
일단 Virustotal.com 의 검사 결과로는 문제없는 파일로 보입니다.
3. Benchmark 실행 결과
※ Nameservers
국내 ISP 의 DNS Server 들이 포함되어 있지 않아서 Add로 주소들을 추가해 주고 Run Benchmark
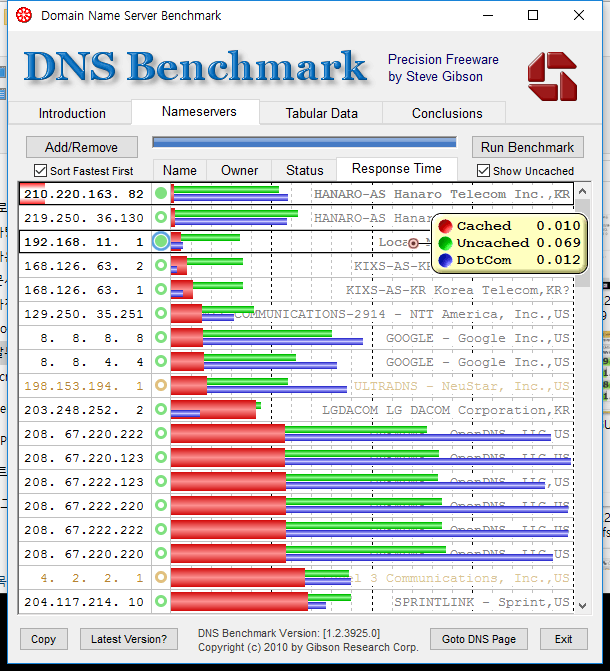
※ 결과 해석
- 벤치마크 걸린 시간 : 대략 4분
- 그래프가 짧을 수록 빠름(=좋음)
- 빨강=Cached(이미 있는 정보) / 초록=Uncached(신규 정보, Sub-domain) / 파랑=DotCom(??)
Dotcom lookups – the time to consult the nameserver's chosen dotcom resolver(s) for a dotcom name. - Sort Fastest First 체크하니 빨강이 짧은 순서대로 나열이 됩니다.
- 공유기와 KT DNS 가 상위권을 차지하였습니다.
- 의외로 Hanaro DNS 가 1위를 차지하였습니다. 이유는 잘 모르겠습니다.
※ Tabular Data
여기를 클릭하면 상세한 정보가 나옵니다.
Final benchmark results, sorted by nameserver performance:
(average cached name retrieval speed, fastest to slowest)
210.220.163. 82 | Min | Avg | Max |Std.Dev|Reliab%|
----------------+-------+-------+-------+-------+-------+
- Cached Name | 0.002 | 0.003 | 0.004 | 0.000 | 100.0 |
- Uncached Name | 0.005 | 0.107 | 0.286 | 0.064 | 95.9 |
- DotCom Lookup | 0.006 | 0.116 | 0.204 | 0.062 | 100.0 |
---<-------->---+-------+-------+-------+-------+-------+
bns1.hananet.net
HANARO-AS Hanaro Telecom Inc.,KR
219.250. 36.130 | Min | Avg | Max |Std.Dev|Reliab%|
----------------+-------+-------+-------+-------+-------+
- Cached Name | 0.003 | 0.004 | 0.005 | 0.001 | 100.0 |
- Uncached Name | 0.005 | 0.126 | 0.298 | 0.083 | 100.0 |
- DotCom Lookup | 0.007 | 0.115 | 0.176 | 0.062 | 100.0 |
---<-------->---+-------+-------+-------+-------+-------+
bns2.hananet.net
HANARO-AS Hanaro Telecom Inc.,KR
192.168. 11. 1 | Min | Avg | Max |Std.Dev|Reliab%|
----------------+-------+-------+-------+-------+-------+
+ Cached Name | 0.001 | 0.010 | 0.123 | 0.021 | 100.0 |
+ Uncached Name | 0.004 | 0.069 | 0.206 | 0.048 | 100.0 |
+ DotCom Lookup | 0.003 | 0.012 | 0.112 | 0.024 | 100.0 |
---<OOOO---->---+-------+-------+-------+-------+-------+
dd-g300n
Local Network Nameserver
168.126. 63. 2 | Min | Avg | Max |Std.Dev|Reliab%|
----------------+-------+-------+-------+-------+-------+
- Cached Name | 0.001 | 0.016 | 0.145 | 0.039 | 100.0 |
- Uncached Name | 0.003 | 0.072 | 0.218 | 0.052 | 100.0 |
- DotCom Lookup | 0.002 | 0.006 | 0.116 | 0.016 | 100.0 |
---<-------->---+-------+-------+-------+-------+-------+
kns2.kornet.net
KIXS-AS-KR Korea Telecom,KR
168.126. 63. 1 | Min | Avg | Max |Std.Dev|Reliab%|
----------------+-------+-------+-------+-------+-------+
- Cached Name | 0.001 | 0.022 | 0.216 | 0.047 | 100.0 |
- Uncached Name | 0.002 | 0.072 | 0.190 | 0.051 | 100.0 |
- DotCom Lookup | 0.003 | 0.012 | 0.117 | 0.027 | 100.0 |
---<-------->---+-------+-------+-------+-------+-------+
kns.kornet.net
KIXS-AS-KR Korea Telecom,KR?
※ Conclusion
여기에서는 비록 영어긴 하지만, DNS 서버 설정관련한 추천(Recommendation)을 해 주고 있습니다.

괜찮은 항목은 [V] 표시가 뜨고, 문제(또는 개선의 여지)가 있는 항목은 저렇게 [X] 표시가 뜹니다.
자신의 컴퓨터 환경에 관심이 있는 한번 해볼만한 테스트인 것 같습니다.


세상의모든계산기 님의 최근 댓글
3×3 이상인 행렬의 행렬식 determinant https://allcalc.org/50536 2025 12.30 답에 이상한 숫자 14.2857142857가 들어간 것은 조건식에 소숫점(.) 이 들어가 있기 때문에 발생한 현상이구요. 100÷7 = 14.285714285714285714285714285714 소숫점 없이 분수로 식이 주어졌을 때와 결과적으로는 동일합니다. 2025 12.30 그럼 해가 무한히 많은지 아닌지 어떻게 아느냐? 고등학교 수학 교과과정에 나오는 행렬의 판별식(d, determinant)을 이용하면 알 수 있습니다. ㄴ 고교과정에서는 2x2 행렬만 다루던가요? 연립방정식의 계수들로 행렬을 만들고 그 행렬식(determinant)을 계산하여야 합니다. 행렬식이 d≠0 이면 유일한 해가 존재하고, d=0 이면 해가 없거나 무수히 많습니다. * 정상적인 경우 (`2y + 8z = 115`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 8 | 행렬식 값 = 1(0 - (-7)) - 1(8 - 0) = 7 - 8 = -1 (0이 아니므로 유일한 해 존재) * 문제가 된 경우 (`2y + 7z = 100`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 7 | 행렬식 값 = 1(0 - (-7)) - 1(7 - 0) = 7 - 7 = 0 (0이므로 유일한 해가 존재하지 않음) 2025 12.30 좀 더 수학적으로 말씀드리면 (AI Gemini 참고) 수학적 핵심 원리: 선형 독립성(Linear Independence) 3원 1차 연립방정식에서 미지수 x, y, z에 대한 단 하나의 해(a unique solution)가 존재하기 위한 필수 조건은 '주어진 세 개의 방정식이 서로 선형 독립(linearly independent) 관계에 있어야 한다'는 것입니다. * 선형 독립 (Linearly Independent): 어떤 방정식도 다른 방정식들의 조합(상수배를 더하거나 빼는 등)으로 만들어질 수 없는 상태입니다. 기하학적으로 이는 3개의 평면(각 방정식은 3D 공간의 평면을 나타냄)이 단 한 개의 점(해)에서 만나는 것을 의미합니다. * 선형 종속 (Linearly Dependent): 하나 이상의 방정식이 다른 방정식들의 조합으로 표현될 수 있는 상태입니다. 이 경우, 새로운 정보를 제공하지 못하는 '잉여' 방정식이 존재하는 것입니다. 기하학적으로 이는 3개의 평면이 하나의 선에서 만나거나(무수히 많은 해), 완전히 겹치거나, 혹은 평행하여 만나지 않는(해가 없음) 상태를 의미합니다. 질문자님의 사례는 '선형 종속'이 되어 무수히 많은 해가 발생하는 경우입니다. 2025 12.30 질문하신 연립 방정식은 미지수가 3개이고 모두 1차인 3원 1차 연립방정식입니다. 이상적으로 문제가 없다면 {x,y,z} 에 대한 좌표가 하나 나오게 됩니다. 원하는 답 {52.5, -2.5, 15} 그런데 '두개 조건(식)을 그대로 두고 나머지 하나를 변형하다 보니, 원하는 답이 나오지 않는 상황이 발생하였다.'고 질문하신 상황입니다. 3개의 조건식이 주어진 3원 1차 연립방정식은 조건을 변형해서 하나의 변수를 제거할 수 있습니다. 그러면 2개의 조건식으로 주어지는 2원 1차 연립방정식으로 변형이 됩니다. ㄴ 꼭 변형해야하는 것은 아니지만, 이것이 알아보기 쉽기 때문에 변형시키는 것입니다. 변경하지 않은 2개 조건의 식(con1) 을 이용해 위와 같이 하나의 y & z 1차 방정식을 유도할 수 있는데요. 변경하는 나머지 1개의 방정식이 con1에서 유도된 방정식과 동일하다면 하나의 답이 구해지지 않는 상황이 발생하는 것입니다. 계산기(ti-nspire)는 {x,y,z} 의 답이 하나가 아니고 무수히 많음을 c1 을 이용해서 표현해 준 것입니다. linear_independence_cond12.tns 2025 12.30