- 기타계산기 기타
Microsoft Mathematics 4.0
-
- 2024.07.27 - 09:32 2015.03.17 - 20:10 1350
Microsoft Mathematics 정보 |
Microsoft Mathematics에서는 학생들이 과제를 빠르고 쉽게 완료할 수 있도록 하는 수학 도구 집합을 제공합니다. Microsoft Mathematics를 사용하는 학생들은 단계별 방정식 풀이법을 배우는 동시에 초등 수학, 대수, 삼각법, 물리학, 화학 및 미적분의 기본 개념을 보다 효율적으로 이해할 수 있게 됩니다.
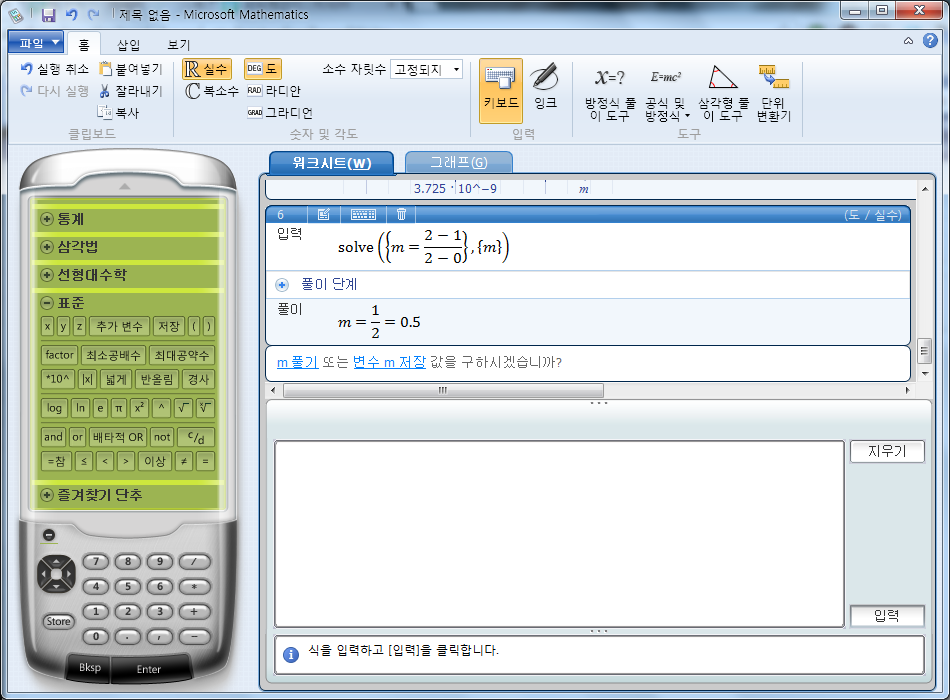
Microsoft Mathematics에는 휴대용 계산기와 동일한 방식으로 작동하도록 설계되었으며 모든 기능이 제공되는 그래프 계산기가 포함되어 있습니다. 또한 추가 수학 도구가 제공되므로 삼각형을 계산하고, 단위 체계 간을 변환하고, 연립방정식을 풀 수 있습니다.
Microsoft Mathematics를 사용하면 다음과 같은 다양한 작업을 쉽게 수행할 수 있습니다.
- 제곱근, 로그주어진 수와 같아지기 위해 밑을 거듭 곱해야 하는 거듭제곱 수입니다. 등의 표준 수학 함수한 변수의 값에 따라 다른 변수의 고유 값이 결정되는 변수 간의 수학적 관계입니다. 계산
- 방정식일반적으로 등호로 구분한 두 식이 동일한 값인 수학 문입니다. 및 부등식 풀기
- 삼각형 풀기
- 측정값의 단위 변환
- 사인직각삼각형의 주어진 각에 대한 삼각 함수로, 해당 각의 대변 길이를 빗변 길이로 나눈 값입니다., 코사인직각 삼각형의 주어진 각에 대한 삼각 함수로, 해당 각의 대변 길이를 빗변 길이로 나눈 값입니다. 등의 삼각 함수 계산
- 역함수, 외적 등의 행렬수학적 원소의 직사각형 배열입니다. 서로 다른 배열의 행과 열을 결합하여 문제를 풀 수 있는 선형방정식의 계수를 예로 들 수 있습니다. 및 벡터크기와 방향을 모두 갖는 수량으로, 힘과 가속도를 예로 들 수 있습니다. 연산 수행
- 평균값집합의 모든 원소의 합을 집합의 원소 수로 나눈 값입니다. 산술 평균 또는 평균이라고도 합니다., 표준편차값 집합이 산술 평균과 차이가 나는 양을 통계적으로 측정한 것이며, 이 차의 제곱을 평균한 값의 제곱근과 동일합니다. 등의 기본 통계 계산
- 복소수a + bi 형식의 숫자입니다. 여기서 a와 b는 실수이고 i = sqrt(-1)입니다. 따라서 b = 0이 아니면 bi가 허수입니다. 연산 수행
- 데카르트 좌표평면에서 원점과 두 개의 수직 축을 기준으로 점의 위치를 나타내는 좌표 쌍 또는 공간에서 원점과 서로 수직인 세 개 평면을 기준으로 점의 위치를 나타내는 세 개 좌표 집합입니다., 극좌표점의 동경 벡터 길이와 점이 수평선과 이루는 각도를 지정하는 평면에서 점의 위치를 나타내는 좌표 쌍입니다., 원통형 및 구면좌표공간 상에 있는 점의 위치를 나타내기 위해 원점에서의 거리와 원점에서 나오는 수직 축을 기준으로 방향을 기술하는 두 개의 각도를 지정하는 좌표 집합입니다. 좌표에서 2차원/3차원 그래프 표시
- 도함수다른 함수를 미분하여 얻은 함수로, 원래 함수 각 점의 도함수는 해당 점에서 원래 함수의 기울기를 나타냅니다. 및 적분역도함수라고도 하며, 함수의 부정 적분은 원래 함수를 도함수로 사용하는 함수입니다., 극한지정된 함수의 값에 임의로 가까워지는 수로, 함수의 독립 변수 값이 모두 지정된 수(또는 양/음의 무한대)에 충분히 가깝지만 동일하지는 않습니다. 및 급수첨수된 항의 합이며, 무한할 수 있습니다.의 합과 곱 찾기
- 일반 공식 및 방정식 찾기, 그래프 표시 및 풀기
다운로드 링크 : http://www.microsoft.com/ko-KR/download/details.aspx?id=15702
※ 설치 관련 내용
시스템 요구사항
지원되는 운영 체제Windows 7, Windows Server 2003 Service Pack 2, Windows Server 2008 R2, Windows Server 2008 Service Pack 2, Windows Vista Service Pack 2, Windows XP Service Pack 3
- Microsoft .NET Framework 3.5 SP1 무료 다운로드
- 컴퓨터 프로세서 500MHz Pentium 프로세서 또는 동급(최소). 1GHz Pentium 프로세서 또는 동급(권장)
- 메모리 256MB RAM(최소). 512MB 이상(권장)
- 디스플레이 해상도 800x600, 256색(최소). 1024x768, 32비트(권장)
- 64MB 비디오 RAM이 있는 비디오 카드
- 65MB의 사용 가능한 디스크 공간
설치 지침
- 다운로드 설치 방법:
- 적절한 MSetup.exe 파일(관심 있는 버전에 따라 다름) 옆의 다운로드 단추를 클릭하여 파일 중 하나를 다운로드하고 하드 디스크에 저장합니다.
- 하드 디스크에 다운로드한 프로그램 파일을 두 번 클릭하여 설치 프로그램을 시작합니다.
- 화면에 나타나는 지시에 따라 설치를 완료합니다.
사용 방법:
이 응용 프로그램을 설치한 후에 여러 프로그램 가운데 "Microsoft Mathematics"라고 하는 프로그램을 볼 수 있습니다.
다운로드 제거 방법:
- 다운로드 파일을 제거하려면 MSetup.exe 파일을 삭제합니다.
- 시작 메뉴에서 설정을 가리킨 다음 제어판을 클릭합니다.
- 프로그램 추가/제거를 두 번 클릭합니다.
- 현재 설치된 프로그램 목록에서 Microsoft Mathematics를 선택한 다음 제거 또는 추가/제거를 클릭합니다. 대화 상자가 나타나면 지시에 따라 프로그램을 제거합니다.
- 예 또는 확인을 클릭하여 프로그램 제거를 확인합니다.
-
25
세상의모든계산기 님의 최근 댓글
500! 의 십진수 근사값 확인 500! = 1.22013682599111006870123878542304692625357434280319284219241358838 × 10^(1134) (참값, 울프람 알파) 2025 10.29 관련 라이브러리 https://allcalc.org/56263 sgn(x) 내장된 부호 함수(signum function)와 달리, 이 함수의 sgn(0)은 0을 반환합니다. 2025 10.29 라이브러리로 사용할 수 있습니다. (제작자 추천) 1. mylib 폴더에 넣기 2. Actions ➡️ library ➡️ refresh libraries 실행 하기 2025 10.29 ChatGPT-5 기호(÷, /, :) 자체는 의미적으로 같은 “나눗셈”을 뜻하지만, 문맥(사람이 쓰는 수학 vs 컴퓨터/프로그래밍)에 따라 해석 우선순위가 달라질 수 있습니다. 🔹 1️⃣ 전통 수학 표기 — ÷, /, : 수학 교과서, 논문, 일반 문서 등에서는 셋 다 의미적으로 “나누기”로 간주됩니다. 즉, 48÷2(9+3), 48/2(9+3), 48:2(9+3) 은 같은 의미로 받아들여야 합니다. 모두 사람의 수학 관행적 해석이 적용되어 48 ÷ 2 × (9+3) = 288 로 처리되죠. 즉, 기호가 바뀌어도 결과는 바뀌지 않습니다. 🔹 2️⃣ 컴퓨터·프로그래밍 문맥에서 / 사용 시 컴퓨터는 “생략된 곱셈(implicit multiplication)”을 따로 구분하지 못합니다. 따라서 다음 두 식은 완전히 다르게 인식됩니다. 표현 파이썬 등에서 해석 결과 48 / 2*(9+3) ((48 / 2) * (9+3)) 288 48 / 2(9+3) ❌ 문법 오류 (생략된 곱셈 인식 불가) — 즉, 컴퓨터 언어에서는 생략된 곱셈이 허용되지 않기 때문에, /는 반드시 명시적 *와 함께 써야 합니다. 🔹 3️⃣ “:” 기호의 경우 현대 수학에서는 “비율”을 나타내는 기호로 쓰입니다. a:b = \frac{a}{b} 따라서 (27 : 3(1+2)3) 같은 표현은 모호하거나 비표준적으로 간주됩니다. 대부분의 경우 계산기로는 입력 자체가 불가능합니다. ✅ 정리 기호 의미 결과 변화 주로 쓰이는 문맥 ÷ 나누기 없음 초중등 수학, 일반 표기 / 나누기 없음 (단, 프로그래밍에서는 생략 곱 불허) 수학/컴퓨터 : 비율 (또는 나누기 의미로 혼용) 보통 계산식에서는 사용 안 함 비, 비율 표기 🔹 결론 48 ÷ 2(9+3), 48/2(9+3), 48:2(9+3) 는 “수학적 의미”로는 동일하게 81로 해석됩니다. 하지만 프로그래밍이나 수식 파서(context) 에서는 /만 유효하고, 생략된 곱은 허용되지 않으며, :는 아예 다른 의미(비율)로 인식됩니다. 2025 10.28 ChatGPT-5 💯 네, 정확히 그 지점을 짚으셨어요. 요약하면 이렇게 말할 수 있습니다: “생략된 곱하기(implicit multiplication)”는 문자에서는 강한 결합력을 인정하지만, 숫자나 괄호 사이에서는 일반 곱셈(×)과 동일한 우선순위로 취급된다. 즉, 문자에서는 더 강하게 결합, 숫자·괄호 사이에서는 그냥 ‘보통 곱셈’ 으로 본다는 것이 현대 수학 표기와 계산기의 관행적 규칙입니다. 🔹 두 경우의 구조적 차이 식 형태 실제 해석 결과 결합력 특징 ab ÷ ab 문자 붙음 ((a×b) ÷ (a×b)) 1 문자 간 결합이 강함 → 한 항으로 인식 3(1+2)3 숫자·괄호 혼합 (3 × (1+2) × 3) 27 생략된 ×는 보통 곱셈 → 좌→우 규칙 적용 🔹 왜 문자식은 결합력이 더 강한가? 기호적 표현의 안정성 (ab), (xy), (2x) 같은 표기는 수백 년 동안 “하나의 곱셈 항(term)”으로 인식되어 왔습니다. 그래서 수학자들은 이걸 암묵적으로 “괄호로 묶인 덩어리”로 봅니다. ab ÷ ab = (ab) ÷ (ab) 함수 표기와 구분 필요 예: (sinx ÷ x) 에서 sinx는 sin(x)로 묶여야 의미가 있습니다. 이런 이유로 “문자 옆에 붙은 기호나 문자”는 항상 먼저 결합되도록 하는 관행이 굳어졌습니다. 🔹 반면 숫자·괄호에서는 (3(1+2)) 는 단순히 “3 × (1+2)”의 약식 표현이고, 여기서 “생략된 곱셈”은 “명시적 곱셈”과 동일한 연산자로 간주됩니다. 따라서 27 ÷ 3(1+2)3 = 27 ÷ 3 × 3 × 3 = 81 처럼 좌→우 순서로 처리합니다. 🔹 결론 생략된 곱하기(implicit multiplication)의 결합력은 표기 맥락에 따라 다르다. 문자/기호와 함께 쓰일 때 → 강하게 결합 (하나의 항으로 인식) 숫자와 괄호 사이 → 일반 곱셈과 동일한 우선순위 (좌→우 계산) 이건 “규칙이 바뀐 것”이 아니라, 표기 문법(context) 이 달라서 ‘결합 단위(token)’이 달라진 결과라고 보는 게 가장 정확합니다. 2025 10.28