- TI BA II Plus
[BA II Plus] TVM Solver 기능 이용하기
1. TVM Solver 란?
재무용 계산기의 중심에 있는 기능은 바로 TVM Solver 입니다. 공학용 계산기의 solver() 기능과 유사하지만, 재무계산TVM(Time Value of Money)에 특화된 solver 이기 때문에, 필수적인 숫자(N, I/Y, PV, PMT, FV)만 입력하면 답이 나옵니다. 따라서 공학용 계산기의 solver() 보다 훨씬 편리합니다.
PMT가 일정액이 아니고 매 기 변화하는 조건일 때는 TVM Solver 가 아니라 CF 기능(NPV, IRR)을 사용합니다.
관련 글 : http://www.allcalc.org/8551
2. 변수값의 입력 (중요)
필수변수 : N, I/Y, PV, PMT, FV
위의 5개 변수가 기본이자 필수적인 변수입니다. 이 중에서 알고있는 4개의 값을 입력하면, 미지의 변수 1개의 값을 계산해낼 수 있습니다. 변수간 입력 순서는 중요하지 않습니다만, 최종 계산하려는 변수는 마지막에 계산해야겠죠?
- 기본값 : 0
- 입력할 때 순서 : 【숫자】【변수】
- (미지수) 계산할 때 순서 : 【CPT】【변수】
보조변수 : C/Y, P/Y, BGN&END
- 기본값 : 1, END
- 월납, 분기납 등의 조건 & 명목, 실질 이자율 관련하여 C/Y, P/Y 를 수정할 수 있습니다.
하지만 그냥 1로 놓고 쓰시는 것을 추천합니다.
이자율이 월/분기 단위로 나오는데 그 값을 ×12 또는 ×4 또는 ×2 를 곱해서 년 단위 (표시)이자율을 구할 수 있습니다.
※ DATA 초기화 : 【2ND】【CPT】【2ND】【FV】
- 필수변수 4개를 입력하고 다른 1개의 값을 찾는 것이 보통이므로 계산과정에서 자료가 overwrite(덮어쓰기) 되긴 하지만, 시작할 때 모두 초기화 하는 것이 좋습니다.
음수의 입력 방법 : 【+|-】 버튼 활용
- 위 버튼은 숫자 3 아래 위치하고 있고, -(neg)를 의미하는 기호가 아니고, 음양부호(sign)을 change 하는 명령입니다.
- 따라서, (기호)
 (숫자)의 순서가 아니고, (숫자)
(숫자)의 순서가 아니고, (숫자) (부호변경)의 순서로 입력합니다.
(부호변경)의 순서로 입력합니다. - (나를 기준으로) 현금이 손에 들어오면 +, 돈이 손에서 나가면 - 로 놓습니다.
3. 예시
3-1. PMT 구하기
※ 이자율 10%일 때, 10000원을 빌려서 5년간 동일한 금액을 갚아나가려 한다. 매년 갚을 금액은?
필수 변수
| N | I/Y | PV | PMT | FV |
| 5 | 10 | 10000 | 구하려는 값 | 0 |
버튼 입력 순서
【5】【N】【10】【I/Y】【10000】【PV】【0】【FV】
【CPT】【PMT】
결과 화면
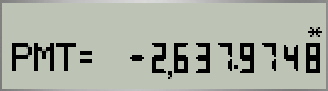
상세 설명
- 5개 변수값은 기본값이 0이므로, 여기서 【0】【FV】 는 생략해도 됩니다. (CLR TVM 했다고 가정할 때)
- 수중에서 돈이 빠져나가므로 마이너스(-)가 붙음
3-2. PV 구하기
※ $2,000,000의 기계를 구입하여 운용하면, 향후 5년간 매년 $600000 의 현금흐름이 발생할 것으로 기대되는 투자가 있다. 연 이자율이 10%일 때 투자가치(NPV)는? (5년말 기계 회수액은 없다)
필수 변수
| N | I/Y | PV | PMT | FV |
| 5 | 10 | 구하려는 값 | 600000 | 0 |
버튼 입력 순서
【5】【N】【10】【I/Y】【600000】【PMT】【0】【FV】
【CPT】【PV】
결과 화면
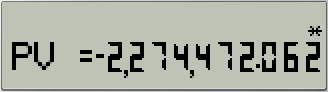
상세 설명
- 5개 변수값은 기본값이 0이므로, 여기서 【0】【FV】 는 생략해도 됩니다. (CLR TVM 했다고 가정할 때)
- 이자율 10% 일 때 매년 말 $600,000 의 수입을 얻기 위해서는, 현재(Present) $2,274,472 를 지출해야 합니다.
- 그런데 기계구입에 쓰는 돈은 $2,000,000 뿐이므로, 원래 필요한 돈($2,274,472)보다 적은 돈으로 수입을 만들어 낸 것이니 좋은 투자안이고, 그 차액만큼이 투자가치가 됩니다. ($2,274,472-$2,000,000=$274,472)
- 차액 계산하지 않고 투자가치를 그냥 한번에 구하려면, TVM Solver 말고 CF NPV 기능을 이용하는 것이 좋습니다.
3-3. I/Y (=이자율) 구하기
※ 액면가액 10,000원인 3년만기 무이표채의 현재가격이 \8,638.38일 때, 만기수익률은?
필수 변수
| N | I/Y | PV | PMT | FV |
| 3 | 구하려는 값 | -8638.38 | 0 | 10000 |
버튼 입력 순서
【3】【N】【8638.38】【+|-】【PV】【10000】【FV】
【CPT】【I/Y】
결과 화면

상세 설명
- 현재(Present) 채권구입을 위해 돈이 나가므로 (-), 미래(Future)에 돈이 들어오므로 (+) 로 설정합니다.
- 반대 입장을 가정하여 PV와 FV의 부호를 서로 바꾸어도 상관은 없습니다.
- 무이표채이므로 PMT=0 입니다. 기본값과 같으므로 입력을 생략합니다.


세상의모든계산기 님의 최근 댓글
approx(참 해) 값이 이상하게 튀는 것 같아서 wolfram alpha 로 구해보려고 했는데 수식 길이가 너무 길다고 거부하는 바람에 AI를 이용해서 구해본 것입니다. 참 해가 계산 과정이 너무 길다보니 오차가 누적되어 적절한 해의 x 구간을 벗어나버린 듯 합니다. 2025 10.21 그래프로 확인 그래프 함수로 지정하고, 매우 좁은 구간으로 그래프를 확대해 보면 불연속적인 그래프 모습이 확인됩니다. 이것은 한계 digits(15자리) 이상을 처리하지 못하기 때문일 것이구요. 다만 특이한 점은, 그래프상으로 교점에 해당하는 구간이 73.049507058477≤x≤73.049507058484 사이로 나오는데 -> 이 구간은 'solve에서 여러 방법으로 직접 구해진 해들'은 포함되는 구간입니다. -> 하지만, '참값인 해를 계산기로 구한 appprox 값 x=73.049507058547'은 포함되지 않는 구간입니다. 2025 10.21 tns 파일 첨부 sol_num_vs_exact.tns 2025 10.21 검증하면 1번 식을 x에 대해 정리하고, → 그 x 값을 2번 식에 대입해 넣으면 → 그 결과로 x는 사라지고 y에 대한 식이 되니, y에 대해 정리하면 참값 y를 얻음. 얻은 y의 참값을 처음 x에 대해 정리한 1번식에 대입하면 참 값 x를 얻음. 구해진 참값의 근사값을 구하면 x=73.049507058547 and y=23.747548955927 어떤 solve로 나온 근사값이든, 계산기로 구한 참값의 근사값(=approx(참값)) 이든 원래의 식 모두(ext1 and ext2) 를 만족시킬 수 없음. 그런데 AI로 구한 참값의 numeric 근사값은 두 식을 만족시킴 ! 유레카 2025 10.21 그렇다면 해의 참 값은? 먼저, 모든 decimal 값을 유리수로 변환하고, solve 로 답을 구함. 변수 x로는 구해지는데 y로는 "Error: Resource exhaustion" 발생 // 이유는 모름. approx(exsol1) x=73.049507058547 and y=23.747548955927 2025 10.21