모기지 상환 비율 (원리금 균등 분할 상환 조건)

댓글3

• 0

  세상의모든계산기

  2024.10.11 - 02:27 2024.10.11 - 01:49 #49596

  문제 예시) 

  ---

  홍길동은 주택을 구입하면서 주택 담보 대출을 받았다.

  대출액 5억원, 연 이자율 4%, 20년 만기, 매년 말 원리금 균등 분할 상환 조건이다. 

  5년 후 미상환 원금 잔액(bal)은?

   

  상환 테이블 

  

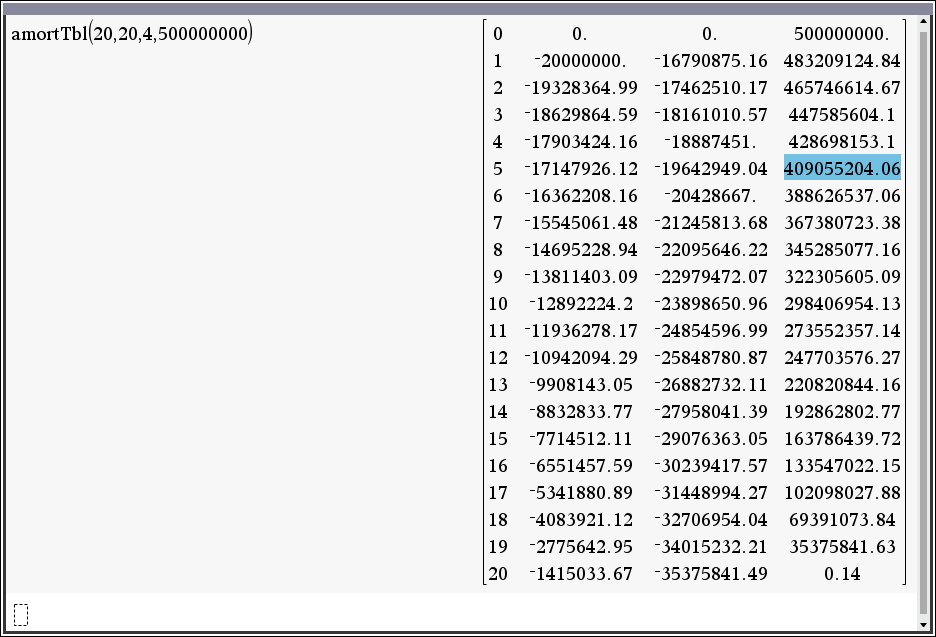
  ㄴ 차례대로 : 기수(기말), 상환 이자액, 상환 원금, 미상환 원금 잔액

   

  $ \frac{(1+0.04)^{5}-1}{(1+0.04)^{20}-1} = 0.18188959190924 = \text {상환 비율} $

  미상환 비율 = 1- 0.18188959190924 = 0.81811040809076

  미상환 원금 잔액 = 미상환 비율 * 대출원금 = 409,055,204

  Attached file

  image.png 58.6KB 19

  댓글
• 0

  세상의모든계산기

  2024.10.11 - 02:42 2024.10.11 - 02:03 #49601

  매년 말 1회 원리금 균등 분할 상환 방식으로 대출을 상환할 경우, t년 후 상환비율을 계산하는 식은 다음과 같습니다.

  ---

  1. 기본 개념

  대출 원금 \( L \)에 대해 연이자율 \( r \)와 상환 기간 \( n \)년이 주어졌을 때, 매년 상환하는 금액 \( A \)는 다음과 같이 계산됩니다:

  \[
  A = \frac{L \cdot r \cdot (1 + r)^n}{(1 + r)^n - 1}
  \]

   

  2. t년 후 잔여 원금

  원리금 균등 분할 상환 방식에서는 매년 상환 금액의 일부가 이자와 원금으로 나누어지며, 시간이 지남에 따라 잔여 원금이 줄어듭니다.

  t년 후 잔여 원금 \( B_t \)는 다음과 같은 공식을 통해 계산됩니다.

  잔여 원금 \( B_t \)는 \( t \)년 동안 상환한 금액을 고려한 후 남은 원금입니다:

  \[
  B_t = L \times \frac{(1 + r)^n - (1 + r)^t}{(1 + r)^n - 1}
  \]

   

  3. t년 후 상환된 원금

  t년 후 상환된 원금은 총 원금 \( L \)에서 잔여 원금 \( B_t \)를 뺀 값으로 구할 수 있습니다:

  \[
  \text{상환된 원금} = L - B_t
  \]

  이를 \( B_t \) 식에 대입하면:

  \[
  \text{상환된 원금} = L - L \times \frac{(1 + r)^n - (1 + r)^t}{(1 + r)^n - 1}
  \]

  이 식을 정리하면:

  \[
  \text{상환된 원금} = L \left( 1 - \frac{(1 + r)^n - (1 + r)^t}{(1 + r)^n - 1} \right)
  \]

  \[
  = L \times \frac{(1 + r)^t - 1}{(1 + r)^n - 1}
  \]

   

  4. 상환비율

  상환비율은 t년 후 상환된 원금을 대출 원금 \( L \)에 대한 비율로 나타낸 것입니다. 따라서 상환비율은 다음과 같이 표현됩니다:

  \[
  \text{상환비율} = \frac{\text{상환된 원금}}{L} = \frac{L \times \frac{(1 + r)^t - 1}{(1 + r)^n - 1}}{L}
  \]

   

  5. 최종 상환비율 공식

  결과적으로 t년 후 상환비율은 다음과 같이 표현됩니다:

  \[
  \text{상환비율} = \frac{(1 + r)^t - 1}{(1 + r)^n - 1}
  \]

  이 식은 t년 동안 상환된 원금이 전체 대출 원금에서 차지하는 비율을 나타내며, 원리금 균등 분할 상환 방식의 특성을 잘 반영하고 있습니다. 

  댓글
• 0

  세상의모든계산기

  2024.10.11 - 02:44 2024.10.11 - 02:25 #49605

  모기지 (Mortgage)?

  ---

  모기지는 주택을 구매하거나 차환하기 위해 돈을 빌리는 것을 허용하고 빌린 돈을 갚지 못할 경우 대출 업체가 귀하의 부동산을 소유할 수 있는 권리를 부여하는 귀하와 대출 업체 간의 계약입니다.

   

  Time Value of Money 6계수에서 MC(저당 상수)가 Mortgage Constant 의 약자입니다. 

  댓글