- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
안티로그 Antilog 가 뭐지?? 첨 들어봤넹...
웹을 검색하다가 "안티로그"라는 단어를 처음 보게 되었습니다.

뭔가 로그에 대한 비난을 쏟아낼 것 같은 느낌이 들어서 움찔했는데,
그냥 '상용로그의 역함수'이더라구요.
(간혹 자연로그의 역함수로 설명하기도 합니다. 그냥 로그의 역함수로 보면 될 듯.)
![]() 괜히 쫄았네.ㅎ
괜히 쫄았네.ㅎ
"Antilog"는 수학에서 로그의 역연산을 의미합니다.
기본적으로 로그는 어떤 수가 특정한 밑에 대해 몇 번 곱해져서 다른 수가 되는지 찾는 과정입니다.
이때 antilog는 그 과정을 거꾸로 하는 작업으로, 주어진 로그 값으로부터 원래의 숫자를 구하는 것입니다.
예시
- 만약 우리가 \( \log_{10}(x) = 2 \)라는 값을 가지고 있다면, 이는 10을 몇 번 곱했을 때 \(x\)가 되는지 알려줍니다.
- \( \log_{10}(x) = 2 \)는 \( x = 10^2 \), 즉 \( x = 100 \)이 됨을 의미합니다.
- 이때 \(100\)을 "antilog"라고 부를 수 있습니다.
일반식
주어진 로그 값 \( y \)에 대해, 밑 \( b \)에 대한 antilog는 \( b^y \)입니다.
- 예를 들어, \( y = 3 \)이고 \( b = 2 \)인 경우, antilog는 \( 2^3 = 8 \)이 됩니다.
계산기에서 antilog 사용
일반 계산기에서는 보통 \(10^x\) 또는 \(e^x\) 키를 사용하여 10진수나 자연 로그의 antilog를 계산할 수 있습니다.
댓글4
-
세상의모든계산기
Logarithm Table (로그 테이블)
https://maths.forkids.education/antilog-log-table-how-to-use-see-value/
Download Print-Friendly PDF Version:
File 1 (1 to 50)
and
File 2 (51 to 99)
-
세상의모든계산기
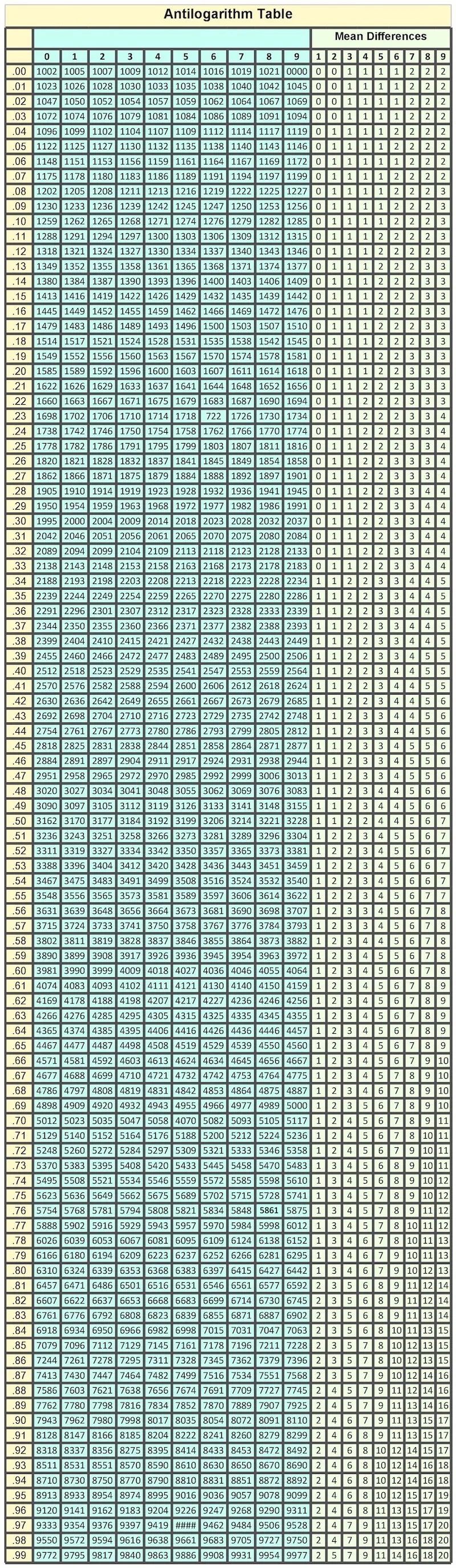
Antilogarithm Table (안티로그 테이블)
Download Print Friendly Antilog Table PDF File:
and
-
세상의모든계산기
log(k)= 1.5629228687415 에서 k 를 구할 때
말씀하신 내용을 반영하여 주어진 로그 값 \(\log_{10}(k) = 1.5629228687415\)에서 \(k\) 값을 정확하게 찾는 방법을 다시 설명드리겠습니다.
1. 정수 부분과 소수 부분 분리:
\[
\log_{10}(k) = 1.5629228687415
\]
여기서 정수 부분은 1이고, 소수 부분은 0.5629228687415입니다.2. 소수 부분을 두 자리로 반올림:
소수 부분 0.5629228687415을 두 자리로 반올림하면 0.56이 됩니다.3. 안티로그 표에서 0.56 찾기:
안티로그 표의 세로축에서 0.56을 찾습니다. 해당 행에서 첫 번째 열의 값은 3631입니다.
4. 소수 부분의 세 번째 자리 반영:
소수 부분의 세 번째 자리는 2입니다. 0.56 행의 두 번째 열(0.562에 해당)을 찾아야 합니다. 이 값은 3648입니다.5. 소수 부분의 네 번째 자리 반영:
소수 부분의 네 번째 자리는 9입니다. Mean Differences 열에서 9에 해당하는 값을 찾습니다. 이 값은 8입니다.6. 값 더하기:
안티로그 표의 0.562에 해당하는 값인 3648에 Mean Differences의 9에 해당하는 값 8을 더합니다:
3648 + 8 = 3656안티로그표의 값은 원래의 값을 1000배 한 값이므로, 원래값은 ÷1000 으로 구할 수 있습니다.
따라서 소수부분에 해당하는 값은 $ 10^{0.5629228687415} = 3.656 $ 입니다.
7. 정수 부분 반영:
\[
k = 10^{1.5629228687415} = 10^1 \times 10^{0.5629228687415}
\]정수 부분 1을 반영하기 위해 \(10^1\)을 곱합니다:
\[
k = 10^1 \times 3.656 = 10 \times 3.656 = 36.56
\]따라서 최종적으로 주어진 로그 값 \(\log_{10}(k) = 1.5629228687415\)에서 \(k\) 값을 구하면, \(k \approx 36.56\)이 됩니다.


세상의모든계산기 님의 최근 댓글
예시11) 선형 연립방정식에서 답이 false 로 나올 때 https://allcalc.org/55823 2025 10.22 approx(참 해) 값이 이상하게 튀는 것 같아서 AI를 이용해 (python 으로) 구해보았습니다. * python 의 유효자릿수가 nspire 의 유효자릿수(14자리~15자리)보다 더 길기 때문에 시도하였습니다. ** 원래는 wolfram alpha 로 구해보려고 했는데, 울프람에서는 수식 길이가 너무 길다고 거부하는 바람에 포기하였습니다. 그 결과, AI approx(참 해) 값은 정상 범주에 포함되었고, 이는 solve()로 구한 대부분의 결과값과 유사하였습니다. 그럼 nspire 의 approx(참 해)는 왜 튀었나? 참 해에 더하기,빼기,곱하기,나누기 가 너무 많이 포함되어 있다보니, 모두 계산하고 나면 오차가 누적&증폭되어 버리는 것 같습니다. 그래서 오히려 solve의 numeric 한 접근보다도 더 큰 오차가 발생한 듯 하고, 그래서 적절한 해의 x 구간을 벗어나버린 듯 합니다. 그것이 처음의 solve 에서 false 를 이끌어낸 주 원인이 아니었을까요? (추정) 2025 10.21 그래프로 확인 그래프 함수로 지정하고, 매우 좁은 구간으로 그래프를 확대해 보면 불연속적인 그래프 모습이 확인됩니다. 이것은 한계 digits(15자리) 이상을 처리하지 못하기 때문일 것이구요. 다만 특이한 점은, 그래프상으로 교점에 해당하는 구간이 73.049507058477≤x≤73.049507058484 사이로 나오는데 -> 이 구간은 'solve에서 여러 방법으로 직접 구해진 해들'은 포함되는 구간입니다. -> 하지만, '참값인 해를 계산기로 구한 appprox 값 x=73.049507058547'은 포함되지 않는 구간입니다. 2025 10.21 tns 파일 첨부 sol_num_vs_exact.tns 2025 10.21 검증하면 1번 식을 x에 대해 정리하고, → 그 x 값을 2번 식에 대입해 넣으면 → 그 결과로 x는 사라지고 y에 대한 식이 되니, y에 대해 정리하면 참값 y를 얻음. 얻은 y의 참값을 처음 x에 대해 정리한 1번식에 대입하면 참 값 x를 얻음. 구해진 참값의 근사값을 구하면 x=73.049507058547 and y=23.747548955927 참 값을 approx() 로 변환한 근사값은 원래 방정식 모두를 만족할 수 없지만, linsolve() 로 찾은 근사값과, AI로 참 값을 근사변환한 값은 원래 방정식 모두를 만족할 수 있습니다. 2025 10.21