- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
자기 포텐셜 -> 점의 자속밀도는? feat. curl
질문
전류 분포가 벡터 자기 포텐셜 A[Wb/m] 를 발생시킬 때,
점 (-1,2,5)[m] 에서의 자속 밀도 B[T]는?
(단, A=2yz^2ax + y^2xay+4xyzaz 이다)
답변
문제는 주어진 벡터 자기 퍼텐셜 \( \mathbf{A} \)에서 자속 밀도 \( \mathbf{B} \)를 계산하는 것입니다. 벡터 자기 퍼텐셜 \( \mathbf{A} \)는 다음과 같이 주어져 있습니다:
\[ \mathbf{A} = 2yz^2 \mathbf{a_x} + y^2 x \mathbf{a_y} + 4xyz \mathbf{a_z} \]
자속 밀도 \( \mathbf{B} \)는 벡터 자기 퍼텐셜 \( \mathbf{A} \)의 회전(curl)로 계산할 수 있습니다:
\[ \mathbf{B} = \nabla \times \mathbf{A} \]
회전 연산자의 정의는 다음과 같습니다:
\[ \begin{vmatrix}
\mathbf{a_x} & \mathbf{a_y} & \mathbf{a_z} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
A_x & A_y & A_z
\end{vmatrix} \]
여기서 \( A_x = 2yz^2 \), \( A_y = y^2 x \), \( A_z = 4xyz \)입니다.
이를 행렬식으로 계산하면:
\[ \nabla \times \mathbf{A} = \mathbf{a_x} \left( \frac{\partial (4xyz)}{\partial y} - \frac{\partial (y^2 x)}{\partial z} \right) - \mathbf{a_y} \left( \frac{\partial (4xyz)}{\partial x} - \frac{\partial (2yz^2)}{\partial z} \right) + \mathbf{a_z} \left( \frac{\partial (y^2 x)}{\partial x} - \frac{\partial (2yz^2)}{\partial y} \right) \]
각 항을 계산하면:
-
\( \mathbf{a_x} \) 항:
$ \frac{\partial (4xyz)}{\partial y} = 4xz , \frac{\partial (y^2 x)}{\partial z} = 0 $
$ \text{따라서, } \mathbf{a_x} \text{ 항은 } 4xz \mathbf{a_x} $
-
\( \mathbf{a_y} \) 항:
$ \frac{\partial (4xyz)}{\partial x} = 4yz , \frac{\partial (2yz^2)}{\partial z} = 4yz $
$ \text{따라서, } \mathbf{a_y} \text{ 항은 } (4yz - 4yz) = 0 $
-
\( \mathbf{a_z} \) 항:
$ \frac{\partial (y^2 x)}{\partial x} = y^2 , \frac{\partial (2yz^2)}{\partial y} = 2z^2 $
$ \text{따라서, } \mathbf{a_z} \text{ 항은 } (y^2 - 2z^2) \mathbf{a_z} $
따라서 자속 밀도 \( \mathbf{B} \)는 다음과 같습니다:
\[ \mathbf{B} = 4xz \mathbf{a_x} + (y^2 - 2z^2) \mathbf{a_z} \]
이 값을 점 \( (-1, 2, 5) \)에서 계산하면:
- \( x = -1 \)
- \( y = 2 \)
- \( z = 5 \)
$ \mathbf{B} = 4(-1)(5) \mathbf{a_x} + (2^2 - 2(5)^2) \mathbf{a_z} $
$ \mathbf{B} = -20 \mathbf{a_x} + (4 - 50) \mathbf{a_z} $
$ \mathbf{B} = -20 \mathbf{a_x} - 46 \mathbf{a_z} $
댓글1
-
세상의모든계산기
TI-nspire CAS 를 이용한 풀이
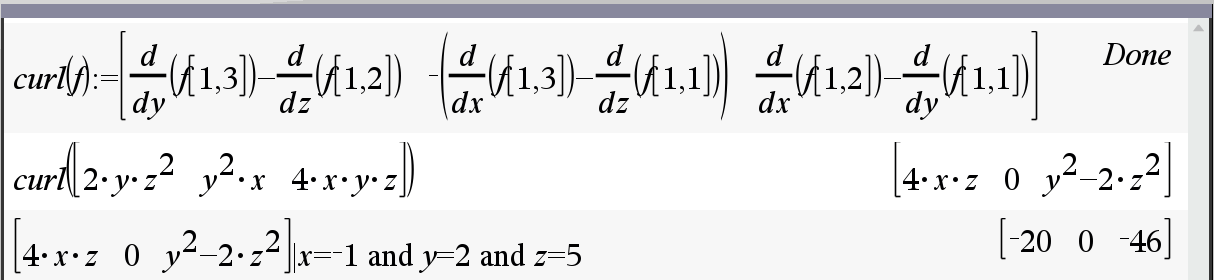
curl([2*y*z^(2),y^(2)*x,4*x*y*z])|x=−1 and y=2 and z=5
의 방식으로는 풀이가 되지 않습니다.
입력하면 오답 [0 0 0] 이 나옵니다.


세상의모든계산기 님의 최근 댓글
일반 계산기는 일반적으로 세팅이나 리셋기능이 따로 없기 때문에, 다른 요인에 영향을 받을 가능성은 없어 보이구요. '원래는 잘 되었는데, 지금은 설정 값이 날아간다'면 메모리 값을 유지할만큼 배터리가 꾸준하게 공급되지 않기 때문일 가능성이 높다고 봐야겠습니다. - 태양광이 있을 때는 계산은 가능하지만, 서랍등에 넣으면 배터리가 없어서 리셋 https://blog.naver.com/potatoyamyam/223053309120 (교체 사진 참조) 1. 배터리 준비: * 다이소 등에서 LR54 (LR1130) 배터리를 구매합니다. (보통 4개 들이 1,000원에 판매됩니다. LR44와 높이가 다르니 혼동하시면 안됩니다.) 2. 준비물: * 작은 십자드라이버 (계산기 뒷면 나사용. 이것도 없으시면 다이소에서...) 3. 커버 분해: * 계산기 뒷면의 나사를 풀고, 머리 부분(윗부분)의 커버를 조심스럽게 분해합니다. (참고해주신 블로그 사진을 보시면 이해가 빠르실 겁니다.) 4. 배터리 교체: * 기존 배터리를 빼냅니다. * 새 LR54 배터리의 '+'극 방향을 정확히 확인하여 제자리에 넣어줍니다. (대부분의 경우 '+'극이 위로 보이도록 넣습니다.) 5. 조립: * 커버를 다시 닫고 나사를 조여줍니다. * 블로그 사진을 보니 배터리 연결선 등이 눌려서 씹혀 있네요. 원래 씹히도록 설계를 안하는데, 원래 그렇게 만들어 놓은 건지? 모르겠네요. 여튼 씹히면 단선될 가능성이 있으니, 잘 보시고 플라스틱 틈새 등으로 적절히 배치해서 안씹히게 하는 것이 좋습니다. 6. TAX 재설정: * 계산기의 전원을 켜고 TAX 요율을 10%로 다시 설정합니다. 2025 12.10 TI-nspire 입력 방법 solve({x+a+b=5,x)|a=1 and b=2 2025 12.01 질문하실 때는 항상 계산기 모델명을 정확하게 적으셔야 합니다. 2025 12.01 참고 - [공학용 계산기] 로그의 입력 (log, ln) (feat. 밑 입력이 안되는 계산기는?) https://allcalc.org/14995 2025 11.14 HP-39gII 에 ExistOS 설치하기 https://allcalc.org/38526 2025 11.07