• SEARCH

    통합검색
세모계
    • Dark Mode
    • GNB Always Open
    • GNB Height Maximize
    • Color
    • Brightness
    • SINCE 2015.01.19.
    • 세모계 세모계
    •   SEARCH
    • 세상의 모든 계산기
      • 자유(질문) 게시판
      • 계산기 뉴스/정보
      • 수학, 과학, 공학 이야기
      • 세모계 : 공지 게시판
        • 구글 맞춤검색
    • TI
    • CASIO
    • HP
    • SHARP
    • 일반(쌀집) 계산기
    • 기타계산기
    • by OrangeDay
  • TI
    • TI nspire

    • [TI-nspire] 연립방정식 풀기 - 역행렬 / RREF / linsolve

    • Profile
      • 세상의모든계산기
      • 2018.08.14 - 08:40 2016.03.24 - 18:50 22014 2

    1. 연립방정식

    연립방정식 및 그 풀이방법에 대해서는 아래 링크를 확인해주세요.

    http://www.allcalc.org/14534

     

    아래에서는 행렬을 이용해서 연립방정식 예제를 풀어보도록 하겠습니다.

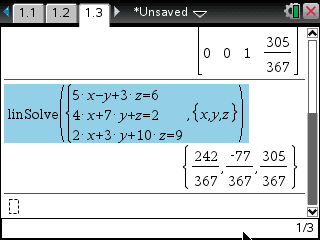
    5x1 - x2 + 3x3 = 6
    4x1 + 7x2 + x3 = 2
    2x1 + 3x2 + 10x3 = 9

     

    2. 역행렬 이용

    1. ​【9】오른쪽의 템플릿 버튼을 눌러서 템플릿창을 띄웁니다.
      03-24-2016 Image004-32p.png
      3×3 이상의 행렬은 3칸짜리를 선택
       
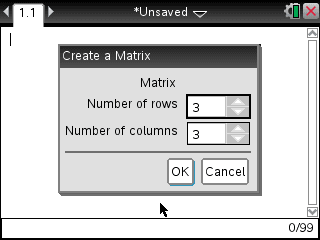
    2. 행과 열을 입력
      03-24-2016 Image005-32p.png
       
    3. 행렬의 각 칸에 요소를 입력하고 a에 저장
      우변의 상수항은 c에 저장
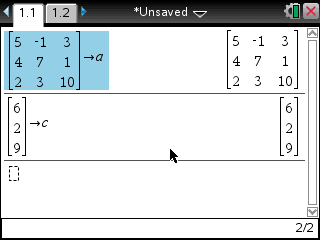
      03-24-2016 Image006-32p.png
      변수에 저장하지 않아도 계산은 가능은 하지만, 재사용할 때 편리하게 사용하려면 변수에 저장하는 것이 좋습니다.
       
    4. a와 c를 이용해서 계산을 합니다. 
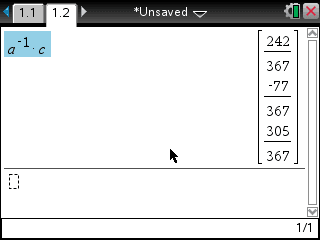
      03-24-2016 Image007-32p.png
      역행렬은 【^】【(-)】【1】 로 입력합니다. 

     

    3. RREF 이용

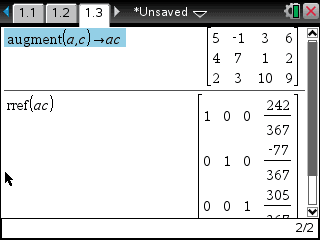
    1. a 행렬과 c 행렬을 하나로 합칩니다.
      새로 3×4 행렬을 만들어도 됩니다.  
       
    2. rref 로 기약행사다리꼴을 만듭니다. 
      rref 명령은 메뉴버튼에도 포함되어 있습니다. 
      03-24-2016 Image011-32p.png03-24-2016 Image010-32p.png

     

    4. linsolve

    1. linsolve() 는 선형(1차) 연립방정식 전용 solve 함수입니다. 
      03-24-2016 Image012-32p.png
       
    2. 방정식의 갯수를 지정합니다. 
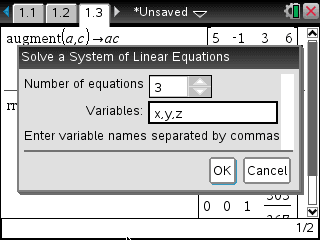
      03-24-2016 Image013-32p.png
       
    3. 식을 입력합니다. 
      03-24-2016 Image014-32p.png

     

    Attached file
    03-24-2016 Image004-32p.png 2.7KB 11803-24-2016 Image005-32p.png 2.9KB 12203-24-2016 Image006-32p.png 2.7KB 10203-24-2016 Image007-32p.png 2.2KB 10603-24-2016 Image010-32p.png 3.2KB 12103-24-2016 Image011-32p.png 5.4KB 12603-24-2016 Image012-32p.png 5.6KB 13403-24-2016 Image013-32p.png 4.4KB 9803-24-2016 Image014-32p.png 3.5KB 123linear_equation3.tns 1.4KB 178
    이 게시물을..
    N
    0
    0
    • [TI-nspire] 삼각함수의 변환 명령 - ▶cos, ▶sin세상의모든계산기
    • [TI-nspire] [업데이트] OS version 4.5세상의모든계산기
    • 세상의모든계산기 25
      세상의모든계산기

      계산기는 거들 뿐
      혹은
      계산기를 거들 뿐

    세상의모든계산기 님의 최근 글

    높아질수록 좁아지는 시야에 대하여 - written by ChatGPT 659 2026 02.12 내가 올해 몇살이더라? (내 나이 계산기) 476 2026 02.11 AGI 자기 거버넌스 구조와 인간-AGI 관계 모델 (written by GEMINI & GPT) 737 1 2026 01.30   AI 시대, '기본소득'을 넘어 '기여소득'으로: 새로운 사회 계약을 향한 제언 - Written by Gemini 630 1 2026 01.28 쌀집계산기로 선형 연립방정식 계산하기 - 크래머/크레이머/크라메르 공식 적용 342 2 2026 01.18

    세상의모든계산기 님의 최근 댓글

    감사합니다. 주말 잘 보내세요. 2026 03.06 [fx-570 ES] 과학 상수를 이용한 계산에서 에러 발생 상황 https://kin.naver.com/qna/detail.naver?d1id=11&dirId=1118&docId=492235162&page=1&answerNo=1    vs  2026 03.01 과학상수를 이용한 계산 중 자릿수 한계로 인한 에러 발생 가능성 https://allcalc.org:443/board_calculators/6925#comment_57029 2026 03.01 기본 어댑터 MODEL : AD0301-1202500GB INPUT : 100~240V, 50~60Hz, 0.8A Max OUTPUT : 12.0V, 2.5A, 30.0W   ㄴ 측정시 플러그 외경/내경 : 5.5mm / 2mm  2026 02.15 엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10
    글쓴이의 서명작성글 감추기 

    댓글2

    • Profile 0
      세상의모든계산기
      2016.03.24 - 19:06 2016.03.24 - 19:05 #16424

      Gauss-Zeidel (반복)법을 이용한 풀이

      http://www.allcalc.org/8143

      댓글
    • Profile 0
      세상의모든계산기
      2018.08.14 - 08:40 2018.08.14 - 08:40 #23848

      ​복소 연립 방정식도 같은 방법으로 풀 수 있습니다.

      TI-Nspire CX CAS Student Software_2018-08-14_08-46-48.png

      Attached file
      TI-Nspire CX CAS Student Software_2018-08-14_08-46-48.png 9.7KB 136
      댓글
    • 댓글 입력
    • 에디터 전환
    댓글 쓰기 에디터 사용하기 닫기
    • view_headline 목록
    • 14px
    • [TI-nspire] 삼각함수의 변환 명령 - ▶cos, ▶sin
    • [TI-nspire] [업데이트] OS version 4.5
    • 목록
      view_headline
    2
    × CLOSE
    전체 nspire 139 89 11 86, 84, 83 7 BA II Plus 8 공통 1
    기본 (168) 제목 날짜 수정 조회 댓글 추천 비추
    분류 정렬 검색
    • 48 nspire [TI-BASIC] Program 과 Function 의 차이
    • 세상의모든계산기 2015.09.27 - 15:47 1612 1
    • 출처 : http://tibasicdev.wikidot.com/nspire Program Function Return a result? 결과를 반환하는가? No Yes Can be used in an expression? 수식내에서 사용 가능한가? No Yes Can run in applications other than Calculator? 계산기 이외의 어플에서 실행가능한가? No Yes Can use all the commands? 모든 명령어를 사용할 수 있나? Yes No Can use multiple variable types? 다중 변수타입을 사용할 수 있는가? Yes Yes Can access global variables? 전역 변수에 접근할 수 있는가? Yes Yes Can modify and create global variables...
    • 47 nspire angle() 함수 사용 방법
    • 세상의모든계산기 2022.01.07 - 11:59 1034
    • Reference Guide 발췌 angle(Exprl) ⇒ expression Returns the angle of the argument, interpreting the argument as a complex number. 인수를 복소수로 해석하여, 인수의 각도를 반환합니다. Note: All undefined variables are treated as real variables. 참고: 정의되지 않은 모든 변수는 실수 변수로 취급됩니다. angle(List1) ⇒ list angle(Matrix1) ⇒ matrix Returns a list or matrix of angles of the elements in List1 or Matrix1, interpreting each element as a complex number that represents a two-dimensional rectang...
    • 46 nspire [TI-nspire] 벡터 사이 각도(사잇각) 구하기
    • 세상의모든계산기 2017.11.01 - 11:53 2503 1
    • 문제 : 두 벡터 사이의 사잇각을 구하여라. V1=[-1 2], V2=[4 -1] 풀이 :
    • 45 nspire [TI-Nspire 시리즈] 정보(글) 및 링크 모음
    • 임시닉네임 2021.08.29 - 16:27 2318
    • 0. 종류 TI-Nspire는 크게 네 종류로 나눌 수 있습니다. 크게 나누면 클릭패드가 탑재된 TI-Nspire 라인업, 터치패드가 탑재된 TI-Nspire 라인업, TI-Nspire CX 라인업, TI-Nspire CX II 라인업으로 나뉩니다. TI-Nspire 라인업은 모두 흑백 액정을 탑재했으며, 키패드가 CX/CX II 라인업과 동일하면 터치패드 탑재 모델입니다. 모든 라인업은 CAS 지원 여부에 따라 다시 두 가지로 나뉘며, 중화인민공화국/유럽 등 국가/지역별 커스텀되어 판매되는 모델도 있습니다. School Property 표시가 있고, 황색이 들어간 학교용도 존재합니다. 주...
    • 44 nspire [kArmTI] : TI-nspire 에뮬레이터
    • 세상의모든계산기 2015.02.28 - 13:06 4335 3
    • 1. 설명 PC-Windows용 TI-nspire 계산기 에뮬레이터 입니다. 2. PC 용 TI-nspire (CAS) Student Software 와 차이 (장점) 시리얼 번호가 필요 없어서 여러 PC에 설치해 사용할 수 있습니다. 여러 버전의 OS를 설치하여 자유롭게 사용해 볼 수 있습니다. PC용 버전은 계산기 버전과 차이점이 조금 있지만, 에뮬레이터는 완전 동일하게 작동합니다. 실물 계산기보다는 빠르고, PC버전보다는 조금 느린 것 같습니다. (단점) 아직 기능이 완벽하지 않아서 터치패드 작동은 조금 불편합니다. 파일 관리가 조금 불편합니다. 3. 에뮬레이터 다운로...
    • 43 nspire [TI-nspire] 조각함수 Piecewise Function 의 입력
    • 세상의모든계산기 2016.09.06 - 14:21 2572 2
    • 1. 조각함수란? 함수의 조합?으로, 구간에 따라 서로 다른 함수가 적용되는 함수를 지칭합니다. 상세한 내용은 위키 등을 참고하시기 바랍니다. 위키 : https://en.wikipedia.org/wiki/Piecewise 2. 조각함수 입력 방법1 : 템플릿 이용 □,□ 의 앞쪽에 수식을 넣고, 뒷쪽에 구간(interval) 을 넣습니다. 방법2 : 함수 이용 piecewise(Expr1 [,cond1 [,Expr2 [,cond2 [, ... ]]]]) 상세한 내용은 설명서를 참고하세요. (그렇게까지 상세하진 않습니다) 방법3 : 제약 연산자(|) 이용 제약연산자를 이용해 함수를 입력하면, 자동으로 piecewise...
    • 42 nspire TI-Nspire™ CX II (CAS) 출시
    • 세상의모든계산기 2019.03.08 - 00:54 5432 16
    • 공홈 하드웨어 스펙 소개 TI-Nspire™ CX II and CX II CAS graphing calculator specifications General Screen Storage 90+ MB storage memory 64 MB operating memory Color Backlit display Power TI Rechargeable Battery (included) USB port for computer connectivity Size 320 x 240 pixels (3.2" diagonal) Connector USB cable included Resolution 125 DPI; 16-bit color https://education.ti.com/en/products/calculators/graphing-calculators/ti-nspire-cx-ii-cx-ii-cas 기존 CX 모델과 비교하면... http://www.allcalc.org...
    • 41 nspire [TI-nspire] 입력한 내용의 수정방법
    • 세상의모든계산기 2016.09.06 - 13:50 6272 3
    • 1. 계산 전 수정하기 계산 전에는 '방향키 or 단축키 or 터치패드' 를 이용하여 수정하고 싶은 위치로 커서를 옮기고, 내용을 수정하시면 됩니다. 입력시 (덮어씌워지지 않고) 기존 입력내용 사이에 삽입되기 때문에, 필요없는 것은 【del】 키로 지우셔야 합니다. 2. 계산 후 수정하기 이미 계산되어 Entry (History) 에 등록된 내용은 절대 수정할 수 없습니다. (History 삭제만 가능) History 에 저장되어 있는 계산식은 언제라도 다시 불러올 수 있습니다. 하나의 입력식 전부를 불러올 때 계산이 완료되어 Histoty 에 등록된 상태 방...
    • 40 nspire TI 포럼에 오신걸 환영합니다.
    • 세상의모든계산기 2015.01.13 - 15:46 1303 1
    • TI 포럼입니다. TI는 Texas Instruments 라는 회사로 계산기 시장을 주름잡는 전통있는 회사입니다. 89titanium 뿐 아니라 TI-nspire에서도 좋은 평가를 받고 있습니다. 미쿡 제품답게 조금은 투박한 디자인을 담고 있는데, 디자인 측면에서는 확실히 HP에게 밀리는 모양새입니다
    • 39 nspire [TI-nspire] nsolve() : 솔브 함수, 방정식의 해를 구하는 함수
    • 세상의모든계산기 2015.10.27 - 08:58 7689 2
    • 1. 개요 nsolve() 함수는 solve 함수의 일종입니다. 방정식이나 부등식의 실수해(real solutions)를 추정하여 반환하는 함수입니다. 결과가 딱 떨어지는 일반 함수들과는 달라서 사용에 조금 주의를 할 필요가 있습니다. CAS 기종에서는 solve(), csolve(), nsolve(), linsolve() 함수를 모두 내장하고 있으므로, 필요에 따라 적당한 것을 사용합니다. 하지만 Non-CAS 기종에서는 nsolve() 와 linsolve() 뿐이므로, 어쩔 수 없이 nsolve() 를 주로 사용합니다. 2. 사용 방법 ⓐ nsolve(Equation, Var[=Guess]) ⇒ number or error_string ⓑ n...
    • 38 nspire [TI-nspire] nspire Series 계산기 소개 및 비교
    • 세상의모든계산기 2015.01.15 - 09:55 7041 5
    • 1. 소개 TI-nspire 는 2007년 처음 선보인 TI 의 주력 계산기종입니다. 일반인들에게 판매되는 공학용 계산기중 가장 비싼 녀석이고, 비싼 만큼 강력하긴 합니다만, 비싸도 너무 비싼 감이 있습니다. (시장 특유의 독과점 및 충성도?에 따른 것으로 보입니다.) 2. 분류 Clickpad ▶ Touchpad ▶ CX(칼라) 순서로 버전업 되었습니다. 각각 CAS 기능이 있는 버전과, 기능이 빠진(Non-CAS) 버전 두가지로 출시되었으니, 총 6종으로 분류할 수 있습니다. (세부적으로 더 나뉘어집니다만, 별 의미는 없습니다.) Non-CAS CAS CX : 액정이 칼라 TI-N...
    • 37 nspire [TI-nspire] 함수의 점근선 구하기 : Analyze Graph - Asymptotes
    • 세상의모든계산기 2015.11.07 - 14:12 3074
    • 1. 점근선이란? [네이버 지식백과] 점근선 [asymptote, 漸近線] (두산백과) 무한분지(無限分枝)를 가지는 곡선에 있어서 동점(動點)이 그 분지에 따라 원점에서 멀어질 때, 그 점에서 한 정직선(定直線)에의 거리가 0에 가까워질 때의 정직선을 말한다. 수평 점근선 : x 가 +∞ 또는 -∞로 갈때 한없이 가까워지는 수평선이 수평 점근선 수직 점근선 : 함수(y)가 어떤 영향도 받지 않으면서 값이 계속 커질 때 y축에 평행한 수직선에 가까워지면 그 수직선이 수직 점근선 사선 점근선 : 점근선이 x축, y축에 평행하지 않은 경우 2. TI-nspire...
    • 36 nspire [TI-nspire] 전원 Power On & Off / 대기 모드 Hibernate / 딥 슬립 Deep Sleep
    • 세상의모든계산기 2019.01.21 - 11:18 4934
    • 1. 전원 On / Off 【on】 버튼을 눌러 기기를 켭니다. ├ 기기가 Stanby 상태일 때는 바로 화면이 바로 켜집니다. ├ 로고 화면(Progress Bar)이 나타나는 것은 OS가 새로 로딩됨을 의미합니다. └ 최초 실행이라면 이후 언어와, 폰트크기를 묻는 창이 나타납니다. 【ctrl】【on】 버튼(=off)을 눌러 기기를 끕니다. (Standby 모드로 진입) ├ 마지막 사용중이던(Current) 모든 설정과 메모리 내용들은 (다시 켤 때) 그대로 유지됩니다. └ 단, Reset 할 경우 Document로 저장하지 않은 설정과 내용은 사라집니다. 2. 끄기 Off (Standby / APD /...
    • 35 nspire [TI-nspire] 내장 과학 상수 값 Constants and Values
    • 세상의모든계산기 2018.12.27 - 12:20 2794 2
    • 1. 내장 과학 상수와 그 값 TI-nspire CX CAS (OS v4.5) 에는 아래의 과학상수가 내장되어 있습니다. Constant Name Value _c Speed of light 299792458 _m/_s _Cc Coulomb constant 8987551787.3682 _m/_F _Fc Faraday constant 96485.33289 _coul/_mol _g Acceleration of gravity 9.80665 _m/_s2 _Gc Gravitational constant 6.67408E-11 _m3/_kg/_s2 _h Planck's constant 6.626070040E-34 _J _s _k Boltzmann's constant 1.38064852E-23 _J/_¡K _m0 Permeability of a vacuum 1.2566370614359E-6 _N/_A2 _mb Bohr magneton 9.27400999...
    • 34 nspire [TI-nspire] operating system not found. Install OS now. 운영체제 재설치
    • 세상의모든계산기 2015.12.01 - 21:16 2692 2
    • TI‐nspire CAS Touchpad Operating System not found. Install OS now. Computer to Unit Transfer 계산기의 화면이 이렇게 바뀌고 아무것도 되지 않는다면, 계산기를 전반적으로 관리하는 OS 가 corrupted(오염)된 상황입니다. 단지 소프트웨어의 문제라면 사용자의 힘으로 문제가 깔끔하게 해결될 수 있겠지만, 하드웨어의 문제 때문에 발생한 상황이라면, 사용자의 힘으로 해결이 안될 수도 있고, 해결된다고 해도 재발할 가능성이 있습니다. 따라서, 무상 AS 기간이 남아있다면 구입처나 수입업체에 문의를 해보시고, 제품을 교체를 받...
    • 33 nspire [TI-nspire] 삼각함수의 변환 명령 - ▶cos, ▶sin
    • 세상의모든계산기 2015.12.29 - 20:55 6658 1
    • 1. 주의사항 삼각함수의 표시 변환 명령인 ▶cos ▶sin 은 입력줄의 맨 마지막에 위치해야 합니다. 각도설정은 무조건 radian 으로 해두어야 합니다. 모든 sin 을 cos으로 (혹은 반대로) 바꾸는 명령이 아닙니다. 원하는 결과형식이 아닌경우 tcollect(), texpand() 명령을 사용해 보세요. 정확하게 원하는 꼴로 바뀌지 않을 확률이 더 많습니다. 적당한 선에서 만족하시고, 손으로 최종정리하는 쪽이 정신건강에 좋습니다. 2. 사용 예시 단축 메뉴 【menu】【3】【A】【3】【4】 (▶sin) 【menu】【3】【A】【3】【5】 (▶cos)
    • nspire [TI-nspire] 연립방정식 풀기 - 역행렬 / RREF / linsolve
    • 세상의모든계산기 2016.03.24 - 18:50 22014 2
    • 1. 연립방정식 연립방정식 및 그 풀이방법에 대해서는 아래 링크를 확인해주세요. http://www.allcalc.org/14534 아래에서는 행렬을 이용해서 연립방정식 예제를 풀어보도록 하겠습니다. 5x1 - x2 + 3x3 = 6 4x1 + 7x2 + x3 = 2 2x1 + 3x2 + 10x3 = 9 2. 역행렬 이용 【9】오른쪽의 템플릿 버튼을 눌러서 템플릿창을 띄웁니다. 3×3 이상의 행렬은 3칸짜리를 선택 행과 열을 입력 행렬의 각 칸에 요소를 입력하고 a에 저장 우변의 상수항은 c에 저장 변수에 저장하지 않아도 계산은 가능은 하지만, 재사용할 때 편리하게 사용하려면 변수에 ...
    • 31 nspire [TI-nspire] [업데이트] OS version 4.5
    • 세상의모든계산기 2017.09.30 - 14:36 1546
    • 업데이트 관련 페이지 https://education.ti.com/en/product-resources/whats-new 업데이트 내용 설명 PDF https://education.ti.com/-/media/ti/files/resources/whats-new/whats-new-ti-nspire-cx-release-history.pdf?la=en&revision=c4461eb4-4fed-4b60-aebb-3e80bd47b5f6&modified=20170829154516&hash=362CB44A183E90ADDB73B220B2A1960C2109AC91 1. v4.5 변동사항 Unit Conversion Assistant Constants and Values Programming Editor Programming Updates : DispAt, getKey 2. v4.4 변동사항 Restricted Domains Sequence Graphing ...
    • 30 nspire [TI-nspire] Iteration, Gauss-Seidel 가우스-자이델 반복법으로 연립방정식 풀기 (행렬X)
    • 세상의모든계산기 2015.10.08 - 11:14 5082
    • http://www.allcalc.org/16404 연립방정식을 푸는 방법으로서 역행렬, RREF, linsolve() 등을 이용한 일반적인 방법 이외에 가우스-자이델 Gauss-Seidel 반복법을 이용한 풀이법를 소개합니다. 1. 문제 다음 연립방정식을 "Gauss-Seidel 법"으로 풀어라. 5x1-x2+3x3=64x1+7x2+x3=22x1+3x2+10x3=9 2. 풀이 a, b, c 변수에 0을 저장합니다. (x1, x2, x3 대식 a,b,c 를 사용합니다) (값이 비어있을 경우에 "Error: Circular definition" 이 발생할 수 있습니다) 각 식을 각각 a, b, c 에 대한 식으로 정리하고, ":" 기호를 이용해서 한 라인에...
    • 29 nspire [TI-nspire] [프로그래밍] 몬테 카를로 방법 예시 - Monte Carlo Method
    • 세상의모든계산기 2017.11.05 - 20:33 1134 3
    • 1. 몬테 카를로 방법이란? https://ko.wikipedia.org/wiki/%EB%AA%AC%ED%85%8C%EC%B9%B4%EB%A5%BC%EB%A1%9C_%EB%B0%A9%EB%B2%95 2. 프로그래밍 예시 - pi 근사값 구하기 :Define mc_pi(r,n)= :Prgm :Local point :For j,1,r :0→inner :For i,1,n : rand(2)→point : If point[1]^(2)+point[2]^(2)≤1 Then : inner+1→inner : EndIf :EndFor :approx(((inner)/(n))*4)→thispi :Disp "#",j,"/",r,", pi=",thispi :augment(pilist,{thispi})→pilist :EndFor :EndPrgm 1라운드 당 n회 random 하게 point 를 생성하고 원 내부의 점(inner point)인...
    • 1 2 3 4 5 6 7 8 9
    • / 9 GO
    • TI
    • 세상의모든계산기
    • 사업자등록번호 703-91-02181
    • 세모계 all rights reserved.